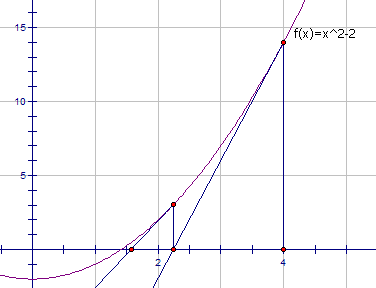
任意一点$x_0, f(x_0)$的切线斜率为$2x_0$
根据切线和x轴形成的三角形
可求得切线和x轴交点坐标为$(x_0 - \frac{f(x_0)}{2x_0})$
再将交点带入计算公式,递归下去就能无限接近解了
class Solution {
int s;
int mySqrt(int x) {
s = x;
if(x==0) return 0;
return ((int)(sqrts(x)));
}
double sqrts(double x){
double res = (x + s / x) / 2;
if (res == x) {
return x;
} else {
return sqrts(res);
}
}
}可以把这个转化成01问题,找第一个1前面的
假设数组
0, 1, 2, 3, 4...
0, 1, 4, 9, 16...
比如对于10,不就是找最后一个<=它的,也就是第一个>它的前面一个么!
这个边界条件把我整麻了
class Solution {
public:
int mySqrt(int x) {
// double的就可以当成连续的了
// 不用当成数组处理
double head = 0, tail = x, mid;
tail += 1;
// 固定次数100次一定能将问题规模缩小到常数级别
for (int i = 0; i < 100; i++) {
mid = (head + (tail - head) / 2);
if (mid <= x / mid) head = mid;
else tail = mid;
}
return head;
}
};class Solution {
public:
int mySqrt(int x) {
double l = 0, r = x, mid;
r += 1;
for (int i = 0; i < 100; i++) {
mid = l + (r - l) / 2.0;
// 这里就不用处理l = mid - 1了
// 因为最后l r会无限接近
if (mid * mid > x) r = mid;
else l = mid;
}
return floor(l);
}
};class Solution {
public:
int binary_search(vector<int> &nums, int t) {
int l = 0, r = nums.size() - 1, mid;
// 但是这种写法会有一个bug
// 比如[1,3,5,6]插入7 这个返回的就是-1
// 当在数组中找不到插入位置的时候说明元素大于数组中的所有元素!
// 返回num.size()
while (r - l > 3) {
mid = (l + r) >> 1;
// 其实下面这一行有点多余了
// 因为最后target一定是在(l, r)区间内的
if (nums[mid] == t) return mid;
if (nums[mid] < t) l = mid + 1;
else r = mid;
}
for (int i = l; i <= r; i++) {
if (nums[i] >= t) return i;
}
return nums.size();
}
int searchInsert(vector<int>& nums, int target) {
return binary_search(nums, target);
}
};编程技巧:对下标排序
class Solution {
public:
int binary_search(vector<int> &nums, vector<int> &ind, int l, int t) {
int r = ind.size() - 1, mid;
while (l <= r) {
mid = (l + r) >> 1;
if (nums[ind[mid]] == t) return mid;
if (nums[ind[mid]] < t) l = mid + 1;
else r = mid - 1;
}
return -1;
}
vector<int> twoSum(vector<int>& nums, int target) {
// 编码技巧:对数组下标进行排序
// 因为最后要返回数组下标
vector<int> ind(nums.size());
vector<int> ret(2);
for (int i = 0; i < ind.size(); i++) ind[i] = i;
sort(ind.begin(), ind.end(),
[&](int i, int j) { return nums[i] < nums[j]; });
// 遍历ind数组 就相当于从小到大遍历nums了
for (int i = 0; i < ind.size(); i++) {
int val = nums[ind[i]];
// 传入存val 存ind的数组 起始位置和待查找值
int j = binary_search(nums, ind, i + 1, target - val);
if (j == -1) continue;
// 找到了a b
// 但是题目要求按大小顺序存储a b
int a = ind[i];
int b = ind[j];
if (a > b) swap(a, b);
ret[0] = a;
ret[1] = b;
}
return ret;
}
};class Solution {
public:
// 01 模型
// >= x 的是1
// 所以nums[mid] >= x的时候不能越过mid
int binary_search(vector<int> &nums, int x) {
int l = 0, r = nums.size() - 1, mid;
while (r - l > 3) {
mid = (l + r) >> 1;
if (nums[mid] >= x) r = mid;
else l = mid + 1;
}
for (int i = l; i <= r; i++) {
if (nums[i] >= x) return i;
}
return nums.size();
}
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> ind(nums.size());
for (int i = 0; i < ind.size(); i++) ind[i] = i;
vector<int> ret(2);
ret[0] = binary_search(nums, target);
if (ret[0] == nums.size() || nums[ret[0]] != target) {
ret[0] = ret[1] = -1;
return ret;
}
// 因为数组是有序排列的
// 所以找大于tar的第一个的前一个不就是tar的最后一个
ret[1] = binary_search(nums, target + 1) - 1;
return ret;
}
};这个抽象的能力很重要 也很有意思 难的其实不是二分 而是二分当成思想抽象
理解完题意
就是左边找一些数,右边找一些数
他们的和等于x
也就是我们要在左边找一个
然后二分在右边找一个?
N0!数组不是有序的
而且呢又不是找两个数
这时候就想到了前缀和
上面左边的一些数刚好可以用左边的前缀和数组替代
右边的数用右边开始的前缀和
并且数组中任意元素>=0
前缀和数组一定是有序的
这样就能左找一个 右找一个实现二分了
class Solution {
public:
//前后两个前缀和
int binary_search(vector<int> &nums, int x) {
int head = 0, tail = nums.size() - 1, mid;
while (head <= tail) {
mid = (head + tail) >> 1;
if (nums[mid] == x) return mid;
if (nums[mid] < x) head = mid + 1;
else tail = mid - 1;
}
return -1;
}
int minOperations(vector<int>& nums, int x) {
vector<int> suml(nums.size() + 1);
// suml[0] = 0
vector<int> sumr(nums.size() + 1);
suml[0] = sumr[0] = 0;
// 比如去nums[0]就是一次操作
// 所以要把nums[0]放到suml[1]上去 这样就能直接对应了
for (int i = 0; i < nums.size(); i++) suml[i + 1] = suml[i] + nums[i];
for (int i = nums.size() - 1; i >= 0; i--) sumr[nums.size() - i] = sumr[nums.size() - i - 1] + nums[i];
int ans = -1;
for (int i = 0; i < suml.size(); i++) {
int j = binary_search(sumr, x - suml[i]);
if (j == -1) continue;
// i + j是选择的元素总数量
// 也就是左右区间出现了重复!
if (i + j > nums.size()) continue;
if (ans == -1 || ans > i + j) ans = i + j;
}
return ans;
}
};思路:
对供暖器数组排序
遍历房屋数组,求出每个房屋离他最近供暖器的距离
最所有的距离取MAX
那么现在问题来了,怎么求离供暖器的距离呢?
假设当前房屋位置为x
取暖器数组为[a1, a2, a3, a4]
x落在[a3, a4]之间
那么看x离哪个最近不就得了
转化到二分上就是找第一个>= x的!
和他前面那个取最小值 01模型
class Solution {
public:
// 01
int binary_search(vector<int> &nums, int x) {
int l = 0, r = nums.size() - 1, mid;
while (l < r) {
mid = (l + r) >> 1;
if (nums[mid] >= x) r = mid;
else l = mid + 1;
}
// 此时l == r
// 但是不一定nums[l] >= x
// 因为如果l == r == nums.size() - 1
// 说明数组最大的元素,最后一个元素都<x
// 也就是在合法的范围内返回第一个 >= x的位置
// 或者返回 < x 但是离他最近的位置 (所以下面a用了abs)
return l;
}
int findRadius(vector<int>& houses, vector<int>& heaters) {
sort(heaters.begin(), heaters.end());
int ans = 0;
for (auto x : houses) {
int y = binary_search(heaters, x);
int a = abs(heaters[y] - x);
// y > 0? 如果>0才有前一个元素!
// 否则给他个比a大的值就行
// 就是最后选a的意思
int b = (y ? abs(heaters[y - 1] - x) : a + 1);
ans = max(ans, min(a, b));
}
return ans;
}
};这个题可以帮我们深入体会二分分的是区间!
待查找值一定要在区间内!
简单来说 数组表现为下图的形式
整个区间并不是递增的
这就需要分情况了
- 确定mid在左区间还是右区间 (mid < r -> 在右侧单调区间)(mid > l -> 在左侧单调区间)
- 因为二分一定要在递增的区间才能做的,所以要根据上面的两种情况继续找递增区间
如下图所示
if (mid < r) -> 右侧
if (r > mid && mid < x) -> 右边递增区间 l = mid + 1;
else r = mid - 1; -> x在左侧
if (mid > l) -> left
if (l > mid && mid > x) -> 左边递增区间 r = mid - 1;
else l = mid + 1; -> x在右侧
Q:else 里面的不就又无序了吗? 跟人感觉不一定有序
因为这个题重点是缩小了区间的范围 缩小了问题的规模
而且mid每次调整都在查找范围内 所以又无序的也无妨!
class Solution {
public:
bool search(vector<int>& nums, int target) {
// 两头的值 == target 就是找到了
if (nums[0] == target || nums[nums.size() - 1] == target) return true;
int l = 0, r = nums.size() - 1, mid, head, tail;
// 先去掉头尾 == nums[0]的值
// 为的是让nums[l] > nums[r]
// 方便进行边界条件判断
while (l < nums.size() && nums[l] == nums[0]) ++l;
while (r >= 0 && nums[r] == nums[0]) --r;
// head和tail分别记录左右区间的位置
head = l, tail = r;
while (l <= r) {
mid = (l + r) >> 1;
if (nums[mid] == target) return true;
// 在右边的递增区间
if (nums[mid] <= nums[tail]) {
// 正是前面的++l --r 才能用 <= 号
if (target <= nums[tail] && target > nums[mid]) {
l = mid + 1;
} else {
r = mid - 1;
}
// 在左边的递增区间
} else {
if (nums[head] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
}
}
return false;
}
};二分分的是问题规模
每次缩小查找区间
缩的就是问题规模!
此题的问题规模是什么呢?
(当然可以参考归并排序)
不妨假设是两个数组中找第k大的问题
现在有a[], b[]
但是a[k / 2] < b[k / 2]
因为是找第k大么,假设取a中的 k / 2个
可得出剩下的k / 2将在a的剩余部分和b的前[k / 2]取
严谨的证明:
求a[k / 2]元素的排名 也就是红色方块
首先a前面它有k / 2 - 1个
最大排名就是k - 1个 不是第k个
也就是说 a 数组的红色部分全是前k个元素,并且不包含第k个
并且数量是 k / 2
去掉这k / 2个之后 剩下的去哪里找呢?
那当然是a右侧(比a[k / 2]大)或者b左侧
但是处理边界条件比较复杂
class Solution {
public:
// 参数说明 nums1 nums2 1的起始查找位置 2的起始查找位置 第k大
double findK(vector<int> &nums1, vector<int> &nums2, int i, int j, int k) {
// 1 2都为空了 就返回另一个数组排名k的
// i j 是 1 2的起始位置
if (i == nums1.size()) return nums2[j + k - 1];
if (j == nums2.size()) return nums1[i + k - 1];
// 取一个就取1 2里最小的
if (k == 1) return min(nums1[i], nums2[j]);
// a在(k / 2)和(i ~ n)中取最小的
// 如果k / 2 > 1.size()就取(i ~ n) 也就是剩余的元素
int a = min(k >> 1, (int)nums1.size() - i);
// 还剩k - a个 同时保证b中不取光
int b = min(k - a, (int)nums2.size() - j);
// 要维护a + b == k的关系
a = k - b;
// 如果1 < 2 就放弃1已经查找的部分
// 去1右边和b中找
if (nums1[i + a - 1] < nums2[j + b - 1]) {
return findK(nums1, nums2, i + a, j, k - a);
} else {
return findK(nums1, nums2, i, j + b, k - b);
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), m = nums2.size();
int mid = (n + m + 1) >> 1;
// 细节 + 1防止奇数
// 因为对于[1, 2, 3]来说我们想取第2大
// 但是n + m >> 1 = 1 这时 + 1就可以解决
double a = findK(nums1, nums2, 0, 0, mid);
// 奇数 中位数就一个
if ((n + m) % 2) return a;
// 偶数中位数有两个要取平均值
double b = findK(nums1, nums2, 0, 0, mid + 1);
return (a + b) / 2;
}
};