242
class Solution {
public:
bool isAnagram(string s, string t) {
if (s.size() != t.size()) return false;
if (s.size() == t.size() && s.size() == 1) return s[0] == t[0];
int mark_s[26] = {0}, mark_t[26] = {0};
for (auto x : s) {
mark_s[x - 'a'] += 1;
}
for (auto x : t) {
mark_t[x - 'a'] += 1;
}
for (int i = 0; i < 26; i++) {
if (mark_s[i] != mark_t[i]) return false;
}
return true;
}
};454
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
// h为 1 2数组任意两项的和 -> 和出现次数的映射
unordered_map<int, int> h;
for (auto x : nums1) {
for (auto y : nums2) {
h[x + y] += 1;
}
}
int ans = 0;
// 因为和 == 0
// 所以x + y + z + w == 0
// 也就是如果存在四元组
// 就能在哈希表中找到 0 - x - y(即z + w)
// 因为可能不止一个 所以出现次数正好就是元组总数
for (auto x : nums3) {
for (auto y : nums4) {
if (h.find(0 - x - y) != h.end()) ans += h[0 - x - y];
}
}
return ans;
}
};用拉链法实现,并且对链表采用尾插的办法。
class Node {
public :
Node (int key = 0, Node *next = nullptr) : key(key), next(next) {}
int key;
Node *next;
void insert_after(Node *node) {
node->next = this->next;
this->next = node;
return ;
}
void remove_after() {
if (this->next == nullptr) return ;
Node *p = this->next;
this->next = p->next;
delete(p);
return ;
}
private :
};
class MyHashSet {
public:
vector<Node> data;
MyHashSet() : data(100) { }
// 怎么设计hash函数无所谓
// 本题的考点不在这里
// 或者说几乎所有的哈希表的题考点都不在这里
// 只要把他转化为非负数即可
int hash(int key) { return key & 0x7fffffff; }
void add(int key) {
if (contains(key)) return ;
// 获取hash值
int ind = hash(key) % data.size();
data[ind].insert_after(new Node(key));
return ;
}
void remove(int key) {
int ind = hash(key) % data.size();
Node *p = &data[ind];
// 走到待删除节点的前一个
while (p->next && p->next->key != key) p = p->next;
p->remove_after();
return ;
}
bool contains(int key) {
int ind = hash(key) % data.size();
Node *p = data[ind].next;
while (p && p->key != key) p = p->next;
// 走完while循环 说明要么找到了等于key的节点p 要么走到了最后一个
return p != nullptr;
}
};我们知道data[ind]就是找到了data中的链表的起始点
但是这个节点是不存val的(因为采用的是尾插法)
并且删除节点要走到待删除节点的前一个节点才行!
所以删除的时候不能先走一步,要指向data[ind](万一删除仅有的一个)
而查找的时候肯定是要找值存在的
在705的基础上多了一个k-v的映射关系
这和我们如何实现哈希,拉链法是没关系的哈
依然采用尾插尾删法
class Node {
public :
Node(int k = 0, int v = 0, Node *n = nullptr) : k(k), v(v), n(n) { }
int k, v;
Node *n;
void insert(Node *node) {
node->n = this->n;
this->n = node;
return ;
}
void _remove() {
if (this->n == nullptr) return ;
Node *p = this->n;
this->n = p->n;
delete(p);
return ;
}
private :
};
class MyHashMap {
public:
vector<Node> data;
MyHashMap() : data(100) { }
int hash(int k) { return k & 0x7fffffff; }
void put(int key, int value) {
int ind = hash(key) % data.size();
Node *p = &data[ind];
// 因为put的要求是如果存在k-v 就更新v
// 在链表中找key
while (p->n && p->n->k != key) p = p->n;
// 走到这里说明p->n->k == key了!
// 也就是我们要更新下一个节点的v
if (p->n) p->n->v = value;
// 不存在才插入
else p->insert(new Node(key, value));
return ;
}
// 剩下俩都和上面逻辑一样
int get(int key) {
int ind = hash(key) % data.size();
Node *p = data[ind].n;
while (p && p->k != key) p = p->n;
return p ? p->v : -1;
}
void remove(int key) {
int ind = hash(key) % data.size();
Node *p = &data[ind];
while (p->n && p->n->k != key) p = p->n;
p->_remove();
return ;
}
};LRU是一种数据的置换算法 就是在有限的空间,数据多于有限的空间了
怎么用一种算法来置换数据呢?
本题采用的就是LRU(最近最久未使用)
这也要求我们在更新和插入的时候,要对节点特殊处理
更新的时候,证明此k-v被访问过了,要删除它,再把它插到tail后面
插入的时候,如果存在k-v,就相当于要更新他(先删除它,再尾插)
如果不存在就可以直接尾插了
如果插入完成节点数量 > 存储空间了 就删除第一个节点
哈希链表底层是链表 用哈希表来索引
实现的时候引入了虚拟头尾节点
并且改进成了双向链表
class Node {
public :
Node (int key = 0, int value = 0, Node *next = nullptr, Node *pre = nullptr) : key(key), value(value), next(next), pre(pre) {}
int key, value;
Node *next, *pre;
// 设计remove this比较好实现
Node *remove_this() {
if (this->pre) this->pre->next = this->next;
if (this->next) this->next->pre = this->pre;
this->next = nullptr, this->pre = nullptr;
return this;
}
// this 前一位插入 也是比较好实现的
void insert_pre(Node *node) {
node->next = this;
node->pre = this->pre;
if (this->pre) this->pre->next = node;
this->pre = node;
return ;
}
};
class HashList {
// 虚头 + 虚尾
public :
int capacity;
Node head, tail;
unordered_map<int, Node *> data;
HashList(int capacity) : capacity(capacity) {
head.next = &tail;
tail.pre = &head;
}
void put(int key, int value) {
// 如果存在key 就要更新value
// 并且代表最近使用过 要把这个节点删除
// 并且在尾部插入
if (data.find(key) != data.end()) {
data[key]->value = value;
data[key]->remove_this();
} else {
data[key] = new Node(key, value);
}
tail.insert_pre(data[key]);
if (data.size() > capacity) {
data.erase(data.find(head.next->key));
delete head.next->remove_this();
}
return ;
}
int get(int key) {
// 没找到key
if (data.find(key) == data.end()) return -1;
// 删除原来的节点,然后尾部插入新的
data[key]->remove_this();
tail.insert_pre(data[key]);
return data[key]->value;
}
};
class LRUCache {
public:
HashList h;
LRUCache(int capacity) : h(capacity) {}
int get(int key) {
return h.get(key);
}
void put(int key, int value) {
return h.put(key, value);
}
};题意就是找长度 == 10且出现次数 > 1的字串
哎 这也难怪不就可以建立起一个字串 -> 出现次数的映射了么!
class Solution {
public:
vector<string> findRepeatedDnaSequences(string s) {
unordered_map<string, int> h;
// 所有的字串放到哈希表中
// 字串 -> 字串出现次数的映射
// I是循环的最后一个位置
// 每次从0~I循环
// 直接大暴力就行
for (int i = 0, I = s.size() - 9; i < I; i++) {
// 字串出现次数 += 1
h[s.substr(i, 10)] += 1;
}
vector<string> ret;
for (auto x : h) {
if (x.second == 1) continue;
ret.push_back(x.first);
}
return ret;
}
};class Solution {
public:
// 判断单词包含重复字母
// 可以采用哈希
// 将字母映射为26维的向量
// 向量每一位为0或者1
// one-hot 编码
int maxProduct(vector<string>& words) {
vector<int> mark(words.size());
for (int i = 0; i < words.size(); ++i) {
for (auto c : words[i]) {
// 如果出现了 就将第i位的设成1
// 1 << (c - 'a')就是将1左移到它对应的mark字母位上
mark[i] |= (1 << (c - 'a'));
}
}
int ans = 0;
// 大暴力循环求max
for (int i = 0; i < words.size(); i++) {
for (int j = i + 1; j < words.size(); j++) {
// 说明有相同的位子
// 没有相同的应该是one-hot编码的每一位都不一样
// 按位& = 0
if (mark[i] & mark[j]) continue;
ans = max(ans, int(words[i].size() * words[j].size()));
}
}
return ans;
}
};在杨氏矩阵中,有两个特殊的点 一个是右上的点(15) 一个是左下的点(18) 如果
m[i][j]比右上的点大 说明他一定在下一行 因为第一行的最右边的是这一行最大的! 这样就能缩小查找范围 左下同理
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
// locate 到右上角的元素
int i = 0, j = matrix[0].size() - 1;
// 确定边界条件
// i从上往下走 j从右往左走
while (i < matrix.size() && j >= 0) {
if (matrix[i][j] == target) return true;
if (matrix[i][j] < target) i += 1;
else j -= 1;
}
return false;
}
};假设有5个节点,3枚硬币
那么跟节点就得把两个给子树
这样才能5个节点对5个硬币
也就是边e的流向是2 -> e产生了两次移动次数
可总结出:可以一次统计子树的节点数量和金币数量,差值就是流经边的数量,也就是移动次数
统计每个子树的节点数 硬币数 对差值求和
class Solution {
public:
// 硬币的流向一定是单向的
// 流过每条边
// 因为如果是双向的,那为什么不取单向的差值呢?
// n统计当前子树的节点数量
// m统计硬币数量
int getResult(TreeNode *root, int &n, int &m) {
n = m = 0;
if (root == nullptr) return 0;
n = 1, m = root->val;
int ans = 0, n1, m1;
// 左子树内部的所有的
ans += getResult(root->left, n1, m1);
// 在根节点看左子树(把左子树当成整体的)
ans += abs(n1 - m1);
n += n1, m += m1;
ans += getResult(root->right, n1, m1);
ans += abs(n1 - m1);
n += n1, m += m1;
return ans;
}
int distributeCoins(TreeNode* root) {
int n, m;
return getResult(root, n, m);
}
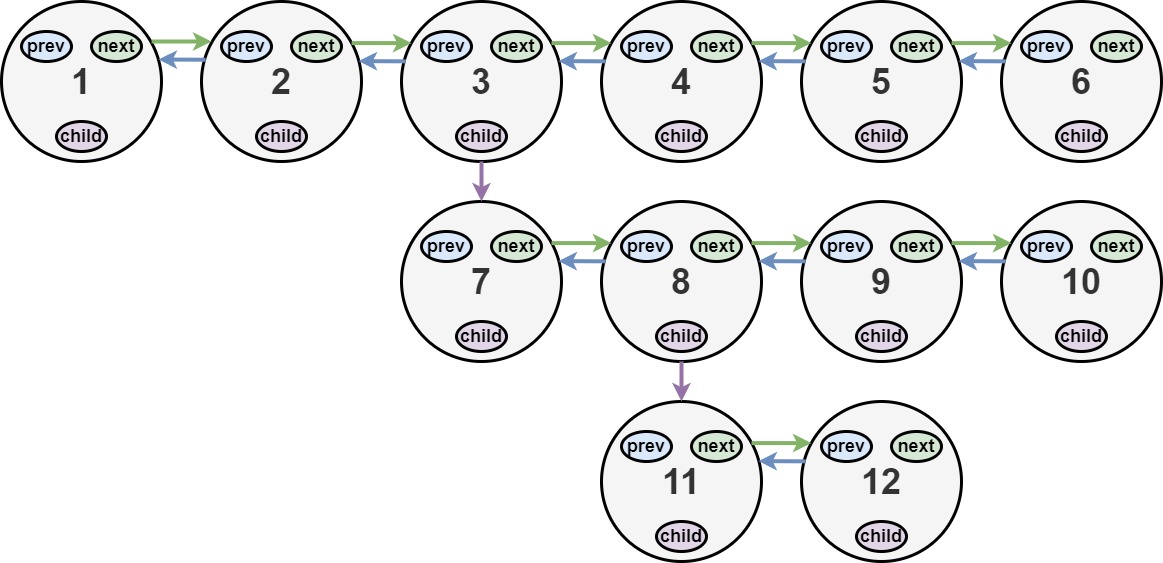
};我们可以将11,12插入8,9之间形成新的7,8,11,12,9,10子链表
然后再将新的子链表插入3, 4之间
因为问题具有完全包含关系,那就拆成子问题
所以可以用递归做
// 也是一个递归的过程
class Solution {
public:
Node* flatten(Node* head) {
Node *p = head, *k, *q;
while (p) {
if (p->child) {
// 对孩子扁平化
// 形成新的链表k
q = p->next;
k = flatten(p->child);
// 注意p的孩子就不要了 新的链表是p->next了
p->child = nullptr;
// 将p和k链接
// q = p->next;
// p->next = k;
p->next = k;
k->prev = p;
while (p->next) p = p->next;
// k->last->next = q;
p->next = q;
if (q) q->prev = p;
}
p = p->next;
}
return head;
}
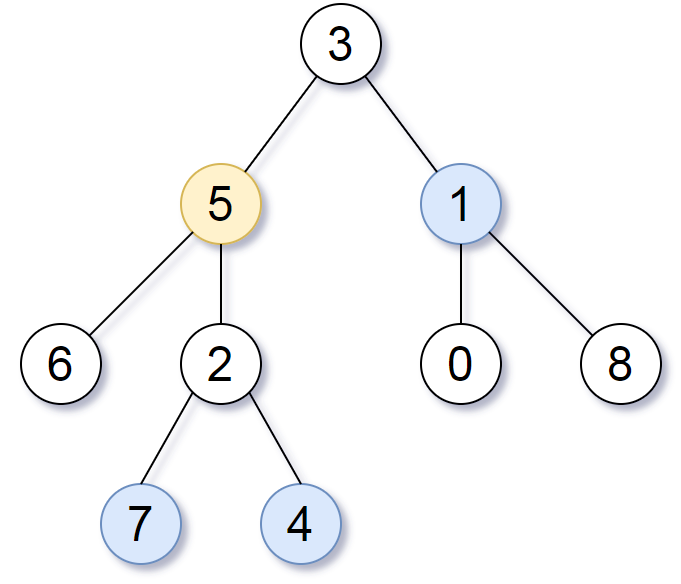
};也就是站在当前节点,向下看k层的。这个靠一个简单的dfs就可(层序遍历)
现在是在回溯的过程中
假设target深度为1,A为当前的root
target的子树已经递归完了
现在要去A的右子树找距离target为k的
那么不就是找离Ak - target距离A的距离的距离的点么!
再去右子树中,往下一层就变成了查找和A右孩子距离为k - 2的节点
再扩大一点 如果是D节点 那么就是在D的子树找深度为k - 3的
也就是每往上回溯一层,距离k是要➖1的
class Solution {
public:
// dfs 向下找距离为k的节点
void dfs(TreeNode *root, int c, int k, vector<int> &ret) {
if (k < 0) return ;
if (root == nullptr) return ;
if (c == k) {
ret.push_back(root->val);
return ;
}
dfs(root->left, c + 1, k, ret);
dfs(root->right, c + 1, k, ret);
return ;
}
TreeNode *getResult(TreeNode *root, TreeNode *target, int &k, vector<int> &ret) {
if (root == nullptr) return nullptr;
// 先考虑最简单的情况
// 向下查找距离为k的 就是深度为k的
// 层序遍历就行了
if (root == target) {
// dfs找第k层的节点
dfs(root, 0, k, ret);
return root;
}
// target在左子树
// 就得特殊处理右子树
if (getResult(root->left, target, k, ret)) {
k -= 1;
if (k == 0) ret.push_back(root->val);
dfs(root->right, 0, k - 1, ret);
return target;
// 在左子树中没找到target 那就去右子树试一下
} else if (getResult(root->right, target, k, ret)) {
k -= 1;
if (k == 0) ret.push_back(root->val);
dfs(root->left, 0, k - 1, ret);
return target;
}
return nullptr;
}
vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
vector<int> ret;
getResult(root, target, k, ret);
return ret;
}
};