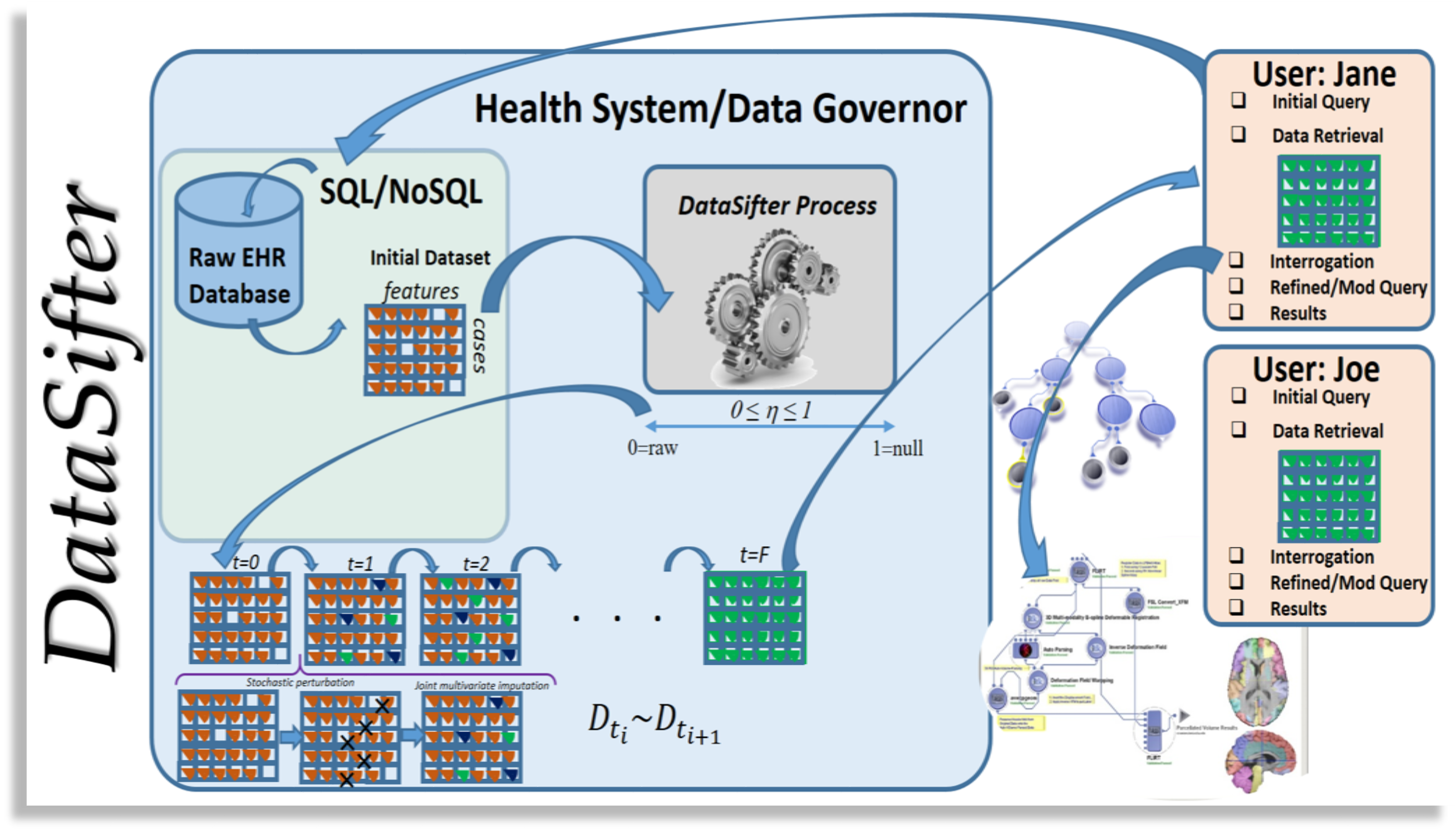
Statistical Obfuscation of Sensitive Time-varying Correlated Data
The DataSifter provides critical support for collaborative data sharing, open-science networking, and secure information exchange. In its core, the DataSifter implements a novel statistical obfuscation technique that optimizes privacy protection (for secure and safe information exchange) and utility (preservation of the information content and analytical value) of datasets. Simulation codes can be found in the Simulation Studies folder.
Nina Zhou, Lu Wang, Simeone Marino, Yi Zhao, Ivo Dinov and the SOCR Team.
Install both, the light-weight version DataSifter-Lite (V 1.0) and this new and expanded version DataSifter II.
library(devtools)
install_github("SOCR/DataSifterII")
install_github("SOCR/DataSifter")
library(DataSifterII)
library(DataSifter.lite)
Obfuscate time-varying and time-invariant data separately.
data(sim)
#DS II on Time-varying data
set.seed(1234)
siftsim <- repSifter(data=sim,mispct = 0.2,lnames=c("Y","K"),
timevar = "visit",ID="ID")
sifttv <- siftsim[[1]] %>% dplyr::select(c("ID","visit","Y","K"))
#DS I on Time-invariant data
sim_cs <- sim %>% filter(visit==1) %>% dplyr::select(-c("visit","Y","K"))
sifter_sim_cs <- dataSifter(level="medium",data = sim_cs,subjID = "ID",nomissing = TRUE)
#Merging two together
siftsim_final <- left_join(siftsim[[1]] %>% dplyr::select(c("ID","visit","Y","K")),
cbind(ID=as.factor(sim_cs$ID),sifter_sim_cs),by="ID")
The generating models for Y and K are
E(Y)=10+20*X1-15*X2-6*X3+0.8*visit,
and E(K)=15+12*Y+5*X4+10*X5+2*visit.
#Data Privacy
boxplot(pifv(sim,siftsim_final))
# define original coefficients for simulation model
orig_coeff <- c(10, 20, -15, -6, 0.8)
k_orig_coeff <- c(15, 12, 5, 10, 2)
#Data utility
library(nlme)
#Y=10+20*x1-15*x2-6*x3+0.8*visit+b+e
Ymodel <- lme(Y~x1+x2+x3+visit,random = ~1|ID,data=siftsim_final)
summary(Ymodel)
intervals(Ymodel)
#K=15+12*Y+5*x4+10*x5+2*visit+b1+e1
Kmodel <- lme(K~Y+x4+x5+visit,random = ~1|ID,data=siftsim_final)
summary(Kmodel)
intervals(Kmodel)
Compare the actual simulation-model coefficients and the estimated coefficients by fitting the model on the sifted data.
data.frame(cbind(Ymodel$coefficients$fixed, orig_coeff))
data.frame(cbind(Kmodel$coefficients$fixed, k_orig_coeff))
- DataSifter-Lite (V 1.0)
- DataSifter website
- Marino, S, Zhou, N, Zhao, Yi, Wang, L, Wu Q, and Dinov, ID. (2019) DataSifter: Statistical Obfuscation of Electronic Health Records and Other Sensitive Datasets, Journal of Statistical Computation and Simulation, 89(2): 249–271, DOI: 10.1080/00949655.2018.1545228.
- Zhou, N, Wang, L, Marino, S, Zhao, Y, Dinov, ID. (2022) DataSifter II: Partially Synthetic Data Sharing of Sensitive Information Containing Time-varying Correlated Observations, Journal of Algorithms & Computational Technology, Volume 15: 1–17, DOI: 10.1177/17483026211065379.