diff --git a/Project.toml b/Project.toml
index 3d89691c..0efa988f 100644
--- a/Project.toml
+++ b/Project.toml
@@ -1,7 +1,7 @@
name = "ReservoirComputing"
uuid = "7c2d2b1e-3dd4-11ea-355a-8f6a8116e294"
authors = ["Francesco Martinuzzi"]
-version = "0.9.4"
+version = "0.9.5"
[deps]
Adapt = "79e6a3ab-5dfb-504d-930d-738a2a938a0e"
diff --git a/README.md b/README.md
index 8a30afa8..9172725e 100644
--- a/README.md
+++ b/README.md
@@ -2,13 +2,13 @@
[](https://julialang.zulipchat.com/#narrow/stream/279055-sciml-bridged)
[](https://docs.sciml.ai/ReservoirComputing/stable/)
- [](https://arxiv.org/abs/2204.05117)
+[](https://arxiv.org/abs/2204.05117)
[](https://codecov.io/gh/SciML/ReservoirComputing.jl)
[](https://github.com/SciML/ReservoirComputing.jl/actions?query=workflow%3ACI)
[](https://buildkite.com/julialang/reservoircomputing-dot-jl)
-[](https://github.com/SciML/ColPrac)
+[](https://github.com/SciML/ColPrac)
[](https://github.com/SciML/SciMLStyle)

@@ -23,58 +23,68 @@ To illustrate the workflow of this library we will showcase how it is possible t
using ReservoirComputing, OrdinaryDiffEq
#lorenz system parameters
-u0 = [1.0,0.0,0.0]
-tspan = (0.0,200.0)
-p = [10.0,28.0,8/3]
+u0 = [1.0, 0.0, 0.0]
+tspan = (0.0, 200.0)
+p = [10.0, 28.0, 8 / 3]
#define lorenz system
-function lorenz(du,u,p,t)
- du[1] = p[1]*(u[2]-u[1])
- du[2] = u[1]*(p[2]-u[3]) - u[2]
- du[3] = u[1]*u[2] - p[3]*u[3]
+function lorenz(du, u, p, t)
+ du[1] = p[1] * (u[2] - u[1])
+ du[2] = u[1] * (p[2] - u[3]) - u[2]
+ du[3] = u[1] * u[2] - p[3] * u[3]
end
#solve and take data
-prob = ODEProblem(lorenz, u0, tspan, p)
-data = solve(prob, ABM54(), dt=0.02)
+prob = ODEProblem(lorenz, u0, tspan, p)
+data = solve(prob, ABM54(), dt = 0.02)
shift = 300
train_len = 5000
predict_len = 1250
#one step ahead for generative prediction
-input_data = data[:, shift:shift+train_len-1]
-target_data = data[:, shift+1:shift+train_len]
+input_data = data[:, shift:(shift + train_len - 1)]
+target_data = data[:, (shift + 1):(shift + train_len)]
-test = data[:,shift+train_len:shift+train_len+predict_len-1]
+test = data[:, (shift + train_len):(shift + train_len + predict_len - 1)]
```
+
Now that we have the data we can initialize the ESN with the chosen parameters. Given that this is a quick example we are going to change the least amount of possible parameters. For more detailed examples and explanations of the functions please refer to the documentation.
+
```julia
res_size = 300
-esn = ESN(input_data;
- reservoir = RandSparseReservoir(res_size, radius=1.2, sparsity=6/res_size),
- input_layer = WeightedLayer(),
- nla_type = NLAT2())
+esn = ESN(input_data;
+ reservoir = RandSparseReservoir(res_size, radius = 1.2, sparsity = 6 / res_size),
+ input_layer = WeightedLayer(),
+ nla_type = NLAT2())
```
The echo state network can now be trained and tested. If not specified, the training will always be Ordinary Least Squares regression. The full range of training methods is detailed in the documentation.
+
```julia
output_layer = train(esn, target_data)
output = esn(Generative(predict_len), output_layer)
```
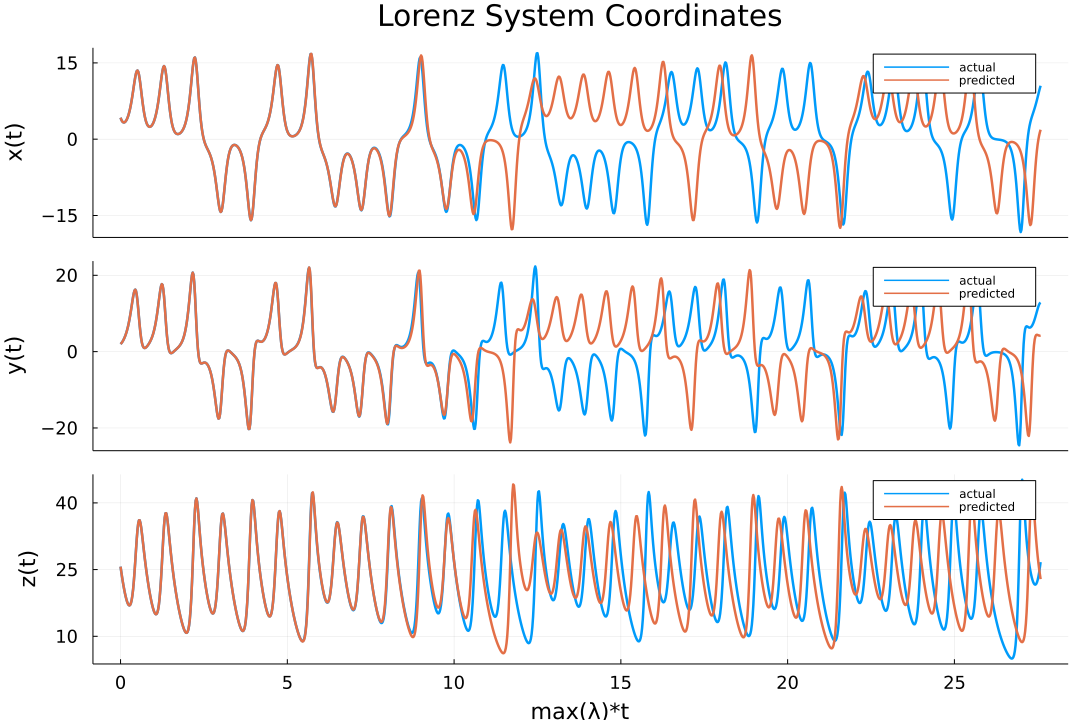
The data is returned as a matrix, `output` in the code above, that contains the predicted trajectories. The results can now be easily plotted (for the actual script used to obtain this plot please refer to the documentation):
+
```julia
using Plots
-plot(transpose(output),layout=(3,1), label="predicted")
-plot!(transpose(test),layout=(3,1), label="actual")
+plot(transpose(output), layout = (3, 1), label = "predicted")
+plot!(transpose(test), layout = (3, 1), label = "actual")
```
+
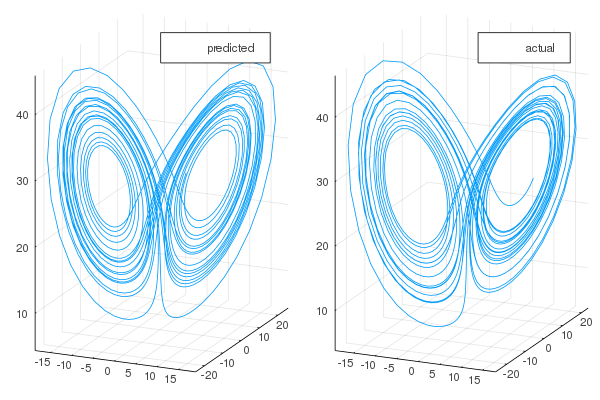
One can also visualize the phase space of the attractor and the comparison with the actual one:
+
```julia
-plot(transpose(output)[:,1], transpose(output)[:,2], transpose(output)[:,3], label="predicted")
-plot!(transpose(test)[:,1], transpose(test)[:,2], transpose(test)[:,3], label="actual")
+plot(transpose(output)[:, 1],
+ transpose(output)[:, 2],
+ transpose(output)[:, 3],
+ label = "predicted")
+plot!(transpose(test)[:, 1], transpose(test)[:, 2], transpose(test)[:, 3], label = "actual")
```
+
## Citing
diff --git a/docs/make.jl b/docs/make.jl
index 9fa9ec58..7d697952 100644
--- a/docs/make.jl
+++ b/docs/make.jl
@@ -8,13 +8,12 @@ ENV["GKSwstype"] = "100"
include("pages.jl")
makedocs(modules = [ReservoirComputing],
- sitename = "ReservoirComputing.jl",
- clean = true, doctest = false, linkcheck = true,
- warnonly = [:missing_docs],
- format = Documenter.HTML(
- assets = ["assets/favicon.ico"],
- canonical = "https://docs.sciml.ai/ReservoirComputing/stable/"),
- pages = pages)
+ sitename = "ReservoirComputing.jl",
+ clean = true, doctest = false, linkcheck = true,
+ warnonly = [:missing_docs],
+ format = Documenter.HTML(assets = ["assets/favicon.ico"],
+ canonical = "https://docs.sciml.ai/ReservoirComputing/stable/"),
+ pages = pages)
deploydocs(repo = "github.com/SciML/ReservoirComputing.jl.git";
- push_preview = true)
+ push_preview = true)
diff --git a/docs/pages.jl b/docs/pages.jl
index fb96f752..309f76fa 100644
--- a/docs/pages.jl
+++ b/docs/pages.jl
@@ -1,21 +1,21 @@
pages = [
"ReservoirComputing.jl" => "index.md",
"General Settings" => Any["Changing Training Algorithms" => "general/different_training.md",
- "Altering States" => "general/states_variation.md",
- "Generative vs Predictive" => "general/predictive_generative.md"],
+ "Altering States" => "general/states_variation.md",
+ "Generative vs Predictive" => "general/predictive_generative.md"],
"Echo State Network Tutorials" => Any["Lorenz System Forecasting" => "esn_tutorials/lorenz_basic.md",
- #"Mackey-Glass Forecasting on GPU" => "esn_tutorials/mackeyglass_basic.md",
- "Using Different Layers" => "esn_tutorials/change_layers.md",
- "Using Different Reservoir Drivers" => "esn_tutorials/different_drivers.md",
- #"Using Different Training Methods" => "esn_tutorials/different_training.md",
- "Deep Echo State Networks" => "esn_tutorials/deep_esn.md",
- "Hybrid Echo State Networks" => "esn_tutorials/hybrid.md"],
+ #"Mackey-Glass Forecasting on GPU" => "esn_tutorials/mackeyglass_basic.md",
+ "Using Different Layers" => "esn_tutorials/change_layers.md",
+ "Using Different Reservoir Drivers" => "esn_tutorials/different_drivers.md",
+ #"Using Different Training Methods" => "esn_tutorials/different_training.md",
+ "Deep Echo State Networks" => "esn_tutorials/deep_esn.md",
+ "Hybrid Echo State Networks" => "esn_tutorials/hybrid.md"],
"Reservoir Computing with Cellular Automata" => "reca_tutorials/reca.md",
"API Documentation" => Any["Training Algorithms" => "api/training.md",
- "States Modifications" => "api/states.md",
- "Prediction Types" => "api/predict.md",
- "Echo State Networks" => "api/esn.md",
- "ESN Layers" => "api/esn_layers.md",
- "ESN Drivers" => "api/esn_drivers.md",
- "ReCA" => "api/reca.md"],
+ "States Modifications" => "api/states.md",
+ "Prediction Types" => "api/predict.md",
+ "Echo State Networks" => "api/esn.md",
+ "ESN Layers" => "api/esn_layers.md",
+ "ESN Drivers" => "api/esn_drivers.md",
+ "ReCA" => "api/reca.md"],
]
diff --git a/docs/src/api/esn.md b/docs/src/api/esn.md
index ff03dc8c..1caacdd1 100644
--- a/docs/src/api/esn.md
+++ b/docs/src/api/esn.md
@@ -1,16 +1,28 @@
# Echo State Networks
+
+The core component of an ESN is the `ESN` type. It represents the entire Echo State Network and includes parameters for configuring the reservoir, input scaling, and output weights. Here's the documentation for the `ESN` type:
+
```@docs
ESN
```
-In addition to all the components that can be explored in the documentation, a couple components need a separate introduction. The ```variation``` arguments can be
+## Variations
+
+In addition to the standard `ESN` model, there are variations that allow for deeper customization of the underlying model. Currently, there are two available variations: `Default` and `Hybrid`. These variations provide different ways to configure the ESN. Here's the documentation for the variations:
+
```@docs
Default
Hybrid
```
-These arguments detail a deeper variation of the underlying model, and they need a separate call. For the moment, the most complex is the ```Hybrid``` call, but this can and will change in the future.
-All ESN models can be trained using the following call:
+The `Hybrid` variation is the most complex option and offers additional customization. Note that more variations may be added in the future to provide even greater flexibility.
+
+## Training
+
+To train an ESN model, you can use the `train` function. It takes the ESN model, training data, and other optional parameters as input and returns a trained model. Here's the documentation for the train function:
+
```@docs
train
```
+
+With these components and variations, you can configure and train ESN models for various time series and sequential data prediction tasks.
diff --git a/docs/src/api/esn_drivers.md b/docs/src/api/esn_drivers.md
index a11ec35b..0bf0a388 100644
--- a/docs/src/api/esn_drivers.md
+++ b/docs/src/api/esn_drivers.md
@@ -1,13 +1,16 @@
# ESN Drivers
+
```@docs
RNN
MRNN
GRU
```
-The ```GRU``` driver also provides the user with the choice of the possible variants:
+
+The `GRU` driver also provides the user with the choice of the possible variants:
+
```@docs
FullyGated
Minimal
```
-Please refer to the original papers for more detail about these architectures.
+Please refer to the original papers for more detail about these architectures.
diff --git a/docs/src/api/esn_layers.md b/docs/src/api/esn_layers.md
index 76be5268..bb3b53de 100644
--- a/docs/src/api/esn_layers.md
+++ b/docs/src/api/esn_layers.md
@@ -1,6 +1,7 @@
# ESN Layers
## Input Layers
+
```@docs
WeightedLayer
DenseLayer
@@ -9,16 +10,22 @@
MinimumLayer
NullLayer
```
-The signs in the ```MinimumLayer``` are chosen based on the following methods:
+
+The signs in the `MinimumLayer` are chosen based on the following methods:
+
```@docs
BernoulliSample
IrrationalSample
```
+
To derive the matrix one can call the following function:
+
```@docs
create_layer
```
-To create new input layers, it suffices to define a new struct containing the needed parameters of the new input layer. This struct will need to be an ```AbstractLayer```, so the ```create_layer``` function can be dispatched over it. The workflow should follow this snippet:
+
+To create new input layers, it suffices to define a new struct containing the needed parameters of the new input layer. This struct will need to be an `AbstractLayer`, so the `create_layer` function can be dispatched over it. The workflow should follow this snippet:
+
```julia
#creation of the new struct for the layer
struct MyNewLayer <: AbstractLayer
@@ -32,6 +39,7 @@ end
```
## Reservoirs
+
```@docs
RandSparseReservoir
PseudoSVDReservoir
@@ -43,11 +51,13 @@ end
```
Like for the input layers, to actually build the matrix of the reservoir, one can call the following function:
+
```@docs
create_reservoir
```
-To create a new reservoir, the procedure is similar to the one for the input layers. First, the definition of the new struct of type ```AbstractReservoir``` with the reservoir parameters is needed. Then the dispatch over the ```create_reservoir``` function makes the model actually build the reservoir matrix. An example of the workflow is given in the following snippet:
+To create a new reservoir, the procedure is similar to the one for the input layers. First, the definition of the new struct of type `AbstractReservoir` with the reservoir parameters is needed. Then the dispatch over the `create_reservoir` function makes the model actually build the reservoir matrix. An example of the workflow is given in the following snippet:
+
```julia
#creation of the new struct for the reservoir
struct MyNewReservoir <: AbstractReservoir
diff --git a/docs/src/api/predict.md b/docs/src/api/predict.md
index cf3699a4..5409d78e 100644
--- a/docs/src/api/predict.md
+++ b/docs/src/api/predict.md
@@ -1,4 +1,5 @@
# Prediction Types
+
```@docs
Generative
Predictive
diff --git a/docs/src/api/reca.md b/docs/src/api/reca.md
index dcbc86df..48f134dd 100644
--- a/docs/src/api/reca.md
+++ b/docs/src/api/reca.md
@@ -1,11 +1,13 @@
# Reservoir Computing with Cellular Automata
+
```@docs
RECA
```
The input encodings are the equivalent of the input matrices of the ESNs. These are the available encodings:
+
```@docs
RandomMapping
```
-The training and prediction follow the same workflow as the ESN. It is important to note that currently we were unable to find any papers using these models with a ```Generative``` approach for the prediction, so full support is given only to the ```Predictive``` method.
+The training and prediction follow the same workflow as the ESN. It is important to note that currently we were unable to find any papers using these models with a `Generative` approach for the prediction, so full support is given only to the `Predictive` method.
diff --git a/docs/src/api/states.md b/docs/src/api/states.md
index 282863e8..5a4e5686 100644
--- a/docs/src/api/states.md
+++ b/docs/src/api/states.md
@@ -1,6 +1,7 @@
# States Modifications
## Padding and Estension
+
```@docs
StandardStates
ExtendedStates
@@ -9,6 +10,7 @@
```
## Non Linear Transformations
+
```@docs
NLADefault
NLAT1
diff --git a/docs/src/api/training.md b/docs/src/api/training.md
index b34f046b..a11b2034 100644
--- a/docs/src/api/training.md
+++ b/docs/src/api/training.md
@@ -1,13 +1,16 @@
# Training Algorithms
## Linear Models
+
```@docs
StandardRidge
LinearModel
```
## Gaussian Regression
+
Currently, v0.9 is unavailable.
## Support Vector Regression
-Support Vector Regression is possible using a direct call to [LIBSVM](https://github.com/JuliaML/LIBSVM.jl) regression methods. Instead of a wrapper, please refer to the use of ```LIBSVM.AbstractSVR``` in the original library.
+
+Support Vector Regression is possible using a direct call to [LIBSVM](https://github.com/JuliaML/LIBSVM.jl) regression methods. Instead of a wrapper, please refer to the use of `LIBSVM.AbstractSVR` in the original library.
diff --git a/docs/src/esn_tutorials/change_layers.md b/docs/src/esn_tutorials/change_layers.md
index 0a659cd5..5cfb65cf 100644
--- a/docs/src/esn_tutorials/change_layers.md
+++ b/docs/src/esn_tutorials/change_layers.md
@@ -1,13 +1,16 @@
# Using Different Layers
+
A great deal of effort in the ESNs field is devoted to finding the ideal construction for the reservoir matrices. With a simple interface using ReservoirComputing.jl it is possible to leverage the currently implemented matrix construction methods for both the reservoir and the input layer. On this page, it is showcased how it is possible to change both of these layers.
The `input_init` keyword argument provided with the `ESN` constructor allows for changing the input layer. The layers provided in ReservoirComputing.jl are the following:
-- ```WeightedLayer(scaling)```
-- ```DenseLayer(scaling)```
-- ```SparseLayer(scaling, sparsity)```
-- ```MinimumLayer(weight, sampling)```
-- ```InformedLayer(model_in_size; scaling=0.1, gamma=0.5)```
-In addition, the user can define a custom layer following this workflow:
+
+ - `WeightedLayer(scaling)`
+ - `DenseLayer(scaling)`
+ - `SparseLayer(scaling, sparsity)`
+ - `MinimumLayer(weight, sampling)`
+ - `InformedLayer(model_in_size; scaling=0.1, gamma=0.5)`
+ In addition, the user can define a custom layer following this workflow:
+
```julia
#creation of the new struct for the layer
struct MyNewLayer <: AbstractLayer
@@ -19,14 +22,17 @@ function create_layer(input_layer::MyNewLayer, res_size, in_size)
#the new algorithm to build the input layer goes here
end
```
+
Similarly the `reservoir_init` keyword argument provides the possibility to change the construction for the reservoir matrix. The available reservoir are:
-- ```RandSparseReservoir(res_size, radius, sparsity)```
-- ```PseudoSVDReservoir(res_size, max_value, sparsity, sorted, reverse_sort)```
-- ```DelayLineReservoir(res_size, weight)```
-- ```DelayLineBackwardReservoir(res_size, weight, fb_weight)```
-- ```SimpleCycleReservoir(res_size, weight)```
-- ```CycleJumpsReservoir(res_size, cycle_weight, jump_weight, jump_size)```
-And, like before, it is possible to build a custom reservoir by following this workflow:
+
+ - `RandSparseReservoir(res_size, radius, sparsity)`
+ - `PseudoSVDReservoir(res_size, max_value, sparsity, sorted, reverse_sort)`
+ - `DelayLineReservoir(res_size, weight)`
+ - `DelayLineBackwardReservoir(res_size, weight, fb_weight)`
+ - `SimpleCycleReservoir(res_size, weight)`
+ - `CycleJumpsReservoir(res_size, cycle_weight, jump_weight, jump_size)`
+ And, like before, it is possible to build a custom reservoir by following this workflow:
+
```julia
#creation of the new struct for the reservoir
struct MyNewReservoir <: AbstractReservoir
@@ -40,9 +46,11 @@ end
```
## Example of a minimally complex ESN
+
Using [^1] and [^2] as references, this section will provide an example of how to change both the input layer and the reservoir for ESNs. The full script for this example can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_layers/layers.jl). This example was run on Julia v1.7.2.
The task for this example will be the one step ahead prediction of the Henon map. To obtain the data, one can leverage the package [DynamicalSystems.jl](https://juliadynamics.github.io/DynamicalSystems.jl/dev/). The data is scaled to be between -1 and 1.
+
```@example mesn
using PredefinedDynamicalSystems
train_len = 3000
@@ -51,13 +59,13 @@ predict_len = 2000
ds = PredefinedDynamicalSystems.henon()
traj, time = trajectory(ds, 7000)
data = Matrix(traj)'
-data = (data .-0.5) .* 2
+data = (data .- 0.5) .* 2
shift = 200
-training_input = data[:, shift:shift+train_len-1]
-training_target = data[:, shift+1:shift+train_len]
-testing_input = data[:,shift+train_len:shift+train_len+predict_len-1]
-testing_target = data[:,shift+train_len+1:shift+train_len+predict_len]
+training_input = data[:, shift:(shift + train_len - 1)]
+training_target = data[:, (shift + 1):(shift + train_len)]
+testing_input = data[:, (shift + train_len):(shift + train_len + predict_len - 1)]
+testing_target = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
Now it is possible to define the input layers and reservoirs we want to compare and run the comparison in a simple for loop. The accuracy will be tested using the mean squared deviation `msd` from [StatsBase](https://juliastats.org/StatsBase.jl/stable/).
@@ -66,11 +74,14 @@ Now it is possible to define the input layers and reservoirs we want to compare
using ReservoirComputing, StatsBase
res_size = 300
-input_layer = [MinimumLayer(0.85, IrrationalSample()), MinimumLayer(0.95, IrrationalSample())]
-reservoirs = [SimpleCycleReservoir(res_size, 0.7),
- CycleJumpsReservoir(res_size, cycle_weight=0.7, jump_weight=0.2, jump_size=5)]
+input_layer = [
+ MinimumLayer(0.85, IrrationalSample()),
+ MinimumLayer(0.95, IrrationalSample()),
+]
+reservoirs = [SimpleCycleReservoir(res_size, 0.7),
+ CycleJumpsReservoir(res_size, cycle_weight = 0.7, jump_weight = 0.2, jump_size = 5)]
-for i=1:length(reservoirs)
+for i in 1:length(reservoirs)
esn = ESN(training_input;
input_layer = input_layer[i],
reservoir = reservoirs[i])
@@ -79,11 +90,10 @@ for i=1:length(reservoirs)
println(msd(testing_target, output))
end
```
-As it is possible to see, changing layers in ESN models is straightforward. Be sure to check the API documentation for a full list of reservoirs and layers.
+As it is possible to see, changing layers in ESN models is straightforward. Be sure to check the API documentation for a full list of reservoirs and layers.
## Bibliography
-[^1]: Rodan, Ali, and Peter Tiňo. “Simple deterministically constructed cycle reservoirs with regular jumps.” Neural computation 24.7 (2012): 1822-1852.
+[^1]: Rodan, Ali, and Peter Tiňo. “Simple deterministically constructed cycle reservoirs with regular jumps.” Neural computation 24.7 (2012): 1822-1852.
[^2]: Rodan, Ali, and Peter Tiňo. “Minimum complexity echo state network.” IEEE transactions on neural networks 22.1 (2010): 131-144.
-
diff --git a/docs/src/esn_tutorials/deep_esn.md b/docs/src/esn_tutorials/deep_esn.md
index 6619f722..bd4f7b46 100644
--- a/docs/src/esn_tutorials/deep_esn.md
+++ b/docs/src/esn_tutorials/deep_esn.md
@@ -1,24 +1,26 @@
# Deep Echo State Networks
-Deep Echo State Network architectures started to gain some traction recently. In this guide, we illustrate how it is possible to use ReservoirComputing.jl to build a deep ESN.
+Deep Echo State Network architectures started to gain some traction recently. In this guide, we illustrate how it is possible to use ReservoirComputing.jl to build a deep ESN.
The network implemented in this library is taken from [^1]. It works by stacking reservoirs on top of each other, feeding the output from one into the next. The states are obtained by merging all the inner states of the stacked reservoirs. For a more in-depth explanation, refer to the paper linked above. The full script for this example can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/deep-esn/deepesn.jl). This example was run on Julia v1.7.2.
## Lorenz Example
+
For this example, we are going to reuse the Lorenz data used in the [Lorenz System Forecasting](@ref) example.
+
```@example deep_lorenz
using OrdinaryDiffEq
#define lorenz system
-function lorenz!(du,u,p,t)
- du[1] = 10.0*(u[2]-u[1])
- du[2] = u[1]*(28.0-u[3]) - u[2]
- du[3] = u[1]*u[2] - (8/3)*u[3]
+function lorenz!(du, u, p, t)
+ du[1] = 10.0 * (u[2] - u[1])
+ du[2] = u[1] * (28.0 - u[3]) - u[2]
+ du[3] = u[1] * u[2] - (8 / 3) * u[3]
end
#solve and take data
-prob = ODEProblem(lorenz!, [1.0,0.0,0.0], (0.0,200.0))
-data = solve(prob, ABM54(), dt=0.02)
+prob = ODEProblem(lorenz!, [1.0, 0.0, 0.0], (0.0, 200.0))
+data = solve(prob, ABM54(), dt = 0.02)
#determine shift length, training length and prediction length
shift = 300
@@ -26,22 +28,23 @@ train_len = 5000
predict_len = 1250
#split the data accordingly
-input_data = data[:, shift:shift+train_len-1]
-target_data = data[:, shift+1:shift+train_len]
-test_data = data[:,shift+train_len+1:shift+train_len+predict_len]
+input_data = data[:, shift:(shift + train_len - 1)]
+target_data = data[:, (shift + 1):(shift + train_len)]
+test_data = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
-Again, it is *important* to notice that the data needs to be formatted in a matrix, with the features as rows and time steps as columns, as in this example. This is needed even if the time series consists of single values.
+Again, it is *important* to notice that the data needs to be formatted in a matrix, with the features as rows and time steps as columns, as in this example. This is needed even if the time series consists of single values.
+
+The construction of the ESN is also really similar. The only difference is that the reservoir can be fed as an array of reservoirs.
-The construction of the ESN is also really similar. The only difference is that the reservoir can be fed as an array of reservoirs.
```@example deep_lorenz
using ReservoirComputing
-reservoirs = [RandSparseReservoir(99, radius=1.1, sparsity=0.1),
- RandSparseReservoir(100, radius=1.2, sparsity=0.1),
- RandSparseReservoir(200, radius=1.4, sparsity=0.1)]
+reservoirs = [RandSparseReservoir(99, radius = 1.1, sparsity = 0.1),
+ RandSparseReservoir(100, radius = 1.2, sparsity = 0.1),
+ RandSparseReservoir(200, radius = 1.4, sparsity = 0.1)]
-esn = ESN(input_data;
+esn = ESN(input_data;
variation = Default(),
reservoir = reservoirs,
input_layer = DenseLayer(),
@@ -55,35 +58,39 @@ As it is possible to see, different sizes can be chosen for the different reserv
In addition to using the provided functions for the construction of the layers, the user can also choose to build their own matrix, or array of matrices, and feed that into the `ESN` in the same way.
The training and prediction follow the usual framework:
+
```@example deep_lorenz
-training_method = StandardRidge(0.0)
+training_method = StandardRidge(0.0)
output_layer = train(esn, target_data, training_method)
output = esn(Generative(predict_len), output_layer)
```
+
Plotting the results:
+
```@example deep_lorenz
using Plots
ts = 0.0:0.02:200.0
lorenz_maxlyap = 0.9056
-predict_ts = ts[shift+train_len+1:shift+train_len+predict_len]
-lyap_time = (predict_ts .- predict_ts[1])*(1/lorenz_maxlyap)
-
-p1 = plot(lyap_time, [test_data[1,:] output[1,:]], label = ["actual" "predicted"],
- ylabel = "x(t)", linewidth=2.5, xticks=false, yticks = -15:15:15);
-p2 = plot(lyap_time, [test_data[2,:] output[2,:]], label = ["actual" "predicted"],
- ylabel = "y(t)", linewidth=2.5, xticks=false, yticks = -20:20:20);
-p3 = plot(lyap_time, [test_data[3,:] output[3,:]], label = ["actual" "predicted"],
- ylabel = "z(t)", linewidth=2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
-
-
-plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
- layout=(3,1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize=15, yguidefontsize=15,
- legendfontsize=12, titlefontsize=20)
+predict_ts = ts[(shift + train_len + 1):(shift + train_len + predict_len)]
+lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
+
+p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
+ ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
+p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
+ ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
+p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
+ ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
+
+plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
+ layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
+ yguidefontsize = 15,
+ legendfontsize = 12, titlefontsize = 20)
```
Note that there is a known bug at the moment with using `WeightedLayer` as the input layer with the deep ESN. We are in the process of investigating and solving it. The leak coefficient for the reservoirs has to always be the same in the current implementation. This is also something we are actively looking into expanding.
## Documentation
+
[^1]: Gallicchio, Claudio, and Alessio Micheli. "_Deep echo state network (deepesn): A brief survey._" arXiv preprint arXiv:1712.04323 (2017).
diff --git a/docs/src/esn_tutorials/different_drivers.md b/docs/src/esn_tutorials/different_drivers.md
index 9b9fcd55..0a669451 100644
--- a/docs/src/esn_tutorials/different_drivers.md
+++ b/docs/src/esn_tutorials/different_drivers.md
@@ -1,41 +1,51 @@
# Using Different Reservoir Drivers
+
While the original implementation of the Echo State Network implemented the model using the equations of Recurrent Neural Networks to obtain non-linearity in the reservoir, other variations have been proposed in recent years. More specifically, the different drivers implemented in ReservoirComputing.jl are the multiple activation function RNN `MRNN()` and the Gated Recurrent Unit `GRU()`. To change them, it suffices to give the chosen method to the `ESN` keyword argument `reservoir_driver`. In this section, some examples, of their usage will be given, as well as a brief introduction to their equations.
## Multiple Activation Function RNN
+
Based on the double activation function ESN (DAFESN) proposed in [^1], the Multiple Activation Function ESN expands the idea and allows a custom number of activation functions to be used in the reservoir dynamics. This can be thought of as a linear combination of multiple activation functions with corresponding parameters.
+
```math
\mathbf{x}(t+1) = (1-\alpha)\mathbf{x}(t) + \lambda_1 f_1(\mathbf{W}\mathbf{x}(t)+\mathbf{W}_{in}\mathbf{u}(t)) + \dots + \lambda_D f_D(\mathbf{W}\mathbf{x}(t)+\mathbf{W}_{in}\mathbf{u}(t))
```
+
where ``D`` is the number of activation functions and respective parameters chosen.
-The method to call to use the multiple activation function ESN is `MRNN(activation_function, leaky_coefficient, scaling_factor)`. The arguments can be used as both `args` and `kwargs`. `activation_function` and `scaling_factor` have to be vectors (or tuples) containing the chosen activation functions and respective scaling factors (``f_1,...,f_D`` and ``\lambda_1,...,\lambda_D`` following the nomenclature introduced above). The `leaky_coefficient` represents ``\alpha`` and it is a single value.
+The method to call to use the multiple activation function ESN is `MRNN(activation_function, leaky_coefficient, scaling_factor)`. The arguments can be used as both `args` and `kwargs`. `activation_function` and `scaling_factor` have to be vectors (or tuples) containing the chosen activation functions and respective scaling factors (``f_1,...,f_D`` and ``\lambda_1,...,\lambda_D`` following the nomenclature introduced above). The `leaky_coefficient` represents ``\alpha`` and it is a single value.
Starting with the example, the data used is based on the following function based on the DAFESN paper [^1]. A full script of the example is available [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_drivers/mrnn/mrnn.jl). This example was run on Julia v1.7.2.
+
```@example mrnn
-u(t) = sin(t)+sin(0.51*t)+sin(0.22*t)+sin(0.1002*t)+sin(0.05343*t)
+u(t) = sin(t) + sin(0.51 * t) + sin(0.22 * t) + sin(0.1002 * t) + sin(0.05343 * t)
```
For this example, the type of prediction will be one step ahead. The metric used to assure a good prediction will be the normalized root-mean-square deviation `rmsd` from [StatsBase](https://juliastats.org/StatsBase.jl/stable/). Like in the other examples, first it is needed to gather the data:
+
```@example mrnn
train_len = 3000
predict_len = 2000
shift = 1
data = u.(collect(0.0:0.01:500))
-training_input = reduce(hcat, data[shift:shift+train_len-1])
-training_target = reduce(hcat, data[shift+1:shift+train_len])
-testing_input = reduce(hcat, data[shift+train_len:shift+train_len+predict_len-1])
-testing_target = reduce(hcat, data[shift+train_len+1:shift+train_len+predict_len])
+training_input = reduce(hcat, data[shift:(shift + train_len - 1)])
+training_target = reduce(hcat, data[(shift + 1):(shift + train_len)])
+testing_input = reduce(hcat,
+ data[(shift + train_len):(shift + train_len + predict_len - 1)])
+testing_target = reduce(hcat,
+ data[(shift + train_len + 1):(shift + train_len + predict_len)])
```
To follow the paper more closely, it is necessary to define a couple of activation functions. The numbering of them follows the ones in the paper. Of course, one can also use any custom-defined function, available in the base language or any activation function from [NNlib](https://fluxml.ai/Flux.jl/stable/models/nnlib/#Activation-Functions).
+
```@example mrnn
-f2(x) = (1-exp(-x))/(2*(1+exp(-x)))
-f3(x) = (2/pi)*atan((pi/2)*x)
-f4(x) = x/sqrt(1+x*x)
+f2(x) = (1 - exp(-x)) / (2 * (1 + exp(-x)))
+f3(x) = (2 / pi) * atan((pi / 2) * x)
+f4(x) = x / sqrt(1 + x * x)
```
It is now possible to build different drivers, using the parameters suggested by the paper. Also, in this instance, the numbering follows the test cases of the paper. In the end, a simple for loop is implemented to compare the different drivers and activation functions.
+
```@example mrnn
using ReservoirComputing, Random, StatsBase
@@ -47,14 +57,14 @@ base_case = RNN(tanh, 0.85)
#MRNN() test cases
#Parameter given as kwargs
-case3 = MRNN(activation_function=[tanh, f2],
- leaky_coefficient=0.85,
- scaling_factor=[0.5, 0.3])
+case3 = MRNN(activation_function = [tanh, f2],
+ leaky_coefficient = 0.85,
+ scaling_factor = [0.5, 0.3])
#Parameter given as kwargs
-case4 = MRNN(activation_function=[tanh, f3],
- leaky_coefficient=0.9,
- scaling_factor=[0.45, 0.35])
+case4 = MRNN(activation_function = [tanh, f3],
+ leaky_coefficient = 0.9,
+ scaling_factor = [0.45, 0.35])
#Parameter given as args
case5 = MRNN([tanh, f4], 0.9, [0.43, 0.13])
@@ -63,23 +73,26 @@ case5 = MRNN([tanh, f4], 0.9, [0.43, 0.13])
test_cases = [base_case, case3, case4, case5]
for case in test_cases
esn = ESN(training_input,
- input_layer = WeightedLayer(scaling=0.3),
- reservoir = RandSparseReservoir(100, radius=0.4),
+ input_layer = WeightedLayer(scaling = 0.3),
+ reservoir = RandSparseReservoir(100, radius = 0.4),
reservoir_driver = case,
states_type = ExtendedStates())
wout = train(esn, training_target, StandardRidge(10e-6))
output = esn(Predictive(testing_input), wout)
- println(rmsd(testing_target, output, normalize=true))
+ println(rmsd(testing_target, output, normalize = true))
end
```
In this example, it is also possible to observe the input of parameters to the methods `RNN()` `MRNN()`, both by argument and by keyword argument.
## Gated Recurrent Unit
+
Gated Recurrent Units (GRUs) [^2] have been proposed in more recent years with the intent of limiting notable problems of RNNs, like the vanishing gradient. This change in the underlying equations can be easily transported into the Reservoir Computing paradigm, by switching the RNN equations in the reservoir with the GRU equations. This approach has been explored in [^3] and [^4]. Different variations of GRU have been proposed [^5][^6]; this section is subdivided into different sections that go into detail about the governing equations and the implementation of them into ReservoirComputing.jl. Like before, to access the GRU reservoir driver, it suffices to change the `reservoir_diver` keyword argument for `ESN` with `GRU()`. All the variations that will be presented can be used in this package by leveraging the keyword argument `variant` in the method `GRU()` and specifying the chosen variant: `FullyGated()` or `Minimal()`. Other variations are possible by modifying the inner layers and reservoirs. The default is set to the standard version `FullyGated()`. The first section will go into more detail about the default of the `GRU()` method, and the following ones will refer to it to minimize repetitions. This example was run on Julia v1.7.2.
### Standard GRU
+
The equations for the standard GRU are as follows:
+
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r_{\text{in}}\mathbf{u}(t)+\mathbf{W}^r\mathbf{x}(t-1)+\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z_{\text{in}}\mathbf{u}(t)+\mathbf{W}^z\mathbf{x}(t-1)+\mathbf{b}_z) \\
@@ -87,19 +100,22 @@ The equations for the standard GRU are as follows:
\mathbf{x}(t) = \mathbf{z}(t) \odot \mathbf{x}(t-1)+(1-\mathbf{z}(t)) \odot \tilde{\mathbf{x}}(t)
```
-Going over the `GRU` keyword argument, it will be explained how to feed the desired input to the model.
- - `activation_function` is a vector with default values `[NNlib.sigmoid, NNlib.sigmoid, tanh]`. This argument controls the activation functions of the GRU, going from top to bottom. Changing the first element corresponds to changing the activation function for ``\mathbf{r}(t)`` and so on.
- - `inner_layer` is a vector with default values `fill(DenseLayer(), 2)`. This keyword argument controls the ``\mathbf{W}_{\text{in}}``s going from top to bottom like before.
- - `reservoir` is a vector with default value `fill(RandSparseReservoir(), 2)`. In a similar fashion to `inner_layer`, this keyword argument controls the reservoir matrix construction in a top to bottom order.
- - `bias` is again a vector with default value `fill(DenseLayer(), 2)`. It is meant to control the ``\mathbf{b}``s, going as usual from top to bottom.
- - `variant` controls the GRU variant. The default value is set to `FullyGated()`.
-
-It is important to notice that `inner_layer` and `reservoir` control every layer except ``\mathbf{W}_{in}`` and ``\mathbf{W}`` and ``\mathbf{b}``. These arguments are given as input to the `ESN()` call as `input_layer`, `reservoir` and `bias`.
+Going over the `GRU` keyword argument, it will be explained how to feed the desired input to the model.
+
+ - `activation_function` is a vector with default values `[NNlib.sigmoid, NNlib.sigmoid, tanh]`. This argument controls the activation functions of the GRU, going from top to bottom. Changing the first element corresponds to changing the activation function for ``\mathbf{r}(t)`` and so on.
+ - `inner_layer` is a vector with default values `fill(DenseLayer(), 2)`. This keyword argument controls the ``\mathbf{W}_{\text{in}}``s going from top to bottom like before.
+ - `reservoir` is a vector with default value `fill(RandSparseReservoir(), 2)`. In a similar fashion to `inner_layer`, this keyword argument controls the reservoir matrix construction in a top to bottom order.
+ - `bias` is again a vector with default value `fill(DenseLayer(), 2)`. It is meant to control the ``\mathbf{b}``s, going as usual from top to bottom.
+ - `variant` controls the GRU variant. The default value is set to `FullyGated()`.
+
+It is important to notice that `inner_layer` and `reservoir` control every layer except ``\mathbf{W}_{in}`` and ``\mathbf{W}`` and ``\mathbf{b}``. These arguments are given as input to the `ESN()` call as `input_layer`, `reservoir` and `bias`.
The following sections are going to illustrate the variations of the GRU architecture and how to obtain them in ReservoirComputing.jl
### Type 1
+
The first variation of the GRU is dependent only on the previous hidden state and the bias:
+
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r\mathbf{x}(t-1)+\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z\mathbf{x}(t-1)+\mathbf{b}_z) \\
@@ -108,7 +124,9 @@ The first variation of the GRU is dependent only on the previous hidden state an
To obtain this variation, it will suffice to set `inner_layer = fill(NullLayer(), 2)` and leaving the `variant = FullyGated()`.
### Type 2
+
The second variation only depends on the previous hidden state:
+
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r\mathbf{x}(t-1)) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z\mathbf{x}(t-1)) \\
@@ -117,7 +135,9 @@ The second variation only depends on the previous hidden state:
Similarly to before, to obtain this variation, it is only required to set `inner_layer = fill(NullLayer(), 2)` and `bias = fill(NullLayer(), 2)` while keeping `variant = FullyGated()`.
### Type 3
+
The final variation, before the minimal one, depends only on the biases
+
```math
\mathbf{r}(t) = \sigma (\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{b}_z) \\
@@ -125,8 +145,10 @@ The final variation, before the minimal one, depends only on the biases
This means that it is only needed to set `inner_layer = fill(NullLayer(), 2)` and `reservoir = fill(NullReservoir(), 2)` while keeping `variant = FullyGated()`.
-### Minimal
+### Minimal
+
The minimal GRU variation merges two gates into one:
+
```math
\mathbf{f}(t) = \sigma (\mathbf{W}^f_{\text{in}}\mathbf{u}(t)+\mathbf{W}^f\mathbf{x}(t-1)+\mathbf{b}_f) \\
\tilde{\mathbf{x}}(t) = \text{tanh}(\mathbf{W}_{in}\mathbf{u}(t)+\mathbf{W}(\mathbf{f}(t) \odot \mathbf{x}(t-1))+\mathbf{b}) \\
@@ -136,9 +158,11 @@ The minimal GRU variation merges two gates into one:
This variation can be obtained by setting `variation=Minimal()`. The `inner_layer`, `reservoir` and `bias` kwargs this time are **not** vectors, but must be defined like, for example `inner_layer = DenseLayer()` or `reservoir = SparseDenseReservoir()`.
### Examples
-To showcase the use of the `GRU()` method, this section will only illustrate the standard `FullyGated()` version. The full script for this example with the data can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_drivers/gru/).
-The data used for this example is the Santa Fe laser dataset [^7] retrieved from [here](https://web.archive.org/web/20160427182805/http://www-psych.stanford.edu/~andreas/Time-Series/SantaFe.html). The data is split to account for a next step prediction.
+To showcase the use of the `GRU()` method, this section will only illustrate the standard `FullyGated()` version. The full script for this example with the data can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_drivers/gru/).
+
+The data used for this example is the Santa Fe laser dataset [^7] retrieved from [here](https://web.archive.org/web/20160427182805/http://www-psych.stanford.edu/%7Eandreas/Time-Series/SantaFe.html). The data is split to account for a next step prediction.
+
```@example gru
using DelimitedFiles
@@ -148,12 +172,13 @@ train_len = 5000
predict_len = 2000
training_input = data[:, 1:train_len]
-training_target = data[:, 2:train_len+1]
-testing_input = data[:,train_len+1:train_len+predict_len]
-testing_target = data[:,train_len+2:train_len+predict_len+1]
+training_target = data[:, 2:(train_len + 1)]
+testing_input = data[:, (train_len + 1):(train_len + predict_len)]
+testing_target = data[:, (train_len + 2):(train_len + predict_len + 1)]
```
-The construction of the ESN proceeds as usual.
+The construction of the ESN proceeds as usual.
+
```@example gru
using ReservoirComputing, Random
@@ -161,22 +186,24 @@ res_size = 300
res_radius = 1.4
Random.seed!(42)
-esn = ESN(training_input;
- reservoir = RandSparseReservoir(res_size, radius=res_radius),
+esn = ESN(training_input;
+ reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = GRU())
```
The default inner reservoir and input layer for the GRU are the same defaults for the `reservoir` and `input_layer` of the ESN. One can use the explicit call if they choose to.
+
```@example gru
-gru = GRU(reservoir=[RandSparseReservoir(res_size),
- RandSparseReservoir(res_size)],
- inner_layer=[DenseLayer(), DenseLayer()])
-esn = ESN(training_input;
- reservoir = RandSparseReservoir(res_size, radius=res_radius),
+gru = GRU(reservoir = [RandSparseReservoir(res_size),
+ RandSparseReservoir(res_size)],
+ inner_layer = [DenseLayer(), DenseLayer()])
+esn = ESN(training_input;
+ reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = gru)
```
The training and prediction can proceed as usual:
+
```@example gru
training_method = StandardRidge(0.0)
output_layer = train(esn, training_target, training_method)
@@ -184,25 +211,27 @@ output = esn(Predictive(testing_input), output_layer)
```
The results can be plotted using Plots.jl
+
```@example gru
using Plots
-plot([testing_target' output'], label=["actual" "predicted"],
- plot_title="Santa Fe Laser",
- titlefontsize=20,
- legendfontsize=12,
- linewidth=2.5,
+plot([testing_target' output'], label = ["actual" "predicted"],
+ plot_title = "Santa Fe Laser",
+ titlefontsize = 20,
+ legendfontsize = 12,
+ linewidth = 2.5,
xtickfontsize = 12,
ytickfontsize = 12,
- size=(1080, 720))
+ size = (1080, 720))
```
It is interesting to see a comparison of the GRU driven ESN and the standard RNN driven ESN. Using the same parameters defined before it is possible to do the following
+
```@example gru
using StatsBase
-esn_rnn = ESN(training_input;
- reservoir = RandSparseReservoir(res_size, radius=res_radius),
+esn_rnn = ESN(training_input;
+ reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = RNN())
output_layer = train(esn_rnn, training_target, training_method)
diff --git a/docs/src/esn_tutorials/hybrid.md b/docs/src/esn_tutorials/hybrid.md
index 2a7b72b7..bf274f01 100644
--- a/docs/src/esn_tutorials/hybrid.md
+++ b/docs/src/esn_tutorials/hybrid.md
@@ -1,48 +1,54 @@
# Hybrid Echo State Networks
+
Following the idea of giving physical information to machine learning models, the hybrid echo state networks [^1] try to achieve this results by feeding model data into the ESN. In this example, it is explained how to create and leverage such models in ReservoirComputing.jl. The full script for this example is available [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/hybrid/hybrid.jl). This example was run on Julia v1.7.2.
## Generating the data
+
For this example, we are going to forecast the Lorenz system. As usual, the data is generated leveraging `DifferentialEquations.jl`:
+
```@example hybrid
using DifferentialEquations
-u0 = [1.0,0.0,0.0]
-tspan = (0.0,1000.0)
+u0 = [1.0, 0.0, 0.0]
+tspan = (0.0, 1000.0)
datasize = 100000
-tsteps = range(tspan[1], tspan[2], length = datasize)
+tsteps = range(tspan[1], tspan[2], length = datasize)
-function lorenz(du,u,p,t)
- p = [10.0,28.0,8/3]
- du[1] = p[1]*(u[2]-u[1])
- du[2] = u[1]*(p[2]-u[3]) - u[2]
- du[3] = u[1]*u[2] - p[3]*u[3]
+function lorenz(du, u, p, t)
+ p = [10.0, 28.0, 8 / 3]
+ du[1] = p[1] * (u[2] - u[1])
+ du[2] = u[1] * (p[2] - u[3]) - u[2]
+ du[3] = u[1] * u[2] - p[3] * u[3]
end
ode_prob = ODEProblem(lorenz, u0, tspan)
ode_sol = solve(ode_prob, saveat = tsteps)
-ode_data =Array(ode_sol)
+ode_data = Array(ode_sol)
train_len = 10000
-input_data = ode_data[:, 1:train_len]
-target_data = ode_data[:, 2:train_len+1]
-test_data = ode_data[:, train_len+1:end][:, 1:1000]
+input_data = ode_data[:, 1:train_len]
+target_data = ode_data[:, 2:(train_len + 1)]
+test_data = ode_data[:, (train_len + 1):end][:, 1:1000]
predict_len = size(test_data, 2)
tspan_train = (tspan[1], ode_sol.t[train_len])
```
## Building the Hybrid Echo State Network
+
To feed the data to the ESN, it is necessary to create a suitable function.
+
```@example hybrid
function prior_model_data_generator(u0, tspan, tsteps, model = lorenz)
- prob = ODEProblem(lorenz, u0, tspan)
+ prob = ODEProblem(lorenz, u0, tspan)
sol = Array(solve(prob, saveat = tsteps))
return sol
end
```
Given the initial condition, time span, and time steps, this function returns the data for the chosen model. Now, using the `Hybrid` method, it is possible to input all this information to the model.
+
```@example hybrid
using ReservoirComputing, Random
Random.seed!(42)
@@ -55,31 +61,35 @@ esn = ESN(input_data,
```
## Training and Prediction
+
The training and prediction of the Hybrid ESN can proceed as usual:
+
```@example hybrid
output_layer = train(esn, target_data, StandardRidge(0.3))
output = esn(Generative(predict_len), output_layer)
```
It is now possible to plot the results, leveraging Plots.jl:
+
```@example hybrid
using Plots
lorenz_maxlyap = 0.9056
-predict_ts = tsteps[train_len+1:train_len+predict_len]
-lyap_time = (predict_ts .- predict_ts[1])*(1/lorenz_maxlyap)
-
-p1 = plot(lyap_time, [test_data[1,:] output[1,:]], label = ["actual" "predicted"],
- ylabel = "x(t)", linewidth=2.5, xticks=false, yticks = -15:15:15);
-p2 = plot(lyap_time, [test_data[2,:] output[2,:]], label = ["actual" "predicted"],
- ylabel = "y(t)", linewidth=2.5, xticks=false, yticks = -20:20:20);
-p3 = plot(lyap_time, [test_data[3,:] output[3,:]], label = ["actual" "predicted"],
- ylabel = "z(t)", linewidth=2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
-
-
-plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
- layout=(3,1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize=15, yguidefontsize=15,
- legendfontsize=12, titlefontsize=20)
+predict_ts = tsteps[(train_len + 1):(train_len + predict_len)]
+lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
+
+p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
+ ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
+p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
+ ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
+p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
+ ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
+
+plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
+ layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
+ yguidefontsize = 15,
+ legendfontsize = 12, titlefontsize = 20)
```
## Bibliography
+
[^1]: Pathak, Jaideep, et al. "_Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model._" Chaos: An Interdisciplinary Journal of Nonlinear Science 28.4 (2018): 041101.
diff --git a/docs/src/esn_tutorials/lorenz_basic.md b/docs/src/esn_tutorials/lorenz_basic.md
index 84b53220..f820a36d 100644
--- a/docs/src/esn_tutorials/lorenz_basic.md
+++ b/docs/src/esn_tutorials/lorenz_basic.md
@@ -1,25 +1,28 @@
- # Lorenz System Forecasting
-
-This example expands on the readme Lorenz system forecasting to better showcase how to use methods and functions provided in the library for Echo State Networks. Here the prediction method used is ```Generative```, for a more detailed explanation of the differences between ```Generative``` and ```Predictive``` please refer to the other examples given in the documentation. The full script for this example is available [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/lorenz_basic/lorenz_basic.jl). This example was run on Julia v1.7.2.
+# Lorenz System Forecasting
+
+This example expands on the readme Lorenz system forecasting to better showcase how to use methods and functions provided in the library for Echo State Networks. Here the prediction method used is `Generative`, for a more detailed explanation of the differences between `Generative` and `Predictive` please refer to the other examples given in the documentation. The full script for this example is available [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/lorenz_basic/lorenz_basic.jl). This example was run on Julia v1.7.2.
## Generating the data
-Starting off the workflow, the first step is to obtain the data. Leveraging ```OrdinaryDiffEq``` it is possible to derive the Lorenz system data in the following way:
+
+Starting off the workflow, the first step is to obtain the data. Leveraging `OrdinaryDiffEq` it is possible to derive the Lorenz system data in the following way:
+
```@example lorenz
using OrdinaryDiffEq
#define lorenz system
-function lorenz!(du,u,p,t)
- du[1] = 10.0*(u[2]-u[1])
- du[2] = u[1]*(28.0-u[3]) - u[2]
- du[3] = u[1]*u[2] - (8/3)*u[3]
+function lorenz!(du, u, p, t)
+ du[1] = 10.0 * (u[2] - u[1])
+ du[2] = u[1] * (28.0 - u[3]) - u[2]
+ du[3] = u[1] * u[2] - (8 / 3) * u[3]
end
#solve and take data
-prob = ODEProblem(lorenz!, [1.0,0.0,0.0], (0.0,200.0))
-data = solve(prob, ABM54(), dt=0.02)
+prob = ODEProblem(lorenz!, [1.0, 0.0, 0.0], (0.0, 200.0))
+data = solve(prob, ABM54(), dt = 0.02)
```
-After obtaining the data, it is necessary to determine the kind of prediction for the model. Since this example will use the ```Generative``` prediction type, this means that the target data will be the next step of the input data. In addition, it is important to notice that the Lorenz system just obtained presents a transient period that is not representative of the general behavior of the system. This can easily be discarded by setting a ```shift``` parameter.
+After obtaining the data, it is necessary to determine the kind of prediction for the model. Since this example will use the `Generative` prediction type, this means that the target data will be the next step of the input data. In addition, it is important to notice that the Lorenz system just obtained presents a transient period that is not representative of the general behavior of the system. This can easily be discarded by setting a `shift` parameter.
+
```@example lorenz
#determine shift length, training length and prediction length
shift = 300
@@ -27,50 +30,56 @@ train_len = 5000
predict_len = 1250
#split the data accordingly
-input_data = data[:, shift:shift+train_len-1]
-target_data = data[:, shift+1:shift+train_len]
-test_data = data[:,shift+train_len+1:shift+train_len+predict_len]
+input_data = data[:, shift:(shift + train_len - 1)]
+target_data = data[:, (shift + 1):(shift + train_len)]
+test_data = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
-It is *important* to notice that the data needs to be formatted in a matrix with the features as rows and time steps as columns as in this example. This is needed even if the time series consists of single values.
+It is *important* to notice that the data needs to be formatted in a matrix with the features as rows and time steps as columns as in this example. This is needed even if the time series consists of single values.
## Building the Echo State Network
-Once the data is ready, it is possible to define the parameters for the ESN and the ```ESN``` struct itself. In this example, the values from [^1] are loosely followed as general guidelines.
+
+Once the data is ready, it is possible to define the parameters for the ESN and the `ESN` struct itself. In this example, the values from [^1] are loosely followed as general guidelines.
+
```@example lorenz
using ReservoirComputing
#define ESN parameters
res_size = 300
res_radius = 1.2
-res_sparsity = 6/300
+res_sparsity = 6 / 300
input_scaling = 0.1
#build ESN struct
-esn = ESN(input_data;
+esn = ESN(input_data;
variation = Default(),
- reservoir = RandSparseReservoir(res_size, radius=res_radius, sparsity=res_sparsity),
- input_layer = WeightedLayer(scaling=input_scaling),
+ reservoir = RandSparseReservoir(res_size, radius = res_radius, sparsity = res_sparsity),
+ input_layer = WeightedLayer(scaling = input_scaling),
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates())
```
-Most of the parameters chosen here mirror the default ones, so a direct call is not necessary. The readme example is identical to this one, except for the explicit call. Going line by line to see what is happening, starting from ```res_size```: this value determines the dimensions of the reservoir matrix. In this case, a size of 300 has been chosen, so the reservoir matrix will be 300 x 300. This is not always the case, since some input layer constructions can modify the dimensions of the reservoir, but in that case, everything is taken care of internally.
+Most of the parameters chosen here mirror the default ones, so a direct call is not necessary. The readme example is identical to this one, except for the explicit call. Going line by line to see what is happening, starting from `res_size`: this value determines the dimensions of the reservoir matrix. In this case, a size of 300 has been chosen, so the reservoir matrix will be 300 x 300. This is not always the case, since some input layer constructions can modify the dimensions of the reservoir, but in that case, everything is taken care of internally.
+
+The `res_radius` determines the scaling of the spectral radius of the reservoir matrix; a proper scaling is necessary to assure the Echo State Property. The default value in the `RandSparseReservoir()` method is 1.0 in accordance with the most commonly followed guidelines found in the literature (see [^2] and references therein). The `sparsity` of the reservoir matrix in this case is obtained by choosing a degree of connections and dividing that by the reservoir size. Of course, it is also possible to simply choose any value between 0.0 and 1.0 to test behaviors for different sparsity values. In this example, the call to the parameters inside `RandSparseReservoir()` was done explicitly to showcase the meaning of each of them, but it is also possible to simply pass the values directly, like so `RandSparseReservoir(1.2, 6/300)`.
-The ```res_radius``` determines the scaling of the spectral radius of the reservoir matrix; a proper scaling is necessary to assure the Echo State Property. The default value in the ```RandSparseReservoir()``` method is 1.0 in accordance with the most commonly followed guidelines found in the literature (see [^2] and references therein). The ```sparsity``` of the reservoir matrix in this case is obtained by choosing a degree of connections and dividing that by the reservoir size. Of course, it is also possible to simply choose any value between 0.0 and 1.0 to test behaviors for different sparsity values. In this example, the call to the parameters inside ```RandSparseReservoir()``` was done explicitly to showcase the meaning of each of them, but it is also possible to simply pass the values directly, like so ```RandSparseReservoir(1.2, 6/300)```.
+The value of `input_scaling` determines the upper and lower bounds of the uniform distribution of the weights in the `WeightedLayer()`. Like before, this value can be passed either as an argument or as a keyword argument `WeightedLayer(0.1)`. The value of 0.1 represents the default. The default input layer is the `DenseLayer`, a fully connected layer. The details of the weighted version can be found in [^3], for this example, this version returns the best results.
-The value of ```input_scaling``` determines the upper and lower bounds of the uniform distribution of the weights in the ```WeightedLayer()```. Like before, this value can be passed either as an argument or as a keyword argument ```WeightedLayer(0.1)```. The value of 0.1 represents the default. The default input layer is the ```DenseLayer```, a fully connected layer. The details of the weighted version can be found in [^3], for this example, this version returns the best results.
+The reservoir driver represents the dynamics of the reservoir. In the standard ESN definition, these dynamics are obtained through a Recurrent Neural Network (RNN), and this is reflected by calling the `RNN` driver for the `ESN` struct. This option is set as the default, and unless there is the need to change parameters, it is not needed. The full equation is the following:
-The reservoir driver represents the dynamics of the reservoir. In the standard ESN definition, these dynamics are obtained through a Recurrent Neural Network (RNN), and this is reflected by calling the ```RNN``` driver for the ```ESN``` struct. This option is set as the default, and unless there is the need to change parameters, it is not needed. The full equation is the following:
```math
\textbf{x}(t+1) = (1-\alpha)\textbf{x}(t) + \alpha \cdot \text{tanh}(\textbf{W}\textbf{x}(t)+\textbf{W}_{\text{in}}\textbf{u}(t))
```
-where ``α`` represents the leaky coefficient, and tanh can be any activation function. Also, ``\textbf{x}`` represents the state vector, ``\textbf{u}`` the input data, and ``\textbf{W}, \textbf{W}_{\text{in}}`` are the reservoir matrix and input matrix, respectively. The default call to the RNN in the library is the following ```RNN(;activation_function=tanh, leaky_coefficient=1.0)```, where the meaning of the parameters is clear from the equation above. Instead of the hyperbolic tangent, any activation function can be used, either leveraging external libraries such as ```NNlib``` or creating a custom one.
-The final calls are modifications to the states in training or prediction. The default calls, depicted in the example, do not make any modifications to the states. This is the safest bet if one is not sure how these work. The ```nla_type``` applies a non-linear algorithm to the states, while the ```states_type``` can expand them by concatenating them with the input data, or padding them by concatenating a constant value to all the states. More in depth descriptions of these parameters are given in other examples in the documentation.
+where ``α`` represents the leaky coefficient, and tanh can be any activation function. Also, ``\textbf{x}`` represents the state vector, ``\textbf{u}`` the input data, and ``\textbf{W}, \textbf{W}_{\text{in}}`` are the reservoir matrix and input matrix, respectively. The default call to the RNN in the library is the following `RNN(;activation_function=tanh, leaky_coefficient=1.0)`, where the meaning of the parameters is clear from the equation above. Instead of the hyperbolic tangent, any activation function can be used, either leveraging external libraries such as `NNlib` or creating a custom one.
+
+The final calls are modifications to the states in training or prediction. The default calls, depicted in the example, do not make any modifications to the states. This is the safest bet if one is not sure how these work. The `nla_type` applies a non-linear algorithm to the states, while the `states_type` can expand them by concatenating them with the input data, or padding them by concatenating a constant value to all the states. More in depth descriptions of these parameters are given in other examples in the documentation.
## Training and Prediction
+
Now that the ESN has been created and all the parameters have been explained, it is time to proceed with the training. The full call of the readme example follows this general idea:
+
```@example lorenz
#define training method
training_method = StandardRidge(0.0)
@@ -79,37 +88,41 @@ training_method = StandardRidge(0.0)
output_layer = train(esn, target_data, training_method)
```
-The training returns an ```OutputLayer``` struct containing the trained output matrix and other needed for the prediction. The necessary elements in the ```train()``` call are the ```ESN``` struct created in the previous step and the ```target_data```, which in this case is the one step ahead evolution of the Lorenz system. The training method chosen in this example is the standard one, so an equivalent way of calling the ```train``` function here is ```output_layer = train(esn, target_data)``` like the readme basic version. Likewise, the default value for the ridge regression parameter is set to zero, so the actual default training is Ordinary Least Squares regression. Other training methods are available and will be explained in the following examples.
+The training returns an `OutputLayer` struct containing the trained output matrix and other needed for the prediction. The necessary elements in the `train()` call are the `ESN` struct created in the previous step and the `target_data`, which in this case is the one step ahead evolution of the Lorenz system. The training method chosen in this example is the standard one, so an equivalent way of calling the `train` function here is `output_layer = train(esn, target_data)` like the readme basic version. Likewise, the default value for the ridge regression parameter is set to zero, so the actual default training is Ordinary Least Squares regression. Other training methods are available and will be explained in the following examples.
+
+Once the `OutputLayer` has been obtained, the prediction can be done following this procedure:
-Once the ```OutputLayer``` has been obtained, the prediction can be done following this procedure:
```@example lorenz
output = esn(Generative(predict_len), output_layer)
```
-both the training method and the output layer are needed in this call. The number of steps for the prediction must be specified in the ```Generative``` method. The output results are given in a matrix.
+
+both the training method and the output layer are needed in this call. The number of steps for the prediction must be specified in the `Generative` method. The output results are given in a matrix.
!!! info "Saving the states during prediction"
+
While the states are saved in the `ESN` struct for the training, for the prediction they are not saved by default. To inspect the states, it is necessary to pass the boolean keyword argument `save_states` to the prediction call, in this example using `esn(... ; save_states=true)`. This returns a tuple `(output, states)` where `size(states) = res_size, prediction_len`
-To inspect the results, they can easily be plotted using an external library. In this case, ```Plots``` is adopted:
+To inspect the results, they can easily be plotted using an external library. In this case, `Plots` is adopted:
+
```@example lorenz
using Plots, Plots.PlotMeasures
ts = 0.0:0.02:200.0
lorenz_maxlyap = 0.9056
-predict_ts = ts[shift+train_len+1:shift+train_len+predict_len]
-lyap_time = (predict_ts .- predict_ts[1])*(1/lorenz_maxlyap)
-
-p1 = plot(lyap_time, [test_data[1,:] output[1,:]], label = ["actual" "predicted"],
- ylabel = "x(t)", linewidth=2.5, xticks=false, yticks = -15:15:15);
-p2 = plot(lyap_time, [test_data[2,:] output[2,:]], label = ["actual" "predicted"],
- ylabel = "y(t)", linewidth=2.5, xticks=false, yticks = -20:20:20);
-p3 = plot(lyap_time, [test_data[3,:] output[3,:]], label = ["actual" "predicted"],
- ylabel = "z(t)", linewidth=2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
-
-
-plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
- layout=(3,1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize=15, yguidefontsize=15,
- legendfontsize=12, titlefontsize=20)
+predict_ts = ts[(shift + train_len + 1):(shift + train_len + predict_len)]
+lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
+
+p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
+ ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
+p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
+ ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
+p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
+ ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
+
+plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
+ layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
+ yguidefontsize = 15,
+ legendfontsize = 12, titlefontsize = 20)
```
## Bibliography
@@ -117,4 +130,3 @@ plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
[^1]: Pathak, Jaideep, et al. "_Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.12 (2017): 121102.
[^2]: Lukoševičius, Mantas. "_A practical guide to applying echo state networks._" Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012. 659-686.
[^3]: Lu, Zhixin, et al. "_Reservoir observers: Model-free inference of unmeasured variables in chaotic systems._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.4 (2017): 041102.
-
diff --git a/docs/src/general/different_training.md b/docs/src/general/different_training.md
index 231389c1..bb92680c 100644
--- a/docs/src/general/different_training.md
+++ b/docs/src/general/different_training.md
@@ -1,5 +1,7 @@
# Changing Training Algorithms
+
Notably Echo State Networks have been trained with Ridge Regression algorithms, but the range of useful algorithms to use is much greater. In this section of the documentation, it is possible to explore how to use other training methods to obtain the readout layer. All the methods implemented in ReservoirComputing.jl can be used for all models in the library, not only ESNs. The general workflow illustrated in this section will be based on a dummy RC model `my_model = MyModel(...)` that needs training to obtain the readout layer. The training is done as follows:
+
```julia
training_algo = TrainingAlgo()
readout_layer = train(my_model, train_data, training_algo)
@@ -8,40 +10,23 @@ readout_layer = train(my_model, train_data, training_algo)
In this section, it is possible to explore how to properly build the `training_algo` and all the possible choices available. In the example section of the documentation it will be provided copy-pasteable code to better explore the training algorithms and their impact on the model.
## Linear Models
-The library includes a standard implementation of ridge regression, callable using `StandardRidge(regularization_coeff)` where the default value for the regularization coefficient is set to zero. This is also the default model called when no model is specified in `train()`. This makes the default call for training `train(my_model, train_data)` use Ordinary Least Squares (OLS) for regression.
-Leveraging [MLJLinearModels](https://juliaai.github.io/MLJLinearModels.jl/stable/) it is possible to expand the choices of linear models used for the training. The wrappers provided are structured in the following way:
-```julia
-struct LinearModel
- regression
- solver
- regression_kwargs
-end
-```
-to call the ridge regression using the MLJLinearModels APIs, one can use `LinearModel(;regression=LinearRegression)`. It is also possible to use a specific solver, by calling `LinearModel(regression=LinearRegression, solver=Analytical())`. For all the available solvers, please refer to the [MLJLinearModels documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/models/). To change the regularization coefficient in the ridge example, using for example `lambda = 0.1`, it is needed to pass it in the `regression_kwargs` like so `LinearModel(;regression=LinearRegression, solver=Analytical(), regression_kwargs=(lambda=lambda))`. The nomenclature of the coefficients must follow the MLJLinearModels APIs, using `lambda, gamma` for `LassoRegression` and `delta, lambda, gamma` for `HuberRegression`. Again, please check the [relevant documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/api/) if in doubt. When using MLJLinearModels based regressors, do remember to specify `using MLJLinearModels`.
+The library includes a standard implementation of ridge regression, callable using `StandardRidge(regularization_coeff)`. The default regularization coefficient is set to zero. This is also the default model called when no model is specified in `train()`. This makes the default call for training `train(my_model, train_data)` use Ordinary Least Squares (OLS) for regression.
+
+Leveraging [MLJLinearModels](https://juliaai.github.io/MLJLinearModels.jl/stable/) you can expand your choices of linear models for training. The wrappers provided follow this structure:
-## Gaussian Processes
-Another way to obtain the readout layer is possible using Gaussian regression. This is provided through a wrapper of [GaussianProcesses](http://stor-i.github.io/GaussianProcesses.jl/latest/) structured in the following way:
```julia
-struct GaussianProcess
- mean
- kernel
- lognoise
- optimize
- optimizer
+struct LinearModel
+ regression::Any
+ solver::Any
+ regression_kwargs::Any
end
```
-While it is necessary to specify a `mean` and a `kernel`, the other defaults are `lognoise=-2, optimize=false, optimizer=Optim.LBFGS()`. For the choice of means and kernels, please refer to the proper documentation, [here](http://stor-i.github.io/GaussianProcesses.jl/latest/mean/) and [here](http://stor-i.github.io/GaussianProcesses.jl/latest/kernels/), respectively.
-Building on the simple example given in the GaussianProcesses documentation, it is possible to build an intuition of how to use these algorithms for training ReservoirComputing.jl models.
-```julia
-mZero = MeanZero() #Zero mean function
-kern = SE(0.0,0.0) #Squared exponential kernel (note that hyperparameters are on the log scale)
-logObsNoise = -1.0
+To call the ridge regression using the MLJLinearModels APIs, you can use `LinearModel(;regression=LinearRegression)`. You can also choose a specific solver by calling, for example, `LinearModel(regression=LinearRegression, solver=Analytical())`. For all the available solvers, please refer to the [MLJLinearModels documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/models/).
-gp = GaussianProcess(mZero, kern, lognoise=logObsNoise)
-```
-Like in the previous case, if one uses GaussianProcesses based regressors, it is necessary to specify `using GaussianProcesses`. Additionally, if the optimizer chosen is from an external package, i.e. Optim, that package needs to be used in the script as well by adding `using Optim`.
+To change the regularization coefficient in the ridge example, using for example `lambda = 0.1`, it is needed to pass it in the `regression_kwargs` like so `LinearModel(;regression=LinearRegression, solver=Analytical(), regression_kwargs=(lambda=lambda))`. The nomenclature of the coefficients must follow the MLJLinearModels APIs, using `lambda, gamma` for `LassoRegression` and `delta, lambda, gamma` for `HuberRegression`. Again, please check the [relevant documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/api/) if in doubt. When using MLJLinearModels based regressors, do remember to specify `using MLJLinearModels`.
## Support Vector Regression
-Contrary to the `LinearModel`s and `GaussianProcess`es, no wrappers are needed for support vector regression. By using [LIBSVM.jl](https://github.com/JuliaML/LIBSVM.jl), LIBSVM wrappers in Julia, it is possible to call both `epsilonSVR()` or `nuSVR()` directly in `train()`. For the full range of kernels provided and the parameters to call, we refer the user to the official [documentation](https://www.csie.ntu.edu.tw/~cjlin/libsvm/). Like before, if one intends to use LIBSVM regressors, it is necessary to specify `using LIBSVM`.
+
+Contrary to the `LinearModel`s, no wrappers are needed for support vector regression. By using [LIBSVM.jl](https://github.com/JuliaML/LIBSVM.jl), LIBSVM wrappers in Julia, it is possible to call both `epsilonSVR()` or `nuSVR()` directly in `train()`. For the full range of kernels provided and the parameters to call, we refer the user to the official [documentation](https://www.csie.ntu.edu.tw/%7Ecjlin/libsvm/). Like before, if one intends to use LIBSVM regressors, it is necessary to specify `using LIBSVM`.
diff --git a/docs/src/general/predictive_generative.md b/docs/src/general/predictive_generative.md
index 0c61f08c..c3be7b26 100644
--- a/docs/src/general/predictive_generative.md
+++ b/docs/src/general/predictive_generative.md
@@ -1,10 +1,17 @@
# Generative vs Predictive
-The library provides two different methods for prediction, denoted as `Predictive()` and `Generative()`, following the two major applications of Reservoir Computing models found in the literature. Both of these methods are given as arguments for the trained model. While copy-pasteable example swill be provided further on in the documentation, it is better to clarify the difference early on to focus more on the library implementation going forward.
+
+The library provides two different methods for prediction, denoted as `Predictive()` and `Generative()`. These methods correspond to the two major applications of Reservoir Computing models found in the literature. This section aims to clarify the differences between these two methods before providing further details on their usage in the library.
## Predictive
-In the first method, the user can use Reservoir Computing models similarly as standard Machine Learning models. This means using a set of features as input and a set of labels as outputs. In this case, the features and labels can be vectors of different dimensions, as ``X=\{x_1,...,x_n\} \ x_i \in \mathbb{R}^{N}`` and ``Y=\{y_1,...,y_n\} \ y_i \in \mathbb{R}^{M}`` where ``X`` is the feature set and ``Y`` the label set. Given the difference in dimensionality for the prediction call, it will be needed to feed to the function the feature set to be labeled, for example by calling `Predictive(X)` using the set given in this example.
-!this allows for one step ahead or h steps ahead prediction.
+In the first method, users can utilize Reservoir Computing models in a manner similar to standard Machine Learning models. This involves using a set of features as input and a set of labels as outputs. In this case, both the feature and label sets can consist of vectors of different dimensions. Specifically, let's denote the feature set as ``X=\{x_1,...,x_n\}`` where ``x_i \in \mathbb{R}^{N}``, and the label set as ``Y=\{y_1,...,y_n\}`` where ``y_i \in \mathbb{R}^{M}``.
+
+To make predictions using this method, you need to provide the feature set that you want to predict the labels for. For example, you can call `Predictive(X)` using the feature set ``X`` as input. This method allows for both one-step-ahead and multi-step-ahead predictions.
## Generative
-The generative method allows the user to extend the forecasting capabilities of the model, letting the predicted results to be fed back into the model to generate the next prediction. By doing so, the model can run autonomously, without any feature dataset as input. The call for this model needs only the number of steps that the user intends to forecast, for example calling `Generative(100)` to generate one hundred time steps.
+
+The generative method provides a different approach to forecasting with Reservoir Computing models. It enables you to extend the forecasting capabilities of the model by allowing predicted results to be fed back into the model to generate the next prediction. This autonomy allows the model to make predictions without the need for a feature dataset as input.
+
+To use the generative method, you only need to specify the number of time steps that you intend to forecast. For instance, you can call `Generative(100)` to generate predictions for the next one hundred time steps.
+
+The key distinction between these methods lies in how predictions are made. The predictive method relies on input feature sets to make predictions, while the generative method allows for autonomous forecasting by feeding predicted results back into the model.
diff --git a/docs/src/general/states_variation.md b/docs/src/general/states_variation.md
index 521fbdad..a1b0dab5 100644
--- a/docs/src/general/states_variation.md
+++ b/docs/src/general/states_variation.md
@@ -1,38 +1,53 @@
# Altering States
-In every ReservoirComputing model is possible to perform some alteration on the states in the training stage. Depending on the chosen modification, this can improve the results of the prediction. Or more simply, they can be used to reproduce results in the literature. The alterations are divided into two possibilities: the first concerns padding or extending the states, and the second concerns non-linear algorithms performed over the states.
+
+In ReservoirComputing models, it's possible to perform alterations on the reservoir states during the training stage. These alterations can improve prediction results or replicate results found in the literature. Alterations are categorized into two possibilities: padding or extending the states, and applying non-linear algorithms to the states.
## Padding and Extending States
-Extending the states means appending to them the corresponding input values. If ``\textbf{x}(t)`` is the reservoir state at time t corresponding to the input ``\textbf{u}(t)`` the extended state will be represented as `` [\textbf{x}(t); \textbf{u}(t)]`` where ``[;]`` is intended as vertical concatenation. This procedure is, for example, used in [Jaeger's Scholarpedia](http://www.scholarpedia.org/article/Echo_state_network) description of Echo State Networks. The extension of the states can be obtained in every ReservoirComputing.jl model by using the keyword argument `states_type` and calling the method `ExtendedStates()`. No argument is needed.
-Padding the states means appending a constant value, 1.0 for example, to each state. Using the notation introduced before, we can define the padded states as ``[\textbf{x}(t); 1.0]``. This approach is detailed in the [seminal guide](https://mantas.info/get-publication/?f=Practical_ESN.pdf) to Echo State Networks by Mantas Lukoševičius. By using the keyword argument `states_type` the user can call the method `PaddedStates(padding)` where `padding` represents the value that will be concatenated to the states. As default, the value is set to unity, so the majority of the time, calling `PaddedStates()` will suffice.
+### Extending States
+
+Extending the states involves appending the corresponding input values to the reservoir states. If \(\textbf{x}(t)\) represents the reservoir state at time \(t\) corresponding to the input \(\textbf{u}(t)\), the extended state is represented as \([\textbf{x}(t); \textbf{u}(t)]\), where \([;]\) denotes vertical concatenation. This procedure is commonly used in Echo State Networks and is described in [Jaeger's Scholarpedia](http://www.scholarpedia.org/article/Echo_state_network). You can extend the states in every ReservoirComputing.jl model by using the `states_type` keyword argument and calling the `ExtendedStates()` method. No additional arguments are needed.
+
+### Padding States
-Though not easily found in the literature, it is also possible to pad the extended states by using the method `PaddedExtendedStates(padding)` that has unity as `padding` default as well.
+Padding the states involves appending a constant value, such as 1.0, to each state. In the notation introduced earlier, padded states can be represented as \([\textbf{x}(t); 1.0]\). This approach is detailed in the [seminal guide](https://mantas.info/get-publication/?f=Practical_ESN.pdf) to Echo State Networks by Mantas Lukoševičius. To pad the states, you can use the `states_type` keyword argument and call the `PaddedStates(padding)` method, where `padding` represents the value to be concatenated to the states. By default, the padding value is set to 1.0, so most of the time, calling `PaddedStates()` will suffice.
-Of course, it is also possible to not apport any of these changes to the states by calling `StandardStates()`. This is also the default choice for the states.
+Additionally, you can pad the extended states by using the `PaddedExtendedStates(padding)` method, which also has a default padding value of 1.0.
+
+You can choose not to apply any of these changes to the states by calling `StandardStates()`, which is the default choice for the states.
## Non-Linear Algorithms
-First introduced in [^1] and expanded in [^2] these are nonlinear combinations of the columns of the matrix states. There are three such algorithms implemented. Using the keyword argument `nla_type` it is possible to choose in every model in ReservoirComputing.jl the specific non-linear algorithm to use. The default value is set to `NLADefault()`, where no non-linear algorithm takes place.
-Following the nomenclature used in [^2], the algorithms can be called as `NLAT1()`, `NLAT2()` and `NLAT3()`. To better explain what they do, let ``\textbf{x}_{i, j}`` be elements of the state matrix, with ``i=1,...,T \ j=1,...,N`` where ``T`` is the length of the training and ``N`` is the reservoir size.
+First introduced in [^1] and expanded in [^2], non-linear algorithms are nonlinear combinations of the columns of the matrix states. There are three such algorithms implemented in ReservoirComputing.jl, and you can choose which one to use with the `nla_type` keyword argument. The default value is set to `NLADefault()`, which means no non-linear algorithm is applied.
+
+The available non-linear algorithms are:
+
+ - `NLAT1()`
+ - `NLAT2()`
+ - `NLAT3()`
+
+These algorithms perform specific operations on the reservoir states. To provide a better understanding of what they do, let ``\textbf{x}_{i, j}`` be elements of the state matrix, with ``i=1,...,T \ j=1,...,N`` where ``T`` is the length of the training and ``N`` is the reservoir size.
**NLAT1**
+
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \times \textbf{x}_{i,j} \ \ \text{if \textit{j} is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is even}
```
**NLAT2**
+
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j-1} \times \textbf{x}_{i,j-2} \ \ \text{if \textit{j} > 1 is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is 1 or even}
```
**NLAT3**
+
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j-1} \times \textbf{x}_{i,j+1} \ \ \text{if \textit{j} > 1 is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is 1 or even}
```
[^1]: Pathak, Jaideep, et al. "_Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.12 (2017): 121102.
-
[^2]: Chattopadhyay, Ashesh, Pedram Hassanzadeh, and Devika Subramanian. "_Data-driven predictions of a multiscale Lorenz 96 chaotic system using machine-learning methods: reservoir computing, artificial neural network, and long short-term memory network._" Nonlinear Processes in Geophysics 27.3 (2020): 373-389.
diff --git a/docs/src/index.md b/docs/src/index.md
index e2add232..ac8e1f66 100644
--- a/docs/src/index.md
+++ b/docs/src/index.md
@@ -1,103 +1,53 @@
# ReservoirComputing.jl
-ReservoirComputing.jl provides an efficient, modular, and easy to use implementation of Reservoir Computing models such as Echo State Networks (ESNs). Reservoir Computing (RC) is an umbrella term used to describe a family of models such as ESNs and Liquid State Machines (LSMs). The key concept is to expand the input data into a higher dimension and use regression to train the model; in some ways, Reservoir Computers can be considered similar to kernel methods.
-
+ReservoirComputing.jl is a versatile and user-friendly Julia package designed for the implementation of advanced Reservoir Computing models, such as Echo State Networks (ESNs). Central to Reservoir Computing is the expansion of input data into a higher-dimensional space, leveraging regression techniques for effective model training. This approach bears resemblance to kernel methods, offering a unique perspective in machine learning. ReservoirComputing.jl offers a modular design, ensuring both ease of use for newcomers and flexibility for advanced users, establishing it as a key tool for innovative computing solutions.
!!! info "Introductory material"
- This library assumes some basic knowledge of Reservoir Computing. For a good introduction, we suggest the following papers: the first two are the seminal papers about ESN and LSM, the others are in-depth review papers that should cover all the needed information. For the majority of the algorithms implemented in this library, we cited in the documentation the original work introducing them. If you ever have doubts about a method or a function, just type ```? function``` in the Julia REPL to read the relevant notes.
-
- * Jaeger, Herbert: The “echo state” approach to analyzing and training recurrent neural networks-with an erratum note.
- * Maass W, Natschläger T, Markram H: Real-time computing without stable states: a new framework for neural computation based on perturbations.
- * Lukoševičius, Mantas: A practical guide to applying echo state networks." Neural networks: Tricks of the trade.
- * Lukoševičius, Mantas, and Herbert Jaeger: Reservoir computing approaches to recurrent neural network training.
+ This library assumes some basic knowledge of Reservoir Computing. For a good introduction, we suggest the following papers: the first two are the seminal papers about ESN and LSM, the others are in-depth review papers that should cover all the needed information. For the majority of the algorithms implemented in this library we cited in the documentation the original work introducing them. If you ever are in doubt about a method or a function just type `? function` in the Julia REPL to read the relevant notes.
+
+ - Jaeger, Herbert: The “echo state” approach to analyzing and training recurrent neural networks-with an erratum note.
+ - Maass W, Natschläger T, Markram H: Real-time computing without stable states: a new framework for neural computation based on perturbations.
+ - Lukoševičius, Mantas: A practical guide to applying echo state networks." Neural networks: Tricks of the trade.
+ - Lukoševičius, Mantas, and Herbert Jaeger: Reservoir computing approaches to recurrent neural network training.
+
!!! info "Performance tip"
- For faster computations on the CPU, it is suggested to add `using MKL` to the script. For clarity's sake, this library will not be indicated under every example in the documentation.
+
+ For faster computations on the CPU it is suggested to add `using MKL` to the script. For clarity's sake this library will not be indicated under every example in the documentation.
+
## Installation
-To install ReservoirComputing.jl, use the Julia package manager:
+To install ReservoirComputing.jl, ensure you have Julia version 1.6 or higher. Follow these steps:
+
+ 1. Open the Julia command line.
+ 2. Enter the Pkg REPL mode by pressing ].
+ 3. Type add ReservoirComputing and press Enter.
+
+For a more customized installation or to contribute to the package, consider cloning the repository:
```julia
using Pkg
-Pkg.add("ReservoirComputing")
+Pkg.clone("https://github.com/SciML/ReservoirComputing.jl.git")
```
-The support for this library is for Julia v1.6 or greater.
+
+or `dev` the package.
## Features Overview
-This library provides multiple ways of training the chosen RC model. More specifically, the available algorithms are:
-- ```StandardRidge```: a naive implementation of Ridge Regression. The default choice for training.
-- ```LinearModel```: a wrap around [MLJLinearModels](https://juliaai.github.io/MLJLinearModels.jl/stable/).
-- ```LIBSVM.AbstractSVR```: a direct call of [LIBSVM](https://github.com/JuliaML/LIBSVM.jl) regression methods.
-
-Also provided are two different ways of making predictions using RC:
-- ```Generative```: the algorithm uses the prediction of the model in the previous step to continue the prediction. It only needs the number of steps as input.
-- ```Predictive```: standard Machine Learning type of prediction. Given the features, the RC model will return the label/prediction.
-
-It is possible to modify the RC obtained states in the training and prediction steps using the following:
-- ```StandardStates```: default choice, no changes will be made to the states.
-- ```ExtendedStates```: the states are extended using a vertical concatenation, with the input data.
-- ```PaddedStates```: the states are padded using a vertical concatenation with the chosen padding value.
-- ```PaddedExtendedStates```: a combination of the first two. First, the states are extended and then padded.
-
-In addition, another modification is possible through the choice of non-linear algorithms:
-- ```NLADefault```: default choice, no changes will be made to the states.
-- ```NLAT1```
-- ```NLAT2```
-- ```NLAT3```
-
-### Echo State Networks
-For ESNs the following input layers are implemented :
-- ```WeightedLayer```: weighted layer matrix with weights sampled from a uniform distribution.
-- ```DenseLayer```: dense layer matrix with weights sampled from a uniform distribution.
-- ```SparseLayer```: sparse layer matrix with weights sampled from a uniform distribution.
-- ```MinimumLayer```: matrix with constant weights and weight sign decided following one of the two:
- - ```BernoulliSample```
- - ```IrrationalSample```
-- ```InformedLayer```: special kin of weighted layer matrix for Hybrid ESNs.
-
-The package also contains multiple implementations of Reservoirs:
-- ```RandSparseReservoir```: random sparse matrix with scaling of spectral radius
-- ```PseudoSVDReservoir```: Pseudo SVD construction of a random sparse matrix
-- ```DelayLineReservoir```: minimal matrix with chosen weights
-- ```DelayLineBackwardReservoir```: minimal matrix with chosen weights
-- ```SimpleCycleReservoir```: minimal matrix with chosen weights
-- ```CycleJumpsReservoir```: minimal matrix with chosen weights
-
-In addition, multiple ways of driving the reservoir states are also provided:
-- ```RNN```: standard Recurrent Neural Network driver.
-- ```MRNN```: Multiple RNN driver, it consists of a linear combination of RNNs
-- ```GRU```: gated Recurrent Unit driver, with all the possible GRU variants available:
- - ```FullyGated```
- - ```Minimal```
-
-A hybrid version of the model is also available through ```Hybrid```
-
-### Reservoir Computing with Cellular Automata
-The package provides also an implementation of Reservoir Computing models based on one dimensional Cellular Automata through the ```RECA``` call. For the moment, the only input encoding available (an input encoding plays a similar role to the input matrix for ESNs) is a random mapping, called through ```RandomMapping```.
-
-All the training methods described above can be used, as can all the modifications to the states. Both prediction methods are also possible in theory, although in the literature only ```Predictive``` tasks have been explored.
+ - **Multiple Training Algorithms**: Supports Ridge Regression, Linear Models, and LIBSVM regression methods for Reservoir Computing models.
+ - **Diverse Prediction Methods**: Offers both generative and predictive methods for Reservoir Computing predictions.
+ - **Modifiable Training and Prediction**: Allows modifications in Reservoir Computing states, such as state extension, padding, and combination methods.
+ - **Non-linear Algorithm Options**: Includes options for non-linear modifications in algorithms.
+ - **Echo State Networks (ESNs)**: Features various input layers, reservoirs, and methods for driving ESN reservoir states.
+ - **Cellular Automata-Based Reservoir Computing**: Introduces models based on one-dimensional Cellular Automata for Reservoir Computing.
## Contributing
- - Please refer to the
- [SciML ColPrac: Contributor's Guide on Collaborative Practices for Community Packages](https://github.com/SciML/ColPrac/blob/master/README.md)
- for guidance on PRs, issues, and other matters relating to contributing to SciML.
-
- - See the [SciML Style Guide](https://github.com/SciML/SciMLStyle) for common coding practices and other style decisions.
- - There are a few community forums:
-
- + The #diffeq-bridged and #sciml-bridged channels in the
- [Julia Slack](https://julialang.org/slack/)
- + The #diffeq-bridged and #sciml-bridged channels in the
- [Julia Zulip](https://julialang.zulipchat.com/#narrow/stream/279055-sciml-bridged)
- + On the [Julia Discourse forums](https://discourse.julialang.org)
- + See also [SciML Community page](https://sciml.ai/community/)
-
+Contributions to ReservoirComputing.jl are highly encouraged and appreciated. Whether it's through implementing new RC model variations, enhancing documentation, adding examples, or any improvement, your contribution is valuable. We welcome posts of relevant papers or ideas in the issues section. For deeper insights into the library's functionality, the API section in the documentation is a great resource. For any queries not suited for issues, please reach out to the lead developers via Slack or email.
## Citing
-If you use this library in your work, please cite:
+If you use ReservoirComputing.jl in your work, we kindly ask you to cite it. Here is the BibTeX entry for your convenience:
```bibtex
@article{JMLR:v23:22-0611,
@@ -113,36 +63,46 @@ If you use this library in your work, please cite:
```
## Reproducibility
+
```@raw html
The documentation of this SciML package was built using these direct dependencies,
```
+
```@example
using Pkg # hide
Pkg.status() # hide
```
+
```@raw html
and using this machine and Julia version.
```
+
```@example
using InteractiveUtils # hide
versioninfo() # hide
```
+
```@raw html
A more complete overview of all dependencies and their versions is also provided.
```
+
```@example
using Pkg # hide
-Pkg.status(;mode = PKGMODE_MANIFEST) # hide
+Pkg.status(; mode = PKGMODE_MANIFEST) # hide
```
+
```@raw html