| 有限的状态集合 | |
|---|---|
| 有限的动作集合 | |
| 马尔科夫转移矩阵 | |
| **奖励函数,$\mathcal{R}=\mathbb{E}[R_{t+1} | |
| 折扣因子 |
如果一个过程具有如下性质,则该过程具有Markov Property: $$ \mathbb{P} [S_{t+1}|S_t]=\mathbb{P}[S_{t+1}|S_t,S_{t-1},..,S_1] $$ 也就是说,当前状态只与前一个状态有关,而与历史的状态无关,但从递推关系上,历史的状态又通过递推形式传递到当前状态,隐含了历史信息。
马尔可夫过程中的一个状态转换成另一个状态的概率表示为: $$ \mathcal{P}{SS'}=\mathbb{P}[S{t+1}=S'|S_t=S] $$ 那么马尔科夫转移矩阵则表示所有状态之间的转换关系: $$ \mathcal{P}=\begin{pmatrix} \mathcal{P}{11} & \cdots &\mathcal{P}{1n}\ \vdots&\ddots&\vdots\ \mathcal{P}{n1}&\cdots&\mathcal{P}{nn} \end{pmatrix} $$ 马尔可夫过程是一个$(\mathcal{S},\mathcal{P})$的元组
马尔可夫奖励过程是一个$(\mathcal{S},\mathcal{P},\mathcal{R},\mathcal{\gamma})$,MRP的奖励依赖于当前的state,而不同于MDP奖励是依赖于当前状态和动作选择。
注意事项与一些说明:
-
奖励是延迟性的,也就是只有过了当前状态,环境才会反馈agent奖励
-
回报:在MP过程中我们寻求的最大期望回报,记为$G_t$。引入了折扣因子的收益总和: $$ G_t = R_{t+1}+\gamma R_{t+2}+\cdots = \sum_{k=0}^{\infty}\gamma^k R_{t+k+1} $$
-
分幕式和持续式任务的区别:分幕(episodes)式的任务有很多子序列,比如一个游戏中的回合一样,会在有限时刻终止,上述回报会在某个时刻终止,而不会无穷远停止;而持续性任务一般只有一个序列,而且序列是无穷的,例如机器人的长期运行。
-
价值函数:价值函数是状态(状态-动作)的函数,评价当前状态的好坏,同时也是回报的期望收益。在MRP中, $$ \begin{align} v(s)&=\mathbb{E}[G_t|S_t=s]\ &=\mathbb{E}[ R_{t+1}+\gamma R_{t+2}+\cdots |S_t=s]\ &=\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\ & = \mathbb{E}[R_{t+1}+\gamma v(S_{t+1})|S_t=s)] \end{align} $$ 最终推导出来的是MRP的贝尔曼方程:
$$ v=R+\gamma \mathcal{P} v $$
MDP是一个$(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma})$的元组,MDP奖励是依赖于当前状态和动作选择。
一些说明:
-
引入动作之后,MDP出现策略和动作价值函数
-
策略$\pi(a|s)=\mathcal{P}[A_t=a|S_t=s]$
-
价值函数的变化: $$ v_{\pi}(s)=\mathbb{E}{\pi}[G_t|S_t=s]\ q{\pi}(s,a)=\mathbb{E}_{\pi}[G_t|S_t=s,A_t=a] $$ 以上分别是策略$\pi$的状态价值函数和动作价值函数
-
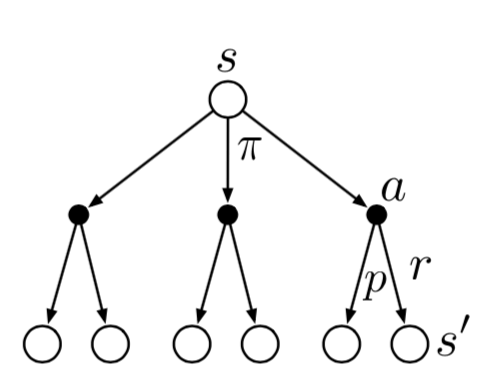
由下图的状态函数回溯图得到状态价值函数的贝尔曼方程: $$ \begin{align} v_{\pi}(s)&=\mathbb{E}{\pi}[G_t|S_t=s]\ &=\mathbb{E}{\pi}[R_{t+1}+\gamma G_{t+1}|S_t=s]\ &=\sum_{a} \pi(a|s) \sum_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')] \end{align} $$
-
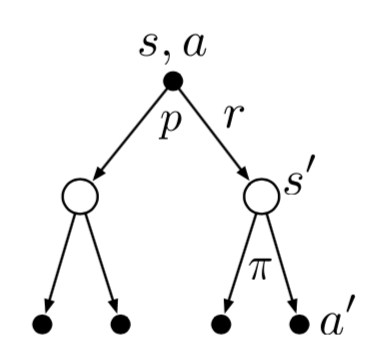
由下图的动作价值函数的回溯图得到动作价值函数的贝尔曼方程: $$ \begin{align} q_{\pi}(s,a)&=\mathbb{E}{\pi}[G_t|S_t=s,A_t=a]\ &=\sum{s',r} p(s',r|s,a) [r+\gamma \sum_{a'}\pi (a'|s')q_{\pi}(s',a')] \end{align} $$
-
同时两个贝尔曼函数的关系也可由相关的回溯图表示出来
-
贝尔曼最优方程,一个直观解释:最优策略下某个状态的价值等于这个状态最有动作的期望汇报,从而有如下的状态价值函数和动作价值函数的最优方程: $$ v_{\star}=\max_{a}\sum_{s',r}p(s',r|s,a)[r+\gamma v_{\star}(s')]\ q_{\star}(s,a)=\sum_{s',r} p(s',r|s,a) [r+\gamma \max_{a'}q_{\star}(s',a')] $$
同时满足贝尔曼最优方程的策略一定是最优的策略,最优的策略一定满足最优方程