| layout |
title |
post |
Ensemble |
Un ensemble est une collection d'objets distincts. Ceci est loin d'être une définition rigoureuse, mais reflet bien l'intuition que tout le monde a des ensembles.
Toute la théorie des ensembles est basée sur la notion d'appartenance: on écrit $$a\in A$$ lorsque l'élément $$a$$ appartient à l'ensemble $$A$$. Toute propriété ou construction ensembliste peut être définie à partir de l'appartenance et de [connecteurs logiques](Logique mathématique).
L'accolade est le symbole de prédilection pour écrire un ensemble en notation mathématique. Par exemple, l'ensemble des voyelles de l'alphabet latin s'écrit $${a,e,i,o,u,y}$$. On parle de définition extensionnelle lorsque on écrit un ensemble en donnant la liste de ses éléments; bien évidemment ceci n'est possible que pour les ensembles finis.
Des ensembles infinis peuvent être construits par [définition inductive](Induction et récursion). Ceci s'applique, par exemple, aux [nombres naturels](Logique mathématique#système-de-péano).
De nouveaux ensembles peuvent être définis à partir d'ensembles plus grands en utilisant des [propositions logiques](Logique mathématique). Si $$A$$ est un ensemble et $$P$$ une proposition logique portant sur les éléments de $$A$$, on définit par compréhension l'ensemble $$B$$ des éléments de $$A$$ qui satisfont $$P$$. On note cela
$$B = {x\in A ;\vert; P(x)}.$$
Par exemple, on peut définir les nombres paires de la façon suivante:
$${x\in\mathbb{N} ;\vert; x = 0 \mod 2}.$$
Les diagrammes de Venn permettent de représenter graphiquement des propriétés logiques des ensembles. Un ensemble est représenté par un contour fermé contenant les éléments de l'ensemble à son intérieur. Un dessin explique mieux que cent mots, voici les diagrammes de Venn de trois ensembles: les alphabets latin, grec et cyrillique.
 {: width="300"}
{: width="300"}
On ne dessine pas nécessairement tous les élément d'un ensemble, par exemple quand il est infini.
On dit qu'un ensemble $$A$$ est contenu dans un ensemble $$B$$, et on écrit $$A\subset B$$, lorsque pour tout $$a\in A$$ on a aussi $$a\in B$$. En utilisant un [prédicat du premier ordre](Calcul des prédicats) on peut ré-écrire cela comme $$x\in A \Rightarrow x\in B.$$ Avec les diagrammes de Venn, l'inclusion ensembliste est naturellement exprimée par le dessin suivant.

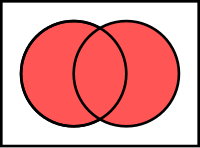
L'union de deux ensembles $$A$$ et $$B$$, notée $$A\cup B$$, est l'ensemble constitué de tous les éléments qui appartiennent soit à $$A$$, soit à $$B$$. En logique du premier ordre
$$x \in (A\cup B) \Leftrightarrow (x\in A \vee x\in B).$$
En diagrammes de Venn
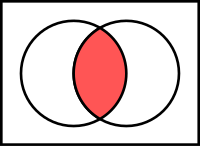
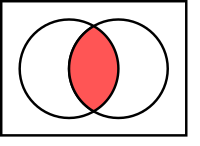
L'intersection de deux ensembles $$A$$ et $$B$$, notée $$A\cap B$$, est l'ensemble constitué de tous les éléments qui appartiennent à la fois à $$A$$ et à $$B$$. En logique du premier ordre
$$x \in (A\cap B) \Leftrightarrow (x\in A \wedge x\in B).$$
En diagrammes de Venn
Il est souvent sous-entendu que tous les ensembles ($$A$$, $$B$$, etc.) dont on parle sont contenus dans un ensemble plus grand, parfois appelé un univers et souvent noté $$U$$. Dans ce cas, on définit le complément d'un ensemble $$A$$ comme étant l'ensemble des $$x\in U$$ qui ne sont pas dans $$A$$, et on note $$\bar{A}$$. En logique du premier ordre
$$x\in\bar{A} \Leftrightarrow \neg x\in A.$$
En diagrammes de Venn (complément de l'ensemble de gauche)
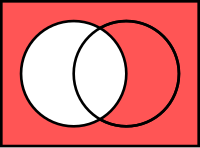
Le produit Cartésien de deux ensembles $$A$$ et $$B$$, noté $$A\times B$$, est l'ensemble formé de tous les couples $$(a,b)$$ avec $$a\in A$$ et $$b\in B$$. Le produit Cartésien n'est pas aisément exprimé en termes d'appartenance, par conséquent on est obligés d'introduire la notation de couple $$(\cdot,\cdot)$$ dans notre [langage](Calcul des prédicats#syntaxe):
$$(a,b)\in (A\times B) \Leftrightarrow a\in A \wedge b\in B.$$
On peut démontrer que le produit Cartésien est associatif, i.e. que
$$A\times(B\times C) = (A \times B) \times C,$$
par conséquent on note simplement $$A\times B \times C$$ ce produit. Le produit Cartesien $$A\times A$$ est aussi noté $$A^2$$, et $$A^n$$ représente le produit $$A\times\cdots\times A$$ de $$n$$ copies de $$A$$.
Exercice : Prouvez l'associativité du produit Cartésien.
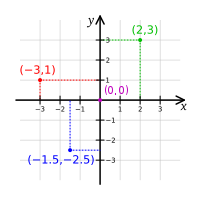
Le produit Cartésien ne se prête pas bien à la représentation par diagrammes de Venn. On peut quand même le représenter dans un plan (ou en espace à plusieurs dimensions, dans le cas d'un produit de plusieurs ensembles) en identifiant les axes des abscisses et des ordonnées aux éléments de $$A$$ et de $$B$$ et en identifiant les points du plan aux couples $$(a,b)$$. Voici la représentation du produit Cartésien de deux copies des nombres réels $$\mathbb{R}^2$$ (il s'agit du plan Cartésien bien connu en analyse).
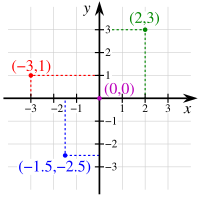
Voir aussi le graphe d'une fonction.
La différence ensembliste de $$A$$ par $$B$$, notéé $$A\backslash B$$, est définie par la formule
$$x\in(A\backslash B) \Leftrightarrow (x\in A \wedge \neg x\in B).$$
La différence symétrique de $$A$$ et $$B$$, notéé $$A,\Delta, B$$, est définie par la formule
$$x\in(A,\Delta, B) \Leftrightarrow (x\in A\backslash B \vee x\in B\backslash A).$$
Exercice: Dessinez les diagrammes de Venn des différences ensembliste et symétrique.
Étant donné un ensemble $$A$$, on note $$\mathcal{P}(A)$$ son ensemble des parties, c'est à dire l'ensemble contenant tous les sous-ensembles de $$A$$. Les diagrammes de Venn ne peuvent pas représenter l'ensemble des parties de façon convenable.
Exercice: Donnez une formule logique du premier ordre exprimant "$$B$$ est l'ensemble des parties de $$A$$". Donnez-en une version qui n'utilise que le symbole d'appartenance et des connecteurs logiques du premier ordre.
Voir Fonction.
Une fonction d'un ensemble $$A$$ vers un ensemble $$B$$ est une loi qui associe à chaque élément de $$A$$ un unique élément de $$B$$.

Voir Cardinalité
La cardinalité d'un ensemble $$A$$, notée $$|A|$$ ou $$#A$$, est le
nombre d'éléments de $$A$$. Si $$A$$ est infini, sa cardinalité est
infinie, il existent cependant
plusieurs sortes d'infini.
Exercice: Montrer par [induction](Induction et récursion) que deux ensembles
finis $$A$$ et $$B$$ peuvent être mis en
bijection si et seulement si $$|A|=|B|$$.
Voici une liste de quelques ensembles bien connus.
- L'ensemble vide, noté $$\emptyset$$, qui ne contient aucun élément et qui a cardinalité 0.
- L'alphabet latin est un ensemble fini de cardinalité 26;
- Les nombres naturels $$\mathbb{N}$$, $${0, 1, 2, \ldots}$$;
- Les entiers $$\mathbb{Z}$$, $${\ldots, -2, -1, 0, 1, 2, \ldots}$$;
- Les rationnels $$\mathbb{Q}$$, c'est à dire les nombres qui peuvent être écrits sous forme de fraction $$\frac{a}{b}$$ avec $$a,b\in\mathbb{Z}$$;
- Les réels $$\mathbb{R}$$, c'est à dire les nombres qui peuvent être écrit comme la limite d'une suite de rationnels;
- Les complexes $$\mathbb{C}$$, c'est à dire les nombres de la forme $$a+ib$$ avec $$a,b\in\mathbb{R}$$ et $$i=\sqrt{-1}$$;
- Pour tout alphabet $$\Sigma$$ (non nécessairement fini), on note $$\Sigma^\ast$$ l'ensemble de toutes less chaînes de caractères sur l'alphabet.
Il n'existe pas de chose tel l'ensemble de tous les ensembles. Russel a montré que supposer son existence entraîne une contraddiction. Voir cette page Wikipedia.