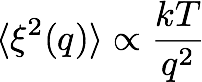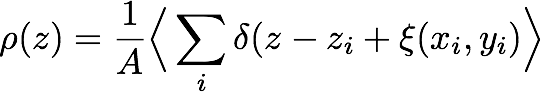How does the presence of an interface between two fluids change their properties? All observables should in principle depend on the distance from the interface, but the presence of capillary waves induced by thermal fluctuations complicates their calculation, as the wave modes spectrum depends on the wave vector q as
and the larger your sample is, the larger will be the amplitude of compatible, long wavelength excitations. These capillary waves will smear any profile that is computed across the interface. If the position of the interface is in contrary known at each and every point, it is possible to construct profiles ρ(z) which are intrinsic (with respect to the interface),
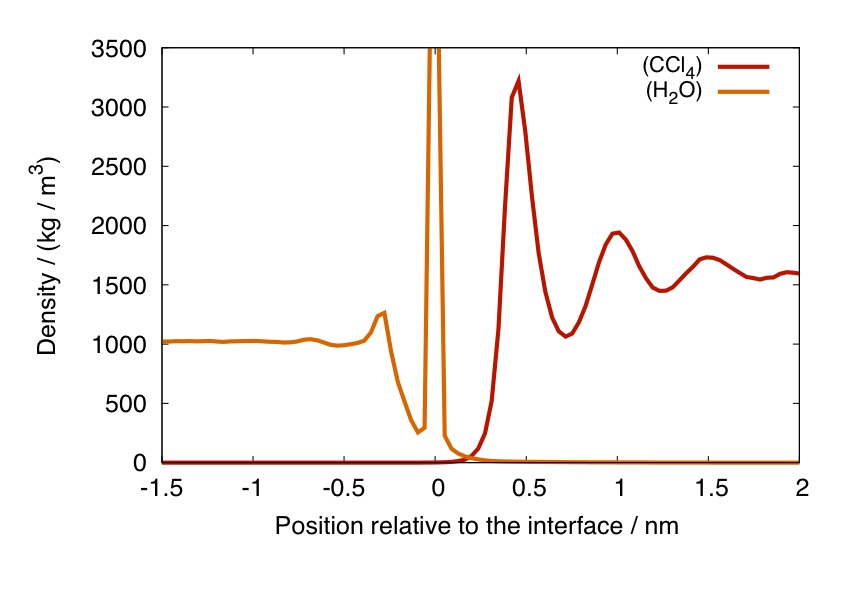
where the index i identifies the i-th particle in one phase, and z is now the position with respect to the local interface. The usual, smoothed, density profiles, once computed with respect to the local interface position, start showing rich features like in the case presented in the plot below, showing the intrinsic mass density profile at the water / carbon tetrachloride interface.
Intrinsic mass density profile of water (left) and carbon tetrachloride at the interface between the two fluids, with respect to the water phase.
This profile has been calculated using the water phase to define the interface. For this reason, at zero intrinsic distance (i.e., at the surface) there will be only atoms from the water phase, hence, the Dirac delta contribution at z=0.