README.md

1057. 校园自行车分配

English Version

题目描述

在 X-Y 平面上表示的校园中，有 n 名工人和 m 辆自行车，其中 n <= m。

给定一个长度为 n 的数组 workers ，其中 worker [i] = [xi, yi] 表示第 i 个工人的位置。你也得到一个长度为 m 的自行车数组 bikers ，其中 bikes[j] = [xj, yj] 是第 j 辆自行车的位置。所有给定的位置都是 唯一 的。

我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中，我们选取彼此之间 曼哈顿距离 最短的工人自行车对 (workeri, bikej) ，并将其中的自行车分配給工人。

如果有多个 (workeri, bikej) 对之间的 曼哈顿距离 相同，那么我们选择 工人索引最小 的那对。类似地，如果有多种不同的分配方法，则选择 自行车索引最小 的一对。不断重复这一过程，直到所有工人都分配到自行车为止。

返回长度为 n 的向量 answer，其中 answer[i] 是第 i 位工人分配到的自行车的索引（从 0 开始）。

给定两点 p1 和 p2 之间的 曼哈顿距离 为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。

 

示例 1：

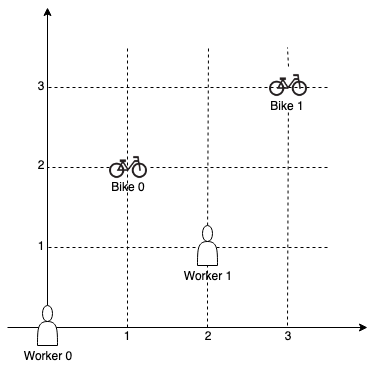
输入：workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
输出：[1,0]
解释：工人 1 分配到自行车 0，因为他们最接近且不存在冲突，工人 0 分配到自行车 1 。所以输出是 [1,0]。

示例 2：

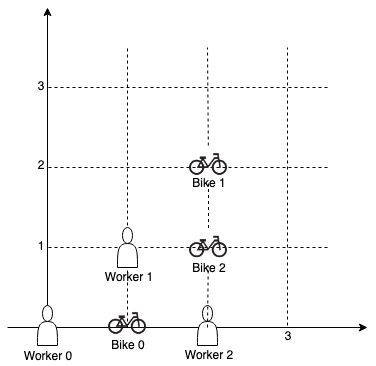
输入：workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
输出：[0,2,1]
解释：工人 0 首先分配到自行车 0 。工人 1 和工人 2 与自行车 2 距离相同，因此工人 1 分配到自行车 2，工人 2 将分配到自行车 1 。因此输出为 [0,2,1]。

 

提示：

• n == workers.length
• m == bikes.length
• 1 <= n <= m <= 1000
• workers[i].length == bikes[j].length == 2
• 0 <= xi, yi < 1000
• 0 <= xj, yj < 1000
• 所有工人和自行车的位置都不相同

解法

方法一：排序

先计算每个工人和每个自行车之间的曼哈顿距离，然后按照曼哈顿距离从小到大排序，遍历排序后的数组，如果当前工人和自行车都未被分配，则分配给当前工人和自行车。

时间复杂度 $O(n\times m\times \log (n\times m))$。其中 $n$ 和 $m$ 分别为工人和自行车的数量。

Python3

class Solution:
    def assignBikes(self, workers: List[List[int]], bikes: List[List[int]]) -> List[int]:
        n, m = len(workers), len(bikes)
        arr = []
        for i, j in product(range(n), range(m)):
            dist = abs(workers[i][0] - bikes[j][0]) + \
                abs(workers[i][1] - bikes[j][1])
            arr.append((dist, i, j))
        arr.sort()
        vis1 = [False] * n
        vis2 = [False] * m
        ans = [0] * n
        for _, i, j in arr:
            if not vis1[i] and not vis2[j]:
                vis1[i] = vis2[j] = True
                ans[i] = j
        return ans

Java

class Solution {
    public int[] assignBikes(int[][] workers, int[][] bikes) {
        int n = workers.length, m = bikes.length;
        int[][] arr = new int[m * n][3];
        for (int i = 0, k = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int dist
                    = Math.abs(workers[i][0] - bikes[j][0]) + Math.abs(workers[i][1] - bikes[j][1]);
                arr[k++] = new int[] {dist, i, j};
            }
        }
        Arrays.sort(arr, (a, b) -> {
            if (a[0] != b[0]) {
                return a[0] - b[0];
            }
            if (a[1] != b[1]) {
                return a[1] - b[1];
            }
            return a[2] - b[2];
        });
        boolean[] vis1 = new boolean[n];
        boolean[] vis2 = new boolean[m];
        int[] ans = new int[n];
        for (var e : arr) {
            int i = e[1], j = e[2];
            if (!vis1[i] && !vis2[j]) {
                vis1[i] = true;
                vis2[j] = true;
                ans[i] = j;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        int n = workers.size(), m = bikes.size();
        vector<tuple<int, int, int>> arr(n * m);
        for (int i = 0, k = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int dist = abs(workers[i][0] - bikes[j][0]) + abs(workers[i][1] - bikes[j][1]);
                arr[k++] = {dist, i, j};
            }
        }
        sort(arr.begin(), arr.end());
        vector<bool> vis1(n), vis2(m);
        vector<int> ans(n);
        for (auto& [_, i, j] : arr) {
            if (!vis1[i] && !vis2[j]) {
                vis1[i] = true;
                vis2[j] = true;
                ans[i] = j;
            }
        }
        return ans;
    }
};

Go

func assignBikes(workers [][]int, bikes [][]int) []int {
	n, m := len(workers), len(bikes)
	type tuple struct{ d, i, j int }
	arr := make([]tuple, n*m)
	for i, k := 0, 0; i < n; i++ {
		for j := 0; j < m; j++ {
			d := abs(workers[i][0]-bikes[j][0]) + abs(workers[i][1]-bikes[j][1])
			arr[k] = tuple{d, i, j}
			k++
		}
	}
	sort.Slice(arr, func(i, j int) bool {
		if arr[i].d != arr[j].d {
			return arr[i].d < arr[j].d
		}
		if arr[i].i != arr[j].i {
			return arr[i].i < arr[j].i
		}
		return arr[i].j < arr[j].j
	})
	vis1, vis2 := make([]bool, n), make([]bool, m)
	ans := make([]int, n)
	for _, e := range arr {
		i, j := e.i, e.j
		if !vis1[i] && !vis2[j] {
			vis1[i], vis2[j] = true, true
			ans[i] = j
		}
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

...