Skip to content

Latest commit

 

History

History
227 lines (188 loc) · 6.77 KB

README.md

File metadata and controls

227 lines (188 loc) · 6.77 KB
Raw

1782. 统计点对的数目

English Version

题目描述

给你一个无向图，无向图由整数 n  ，表示图中节点的数目，和 edges 组成，其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。

第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目：

  • a < b
  • cnt 是与 a 或者 b 相连的边的数目，且 cnt 严格大于 queries[j] 。

请你返回一个数组 answers ，其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。

请注意，图中可能会有 重复边 。

 

示例 1：

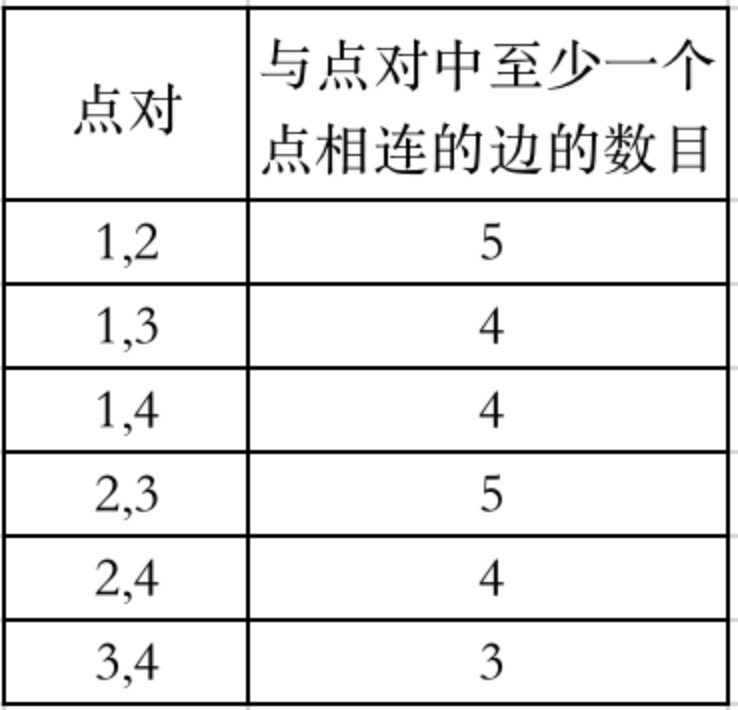
输入：n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出：[6,5]
解释：每个点对中，与至少一个点相连的边的数目如上图所示。

示例 2：

输入：n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出：[10,10,9,8,6]

 

提示：

  • 2 <= n <= 2 * 104
  • 1 <= edges.length <= 105
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= queries.length <= 20
  • 0 <= queries[j] < edges.length

解法

方法一：哈希表 + 排序 + 二分查找

根据题目，我们可以知道，与点对 $(a, b)$ 相连的边数等于“与 $a$ 相连的边数”加上“与 $b$ 相连的边数”，再减去同时与 $a$ 和 $b$ 相连的边数。

因此，我们可以先用数组 $cnt$ 统计与每个点相连的边数，用哈希表 $g$ 统计每个点对的数量。

然后，对于每个查询 $q$，我们可以枚举 $a$，对于每个 $a$，我们可以通过二分查找找到第一个满足 $cnt[a] + cnt[b] &gt; q$ 的 $b$，先将数量累加到 $ans$ 中，再减去一部分重复的边数。

时间复杂度 $O(m\times n\times \log n)$。

Python3

class Solution:
    def countPairs(self, n: int, edges: List[List[int]], queries: List[int]) -> List[int]:
        cnt = [0] * n
        g = defaultdict(int)
        for a, b in edges:
            a, b = a - 1, b - 1
            cnt[a] += 1
            cnt[b] += 1
            if a > b:
                a, b = b, a
            g[(a, b)] += 1

        s = sorted(cnt)
        ans = [0] * len(queries)
        for i, t in enumerate(queries):
            for j, x in enumerate(s):
                k = bisect_right(s, t - x, lo=j+1)
                ans[i] += n - k
            for (a, b), v in g.items():
                if cnt[a] + cnt[b] > t and cnt[a] + cnt[b] - v <= t:
                    ans[i] -= 1
        return ans

Java

class Solution {
    public int[] countPairs(int n, int[][] edges, int[] queries) {
        int[] cnt = new int[n];
        Map<Integer, Integer> g = new HashMap<>();
        for (var e : edges) {
            int a = e[0] - 1, b = e[1] - 1;
            ++cnt[a];
            ++cnt[b];
            int k = Math.min(a, b) * n + Math.max(a, b);
            g.put(k, g.getOrDefault(k, 0) + 1);
        }
        int[] s = cnt.clone();
        Arrays.sort(s);
        int[] ans = new int[queries.length];
        for (int i = 0; i < queries.length; ++i) {
            int t = queries[i];
            for (int j = 0; j < n; ++j) {
                int x = s[j];
                int k = search(s, t - x, j + 1);
                ans[i] += n - k;
            }
            for (var e : g.entrySet()) {
                int a = e.getKey() / n, b = e.getKey() % n;
                int v = e.getValue();
                if (cnt[a] + cnt[b] > t && cnt[a] + cnt[b] - v <= t) {
                    --ans[i];
                }
            }
        }
        return ans;
    }

    private int search(int[] arr, int x, int i) {
        int left = i, right = arr.length;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (arr[mid] > x) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

C++

class Solution {
public:
    vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {
        vector<int> cnt(n);
        unordered_map<int, int> g;
        for (auto& e : edges) {
            int a = e[0] - 1, b = e[1] - 1;
            ++cnt[a];
            ++cnt[b];
            int k = min(a, b) * n + max(a, b);
            ++g[k];
        }
        vector<int> s = cnt;
        sort(s.begin(), s.end());
        vector<int> ans(queries.size());
        for (int i = 0; i < queries.size(); ++i) {
            int t = queries[i];
            for (int j = 0; j < n; ++j) {
                int x = s[j];
                int k = upper_bound(s.begin() + j + 1, s.end(), t - x) - s.begin();
                ans[i] += n - k;
            }
            for (auto& [k, v] : g) {
                int a = k / n, b = k % n;
                if (cnt[a] + cnt[b] > t && cnt[a] + cnt[b] - v <= t) {
                    --ans[i];
                }
            }
        }
        return ans;
    }
};

Go

func countPairs(n int, edges [][]int, queries []int) []int {
	cnt := make([]int, n)
	g := map[int]int{}
	for _, e := range edges {
		a, b := e[0]-1, e[1]-1
		cnt[a]++
		cnt[b]++
		if a > b {
			a, b = b, a
		}
		g[a*n+b]++
	}
	s := make([]int, n)
	copy(s, cnt)
	sort.Ints(s)
	ans := make([]int, len(queries))
	for i, t := range queries {
		for j, x := range s {
			k := sort.Search(n, func(h int) bool { return s[h] > t-x && h > j })
			ans[i] += n - k
		}
		for k, v := range g {
			a, b := k/n, k%n
			if cnt[a]+cnt[b] > t && cnt[a]+cnt[b]-v <= t {
				ans[i]--
			}
		}
	}
	return ans
}

...