README.md

2212. 射箭比赛中的最大得分

English Version

题目描述

Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下：

1. Alice 先射 numArrows 支箭，然后 Bob 也射 numArrows 支箭。
2. 分数按下述规则计算：
   1. 箭靶有若干整数计分区域，范围从 0 到 11 （含 0 和 11）。
   2. 箭靶上每个区域都对应一个得分 k（范围是 0 到 11），Alice 和 Bob 分别在得分 k 区域射中 ak 和 bk 支箭。如果 ak >= bk ，那么 Alice 得 k 分。如果 ak < bk ，则 Bob 得 k 分
   3. 如果 ak == bk == 0 ，那么无人得到 k 分。

• 例如，Alice 和 Bob 都向计分为 11 的区域射 2 支箭，那么 Alice 得 11 分。如果 Alice 向计分为 11 的区域射 0 支箭，但 Bob 向同一个区域射 2 支箭，那么 Bob 得 11 分。

给你整数 numArrows 和一个长度为 12 的整数数组 aliceArrows ，该数组表示 Alice 射中 0 到 11 每个计分区域的箭数量。现在，Bob 想要尽可能 最大化 他所能获得的总分。

返回数组 bobArrows ，该数组表示 Bob 射中 0 到 11 每个 计分区域的箭数量。且 bobArrows 的总和应当等于 numArrows 。

如果存在多种方法都可以使 Bob 获得最大总分，返回其中 任意一种 即可。

 

示例 1：

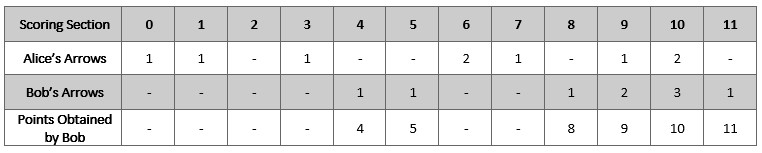
输入：numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
输出：[0,0,0,0,1,1,0,0,1,2,3,1]
解释：上表显示了比赛得分情况。
Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。
可以证明 Bob 无法获得比 47 更高的分数。

示例 2：

输入：numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
输出：[0,0,0,0,0,0,0,0,1,1,1,0]
解释：上表显示了比赛得分情况。
Bob 获得总分 8 + 9 + 10 = 27 。
可以证明 Bob 无法获得比 27 更高的分数。

 

提示：

• 1 <= numArrows <= 105
• aliceArrows.length == bobArrows.length == 12
• 0 <= aliceArrows[i], bobArrows[i] <= numArrows
• sum(aliceArrows[i]) == numArrows

解法

方法一：二进制枚举

枚举 bob 射箭的最终状态，寻找满足题意的、且使得 bob 得分最大的状态。

Python3

class Solution:
    def maximumBobPoints(self, numArrows: int, aliceArrows: List[int]) -> List[int]:
        n = len(aliceArrows)
        state = 0
        mx = -1
        for mask in range(1 << n):
            cnt = points = 0
            for i, alice in enumerate(aliceArrows):
                if (mask >> i) & 1:
                    cnt += alice + 1
                    points += i
            if cnt <= numArrows and mx < points:
                state = mask
                mx = points
        ans = [0] * n
        for i, alice in enumerate(aliceArrows):
            if (state >> i) & 1:
                ans[i] = alice + 1
                numArrows -= ans[i]
        ans[0] = numArrows
        return ans

Java

class Solution {
    public int[] maximumBobPoints(int numArrows, int[] aliceArrows) {
        int n = aliceArrows.length;
        int mx = -1;
        int state = 0;
        for (int mask = 1; mask < 1 << n; ++mask) {
            int cnt = 0, points = 0;
            for (int i = 0; i < n; ++i) {
                if (((mask >> i) & 1) == 1) {
                    cnt += aliceArrows[i] + 1;
                    points += i;
                }
            }
            if (cnt <= numArrows && mx < points) {
                state = mask;
                mx = points;
            }
        }
        int[] ans = new int[n];
        for (int i = 0; i < n; ++i) {
            if (((state >> i) & 1) == 1) {
                ans[i] = aliceArrows[i] + 1;
                numArrows -= ans[i];
            }
        }
        ans[0] += numArrows;
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> maximumBobPoints(int numArrows, vector<int>& aliceArrows) {
        int n = aliceArrows.size();
        int state = 0, mx = -1;
        for (int mask = 1; mask < 1 << n; ++mask) {
            int cnt = 0, points = 0;
            for (int i = 0; i < n; ++i) {
                if ((mask >> i) & 1) {
                    cnt += aliceArrows[i] + 1;
                    points += i;
                }
            }
            if (cnt <= numArrows && mx < points) {
                state = mask;
                mx = points;
            }
        }
        vector<int> ans(n);
        for (int i = 0; i < n; ++i) {
            if ((state >> i) & 1) {
                ans[i] = aliceArrows[i] + 1;
                numArrows -= ans[i];
            }
        }
        ans[0] += numArrows;
        return ans;
    }
};

Go

func maximumBobPoints(numArrows int, aliceArrows []int) []int {
	n := len(aliceArrows)
	state, mx := 0, -1
	for mask := 1; mask < 1<<n; mask++ {
		cnt, points := 0, 0
		for i, alice := range aliceArrows {
			if (mask>>i)&1 == 1 {
				cnt += alice + 1
				points += i
			}
		}
		if cnt <= numArrows && mx < points {
			state = mask
			mx = points
		}
	}
	ans := make([]int, n)
	for i, alice := range aliceArrows {
		if (state>>i)&1 == 1 {
			ans[i] = alice + 1
			numArrows -= ans[i]
		}
	}
	ans[0] += numArrows
	return ans
}

TypeScript

function maximumBobPoints(numArrows: number, aliceArrows: number[]): number[] {
    const dfs = (arr: number[], i: number, c: number): number[] => {
        if (i < 0 || c === 0) {
            arr[0] += c;
            return arr;
        }
        const a1 = dfs([...arr], i - 1, c);
        if (c > aliceArrows[i]) {
            arr[i] = aliceArrows[i] + 1;
            const a2 = dfs(arr, i - 1, c - aliceArrows[i] - 1);
            if (
                a2.reduce((p, v, i) => p + (v > 0 ? i : 0), 0) >=
                a1.reduce((p, v, i) => p + (v > 0 ? i : 0), 0)
            ) {
                return a2;
            }
        }
        return a1;
    };
    return dfs(new Array(12).fill(0), 11, numArrows);
}

Rust

impl Solution {
    fn dfs(alice_arrows: &Vec<i32>, mut res: Vec<i32>, count: i32, i: usize) -> Vec<i32> {
        if i == 0 || count == 0 {
            res[0] += count;
            return res;
        }
        let r1 = Self::dfs(alice_arrows, res.clone(), count, i - 1);
        if count > alice_arrows[i] {
            res[i] = alice_arrows[i] + 1;
            let r2 = Self::dfs(alice_arrows, res, count - alice_arrows[i] - 1, i - 1);
            if r2
                .iter()
                .enumerate()
                .map(|(i, v)| if v > &0 { i } else { 0 })
                .sum::<usize>()
                > r1.iter()
                    .enumerate()
                    .map(|(i, v)| if v > &0 { i } else { 0 })
                    .sum::<usize>()
            {
                return r2;
            }
        }
        r1
    }

    pub fn maximum_bob_points(num_arrows: i32, alice_arrows: Vec<i32>) -> Vec<i32> {
        Self::dfs(&alice_arrows, vec![0; 12], num_arrows, 11)
    }
}

...