README.md

2328. 网格图中递增路径的数目

English Version

题目描述

给你一个 m x n 的整数网格图 grid ，你可以从一个格子移动到 4 个方向相邻的任意一个格子。

请你返回在网格图中从 任意 格子出发，达到 任意 格子，且路径中的数字是 严格递增 的路径数目。由于答案可能会很大，请将结果对 109 + 7 取余 后返回。

如果两条路径中访问过的格子不是完全相同的，那么它们视为两条不同的路径。

 

示例 1：

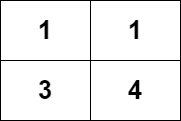
输入：grid = [[1,1],[3,4]]
输出：8
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[1]，[3]，[4] 。
- 长度为 2 的路径：[1 -> 3]，[1 -> 4]，[3 -> 4] 。
- 长度为 3 的路径：[1 -> 3 -> 4] 。
路径数目为 4 + 3 + 1 = 8 。

示例 2：

输入：grid = [[1],[2]]
输出：3
解释：严格递增路径包括：
- 长度为 1 的路径：[1]，[2] 。
- 长度为 2 的路径：[1 -> 2] 。
路径数目为 2 + 1 = 3 。

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 105

解法

方法一：记忆化搜索

时间复杂度 $O(mn)$。

相似题目：329. 矩阵中的最长递增路径。

Python3

class Solution:
    def countPaths(self, grid: List[List[int]]) -> int:
        @cache
        def dfs(i, j):
            res = 1
            for a, b in [[0, -1], [0, 1], [-1, 0], [1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y] > grid[i][j]:
                    res += dfs(x, y)
            return res

        m, n = len(grid), len(grid[0])
        mod = 10**9 + 7
        return sum(dfs(i, j) for i in range(m) for j in range(n)) % mod

Java

class Solution {
    private int m;
    private int n;
    private int[][] g;
    private int[][] f;
    private static final int MOD = (int) 1e9 + 7;

    public int countPaths(int[][] grid) {
        g = grid;
        m = g.length;
        n = g[0].length;
        f = new int[m][n];
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                ans = (ans + dfs(i, j)) % MOD;
            }
        }
        return ans;
    }

    private int dfs(int i, int j) {
        if (f[i][j] != 0) {
            return f[i][j];
        }
        int res = 1;
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && g[x][y] > g[i][j]) {
                res = (res + dfs(x, y)) % MOD;
            }
        }
        f[i][j] = res;
        return res;
    }
}

C++

class Solution {
public:
    const int mod = 1e9 + 7;
    int countPaths(vector<vector<int>>& grid) {
        int ans = 0;
        vector<vector<int>> f(grid.size(), vector<int>(grid[0].size()));
        for (int i = 0; i < grid.size(); ++i)
            for (int j = 0; j < grid[0].size(); ++j)
                ans = (ans + dfs(i, j, f, grid)) % mod;
        return ans;
    }

    int dfs(int i, int j, vector<vector<int>>& f, vector<vector<int>>& g) {
        if (f[i][j]) return f[i][j];
        int res = 1;
        vector<int> dirs = {-1, 0, 1, 0, -1};
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < g.size() && y >= 0 && y < g[0].size() && g[x][y] > g[i][j])
                res = (res + dfs(x, y, f, g)) % mod;
        }
        f[i][j] = res;
        return res;
    }
};

Go

func countPaths(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	f := make([][]int, m)
	for i := range f {
		f[i] = make([]int, n)
	}
	mod := int(1e9) + 7
	ans := 0
	dirs := []int{-1, 0, 1, 0, -1}
	var dfs func(int, int) int
	dfs = func(i, j int) int {
		if f[i][j] > 0 {
			return f[i][j]
		}
		res := 1
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > grid[i][j] {
				res = (res + dfs(x, y)) % mod
			}
		}
		f[i][j] = res
		return res
	}
	for i, row := range grid {
		for j := range row {
			ans = (ans + dfs(i, j)) % mod
		}
	}
	return ans
}

TypeScript

function countPaths(grid: number[][]): number {
    const mod = BigInt(10 ** 9 + 7);
    const dirs = [
        [0, 1],
        [1, 0],
        [0, -1],
        [-1, 0],
    ];
    const m = grid.length,
        n = grid[0].length;
    const dp = Array.from({ length: m }, v => new Array(n).fill(-1n));

    function dfs(x, y) {
        if (dp[x][y] != -1) return dp[x][y];
        let count = 1n;
        for (let [dx, dy] of dirs) {
            let i = x + dx,
                j = y + dy;
            if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] <= grid[x][y])
                continue;
            count = (count + dfs(i, j)) % mod;
        }
        dp[x][y] = count;
        return count;
    }

    let sum = 0n;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            sum = (sum + dfs(i, j)) % mod;
        }
    }
    return Number(sum);
}

...