The DFS algorithm is a recursive algorithm that uses the idea of backtracking. It involves exhaustive searches of all the nodes by going ahead, if possible, else by backtracking.
Let us understand this algorithm with a example.
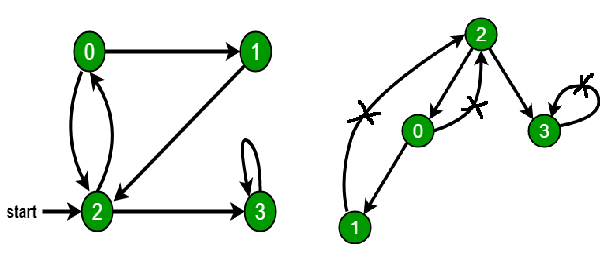
1.For example, in the following graph, we start traversal from vertex 2. 2.When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. 3. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. 4.A Depth First Traversal of the following graph is 2, 0, 1, 3.
- Pick a starting node and push all its adjacent nodes into a stack.
- Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
- Repeat this process until the stack is empty.
- However, ensure that the nodes that are visited are marked. This will prevent you from visiting the same node more than once. If you do not mark the nodes that are visited and you visit the same node more than once, you may end up in an infinite loop.
The pseudocode for Depth First Search algorithm is as follows:
Procedure depth_first_search
DFS-iterative (G, s): //Where G is graph and s is source vertex
let S be stack
S.push( s ) //Inserting s in stack
mark s as visited.
while ( S is not empty):
//Pop a vertex from stack to visit next
v = S.top( )
S.pop( )
//Push all the neighbour
**Time complexity** - s of v in stack that are not visited
for all neighbours w of v in Graph G:
if w is not visited :
S.push( w )
mark w as visited
DFS-recursive(G, s):
mark s as visited
for all neighbours w of s in Graph G:
if w is not visited:
DFS-recursive(G, w)
end procedure
Time complexity - O(V+E), where V and E are number of vertices and edges.