-
Notifications
You must be signed in to change notification settings - Fork 36
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
[BUG] Geometric Curve-Curve Intersection breaks down when linearized segments are vastly different in size #234
Comments
|
It's definitely giving the wrong answer, I'm not sure if it's a true "bug" or if it's a problem with robustness against round-off and all real inputs. I have computed the exact answer as follows: Create the
|
|
I've learned a bit more; after 12 refinements the candidate segments from both I think the primary issue is that the size of This may necessitate a change in the way geometric intersection is done. The current approach (I'm working on documenting it here https://bezier.readthedocs.io/en/latest/algorithms/geometric-curve-intersection.html) is to stop subdividing once one of the curves becomes linear. However, the massive difference in scale (4096 difference in the parameter range) may be causing issues here. |
|
Based on https://doi.org/10.1016/j.cagd.2019.101791 / https://github.com/dhermes/condition-number-bezier-curve-intersection, I calculated the 2-norm condition number of the intersection to be |
|
The issue happens here when trying to intersect In [25]: first, second
Out[25]:
(<bezier.hazmat.geometric_intersection.Linearization at 0x7fce42071880>,
<bezier.hazmat.geometric_intersection.Linearization at 0x7fce421cc640>)
In [26]: first.start_node
Out[26]: array([ 2.88885635, 10.70018271])
In [27]: first.end_node
Out[27]: array([-1.50807125, -8.81050738])
In [28]: second.start_node
Out[28]: array([0.49975586, 0.09999998])
In [29]: second.end_node
Out[29]: array([0.5, 0.1])
In [30]: s, t, success = segment_intersection(
...: first.start_node, first.end_node, second.start_node, second.end_node
...: )
In [31]: s, t, success
Out[31]: (0.5433012701892219, 1.0000000000009721, True)
In [32]: _py_helpers.in_interval(s, 0.0, 1.0)
Out[32]: True
In [33]: _py_helpers.in_interval(t, 0.0, 1.0)
Out[33]: False |
|
Thank you very much for investigating my problem. If it is a robustness problem, how should we handle this case? To give a small random perturbation to the endpoints of the line? |
That could work. Another thing that could work would be to manually do the work of bisection by replacing the line with multiple sub-segments of it via |
|
Just a single subdivision does the trick (though this is still not something you should have to resort to): In [1]: import bezier
In [2]: import numpy as np
In [3]: nodes1 = np.asfortranarray(
...: [
...: [2.8888563469481592, -1.5080712474161317],
...: [10.700182708846356, -8.8105073796645534],
...: ]
...: )
In [4]: nodes2 = np.asfortranarray([[0.0, 0.5, 1.0], [0.0, 0.20000000298023224, 0.0]])
In [5]: curve1 = bezier.Curve.from_nodes(nodes1)
In [6]: curve2 = bezier.Curve.from_nodes(nodes2)
In [7]: curve1.intersect(curve2)
Out[7]: array([], shape=(2, 0), dtype=float64)
In [8]: curve1a, curve1b = curve1.subdivide()
In [9]: curve1a.intersect(curve2)
Out[9]: array([], shape=(2, 0), dtype=float64)
In [10]: intersections_b = curve1b.intersect(curve2)
In [11]: intersections_b
Out[11]:
array([[0.08660254],
[0.5 ]])
In [12]: s_val = 0.5 + 0.5 * intersections_b[0, 0]
In [13]: t_val = intersections_b[1, 0]
In [14]: curve1.evaluate(s_val)
Out[14]:
array([[0.5],
[0.1]])
In [15]: curve2.evaluate(t_val)
Out[15]:
array([[0.5],
[0.1]])
In [16]: s_val
Out[16]: 0.5433012701892219Also note that |
Hi,
I found a bug when using this library.
The code return empty list [] but the actual intersection should be as following:
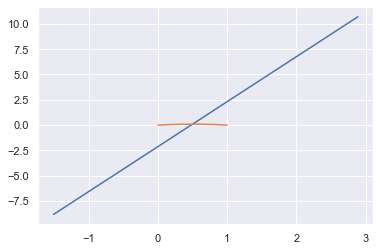
Do I miss to set up some parameters?
Best
Ziqi Wang
The text was updated successfully, but these errors were encountered: