README.md

391. Perfect Rectangle

Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).

Return true if all the rectangles together form an exact cover of a rectangular region.

Example 1:

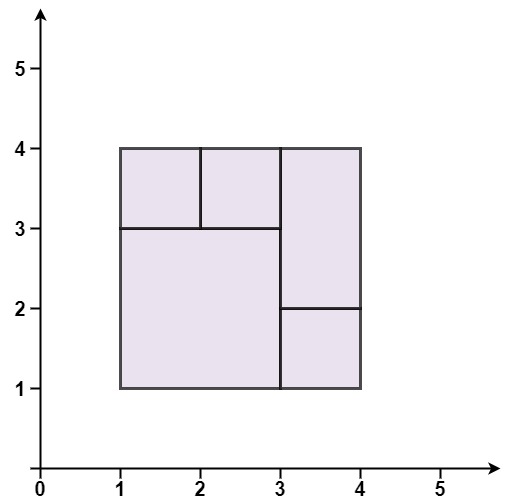
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.

Example 2:

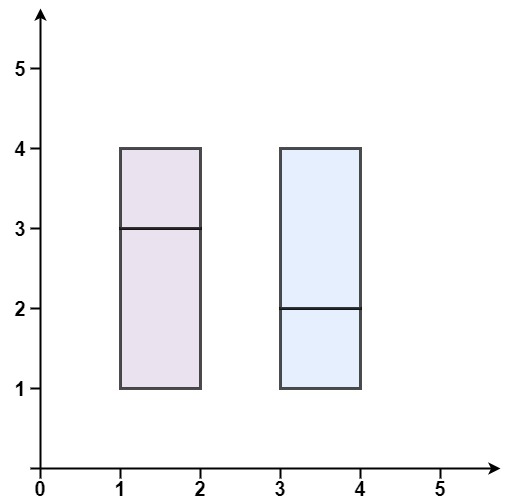
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.

Example 3:

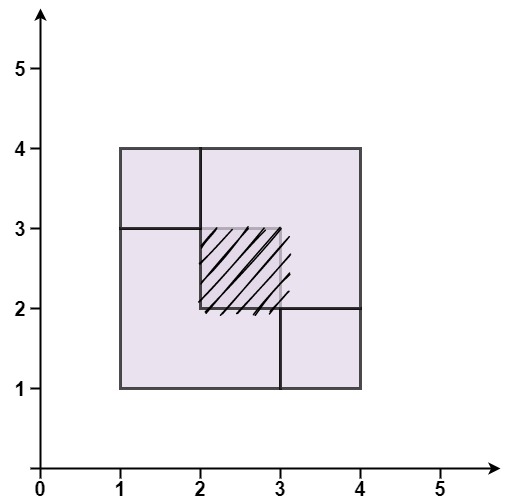
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.

Constraints:

• 1 <= rectangles.length <= 2 * 104
• rectangles[i].length == 4
• -105 <= xi, yi, ai, bi <= 105

Solutions (Rust)

1. Solution

use std::collections::HashMap;

impl Solution {
    pub fn is_rectangle_cover(rectangles: Vec<Vec<i32>>) -> bool {
        let (mut minx, mut miny, mut maxa, mut maxb) = (i32::MAX, i32::MAX, i32::MIN, i32::MIN);
        let mut area = 0;
        let mut count = HashMap::new();

        for rect in &rectangles {
            let (x, y, a, b) = (rect[0], rect[1], rect[2], rect[3]);
            minx = minx.min(x);
            miny = miny.min(y);
            maxa = maxa.max(a);
            maxb = maxb.max(b);
            area += (a - x) as i64 * (b - y) as i64;
            *count.entry((x, y)).or_insert(0) += 1;
            *count.entry((x, b)).or_insert(0) += 1;
            *count.entry((a, y)).or_insert(0) += 1;
            *count.entry((a, b)).or_insert(0) += 1;
        }

        if (maxa - minx) as i64 * (maxb - miny) as i64 != area {
            return false;
        }

        for (&(x, y), &c) in count.iter() {
            if (x == minx || x == maxa) && (y == miny || y == maxb) && c != 1 {
                return false;
            } else if ((x != minx && x != maxa) || (y != miny && y != maxb)) && c != 2 && c != 4 {
                return false;
            }
        }

        true
    }
}