README.md

587. Erect the Fence

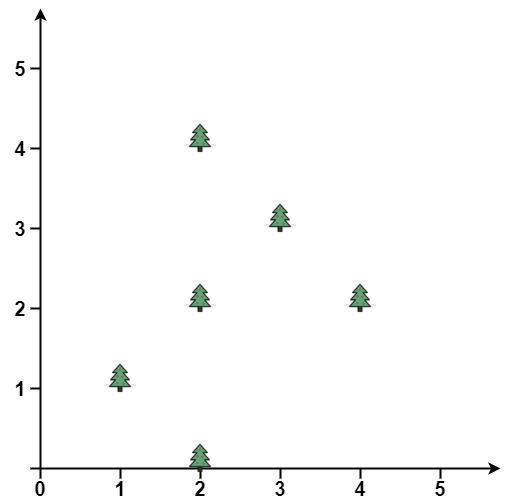
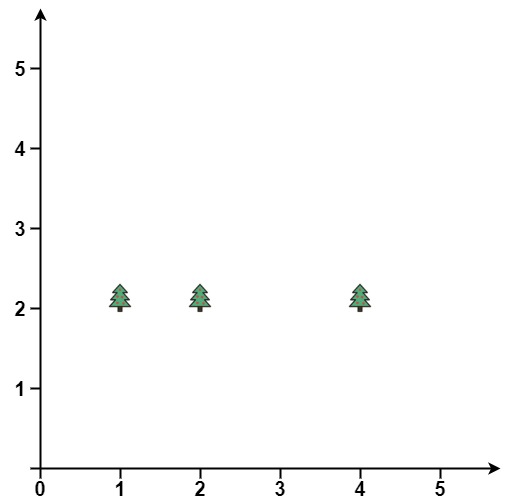
You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.

Fence the entire garden using the minimum length of rope, as it is expensive. The garden is well-fenced only if all the trees are enclosed.

Return the coordinates of trees that are exactly located on the fence perimeter. You may return the answer in any order.

Example 1:

Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation: All the trees will be on the perimeter of the fence except the tree at [2, 2], which will be inside the fence.

Example 2:

Input: trees = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]
Explanation: The fence forms a line that passes through all the trees.

Constraints:

• 1 <= trees.length <= 3000
• trees[i].length == 2
• 0 <= xi, yi <= 100
• All the given positions are unique.

Solutions (Rust)

1. Solution

use std::collections::HashSet;

impl Solution {
    pub fn outer_trees(trees: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let mut trees = trees;
        let mut stack = vec![];
        let mut used = HashSet::new();

        trees.sort_unstable();
        stack.push(trees[0].clone());
        used.insert(trees[0].clone());

        for i in 1..trees.len() {
            let (x0, y0) = (trees[i][0], trees[i][1]);

            while stack.len() > 1 {
                let (x1, y1) = (stack[stack.len() - 1][0], stack[stack.len() - 1][1]);
                let (x2, y2) = (stack[stack.len() - 2][0], stack[stack.len() - 2][1]);

                if (x1 - x2) * (y0 - y1) < (x0 - x1) * (y1 - y2) {
                    used.remove(&vec![x1, y1]);
                    stack.pop();
                } else {
                    break;
                }
            }

            used.insert(vec![x0, y0]);
            stack.push(vec![x0, y0]);
        }
        for i in (0..trees.len() - 1).rev() {
            let (x0, y0) = (trees[i][0], trees[i][1]);

            if i > 0 && used.contains(&vec![x0, y0]) {
                continue;
            }

            while stack.len() > 1 {
                let (x1, y1) = (stack[stack.len() - 1][0], stack[stack.len() - 1][1]);
                let (x2, y2) = (stack[stack.len() - 2][0], stack[stack.len() - 2][1]);

                if (x1 - x2) * (y0 - y1) < (x0 - x1) * (y1 - y2) {
                    used.remove(&vec![x1, y1]);
                    stack.pop();
                } else {
                    break;
                }
            }

            used.insert(vec![x0, y0]);
            stack.push(vec![x0, y0]);
        }

        used.into_iter().collect()
    }
}