README.md

1260. Shift 2D Grid

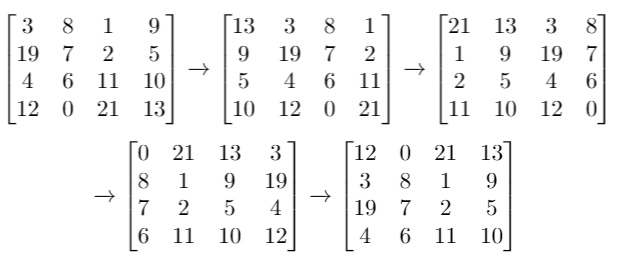
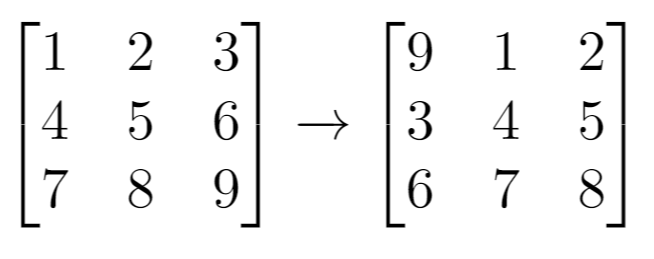Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] becomes at grid[i][j + 1].
• Element at grid[i][n - 1] becomes at grid[i + 1][0].
• Element at grid[n - 1][n - 1] becomes at grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

Solutions (Rust)

1. Solution

impl Solution {
    pub fn shift_grid(grid: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
        let (m, n) = (grid.len(), grid[0].len());
        let k = (k as usize) % (m * n);
        let mut ret = vec![vec![0; n]; m];

        for pos in 0..(m * n) {
            let tmp = (pos + m * n - k) % (m * n);
            ret[pos / n][pos % n] = grid[tmp / n][tmp % n];
        }

        ret
    }
}