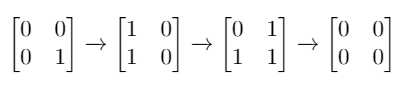README.md

1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 3
• mat[i][j] is either 0 or 1.

Solutions (Rust)

1. Solution

use std::collections::VecDeque;

impl Solution {
    pub fn min_flips(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut min_steps = vec![None; 1 << (m * n)];
        let mut deque = VecDeque::new();
        let mut bin_mat = 0;

        for row in 0..m {
            for col in 0..n {
                bin_mat |= (mat[row][col] as usize) << (row * n + col);
            }
        }

        min_steps[bin_mat] = Some(0);
        deque.push_back(bin_mat);

        while let Some(x) = deque.pop_front() {
            if x == 0 {
                break;
            }

            for row in 0..m {
                for col in 0..n {
                    let mut y = x;

                    y ^= 1 << (row * n + col);
                    y ^= ((row > 0) as usize) << (row * n + col - n);
                    y ^= ((row < m - 1) as usize) << (row * n + col + n);
                    y ^= ((col > 0) as usize) << (row * n + col - 1);
                    y ^= ((col < n - 1) as usize) << (row * n + col + 1);

                    if min_steps[y].is_none() {
                        min_steps[y] = Some(min_steps[x].unwrap() + 1);
                        deque.push_back(y);
                    }
                }
            }
        }

        min_steps[0].unwrap_or(-1)
    }
}