Skip to content

Latest commit

 

History

History
64 lines (53 loc) · 2.33 KB

README.md

File metadata and controls

64 lines (53 loc) · 2.33 KB
Raw

1373. Maximum Sum BST in Binary Tree

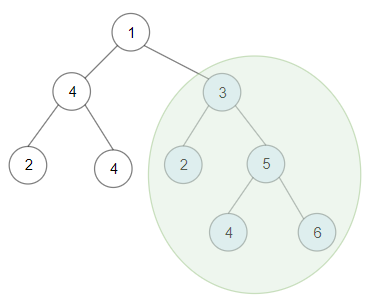
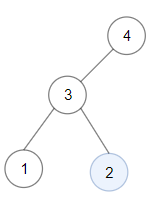
Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Constraints:

  • The number of nodes in the tree is in the range [1, 4 * 104].
  • -4 * 104 <= Node.val <= 4 * 104

Solutions (Python)

1. Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxSumBST(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> (bool, int, int, int, int):
            if root is None:
                return (True, 40001, -40001, 0, 0)

            isbstl, minl, maxl, suml, retl = dfs(root.left)
            isbstr, minr, maxr, sumr, retr = dfs(root.right)
            isbstt = isbstl and isbstr and root.val > maxl and root.val < minr

            if isbstt:
                sumt = suml + sumr + root.val
                return (True, min(minl, root.val), max(maxr, root.val), sumt, max(sumt, retl, retr))
            else:
                return (False, 0, 0, 0, max(retl, retr))

        return dfs(root)[4]