README.md

1761. Minimum Degree of a Connected Trio in a Graph

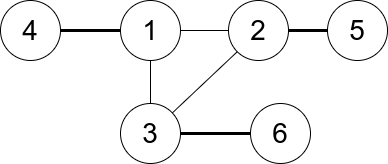
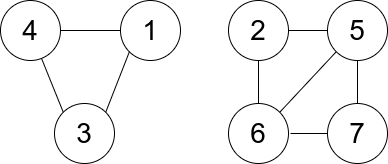
You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

• 2 <= n <= 400
• edges[i].length == 2
• 1 <= edges.length <= n * (n-1) / 2
• 1 <= ui, vi <= n
• ui != vi
• There are no repeated edges.

Solutions (Rust)

1. Solution

use std::collections::HashSet;

impl Solution {
    pub fn min_trio_degree(n: i32, edges: Vec<Vec<i32>>) -> i32 {
        let n = n as usize;
        let mut edges_set = HashSet::new();
        let mut count = vec![0; n + 1];
        let mut ret = -1;

        for i in 0..edges.len() {
            let (u, v) = (
                edges[i][0].min(edges[i][1]) as usize,
                edges[i][0].max(edges[i][1]) as usize,
            );

            edges_set.insert((u, v));
            count[u] += 1;
            count[v] += 1;
        }

        for i in 1..=n {
            for j in i + 1..=n {
                if !edges_set.contains(&(i, j)) {
                    continue;
                }

                for k in j + 1..=n {
                    if !edges_set.contains(&(i, k)) || !edges_set.contains(&(j, k)) {
                        continue;
                    }

                    let degree = count[i] + count[j] + count[k] - 6;

                    if ret == -1 || degree < ret {
                        ret = degree;
                    }
                }
            }
        }

        ret
    }
}