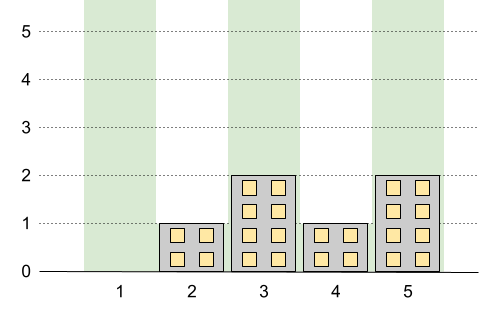README.md

1840. Maximum Building Height

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

• The height of each building must be a non-negative integer.
• The height of the first building must be 0.
• The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

Example 1:

Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

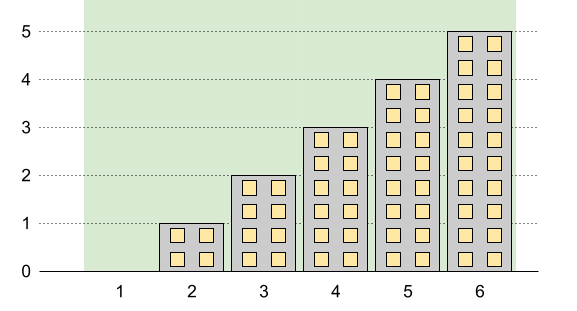
Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

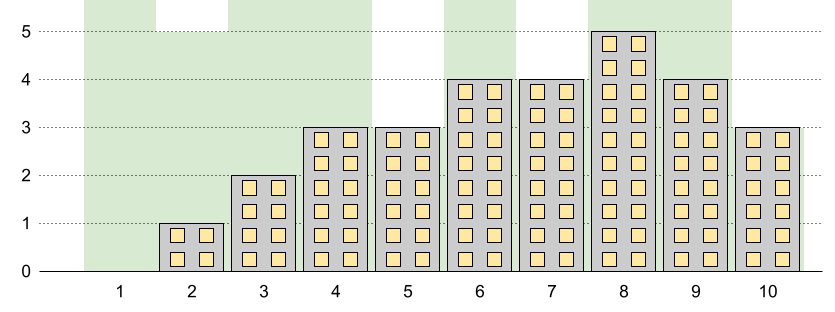
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

Constraints:

• 2 <= n <= 109
• 0 <= restrictions.length <= min(n - 1, 105)
• 2 <= idi <= n
• idi is unique.
• 0 <= maxHeighti <= 109

Solutions (Rust)

1. Solution

impl Solution {
    pub fn max_building(n: i32, mut restrictions: Vec<Vec<i32>>) -> i32 {
        restrictions.push(vec![1, 0]);
        restrictions.sort_unstable();
        if restrictions.last().unwrap()[0] != n {
            restrictions.push(vec![n, n - 1]);
        }

        for i in 1..restrictions.len() {
            restrictions[i][1] = restrictions[i][1]
                .min(restrictions[i - 1][1] + restrictions[i][0] - restrictions[i - 1][0]);
        }
        for i in (0..restrictions.len() - 1).rev() {
            restrictions[i][1] = restrictions[i][1]
                .min(restrictions[i + 1][1] + restrictions[i + 1][0] - restrictions[i][0]);
        }

        (0..restrictions.len() - 1)
            .map(|i| {
                (restrictions[i + 1][1] + restrictions[i][1] - restrictions[i][0]
                    + restrictions[i + 1][0])
                    / 2
            })
            .max()
            .unwrap()
    }
}