README.md

2428. Maximum Sum of an Hourglass

You are given an m x n integer matrix grid.

We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.

Note that an hourglass cannot be rotated and must be entirely contained within the matrix.

Example 1:

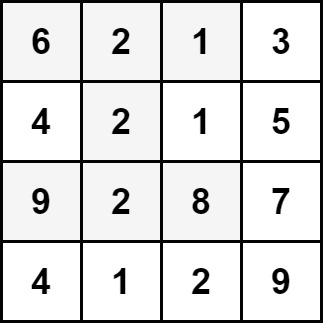
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
Output: 30
Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.

Example 2:

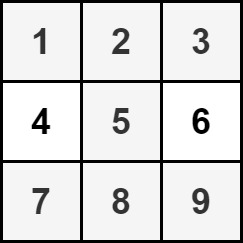
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: 35
Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.

Constraints:

• m == grid.length
• n == grid[i].length
• 3 <= m, n <= 150
• 0 <= grid[i][j] <= 106

Solutions (Rust)

1. Solution

impl Solution {
    pub fn max_sum(grid: Vec<Vec<i32>>) -> i32 {
        let mut ret = 0;

        for i in 1..grid.len() - 1 {
            for j in 1..grid[0].len() - 1 {
                ret = ret.max(
                    grid[i][j]
                        + grid[i - 1][j]
                        + grid[i + 1][j]
                        + grid[i - 1][j - 1]
                        + grid[i + 1][j - 1]
                        + grid[i - 1][j + 1]
                        + grid[i + 1][j + 1],
                );
            }
        }

        ret
    }
}