PriorityQueue.md

우선순위 큐(Priority Queue)와 힙(Heap)

1) 스택,큐와 비교

자료구조	탈출 순서
스택(Stack)	가장 먼저들어온게 가장 나중에
큐(Queue	가장 먼저들어온게 가장 먼저
우선순위 큐(Priority Queue)	우선순위가 높은 순서대로

2) 우선순위 큐의 구현방법

방법	삽입	삭제
리스트(list)	O(1)	O(N)
힙(heap)	O(logN)	O(logN)

따라서 heap은 N개의 원소를 전부넣고 전부 삭제하면 정렬의 효과를 볼 수 있습니다. 이때 시간 복잡도는 O(NlogN)입니다.

힙은 우선순위 큐를 구현하는 가장 효율적인 자료구조입니다.

3) 힙(heap)의 개념

• 완전이진트리(*) 자료구조의 일종

• 여러개의 값들중 최대값, 최소값을 빠르게 찾아내도록 만들어진 자료구조

• 반정렬상태(느슨한 정렬 상태)유지 : 부모노드가 항상 자식노드보다 큰(작은)상태

  *완전이진트리 : 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있는 상태 (왼쪽부터 차례대로 노드가 채워짐)

1. 최소힙(min heap) : 부모노드의 키 값이 자식노드의 키 값보다 작거나 같은 완전이진트리

2. 최대힙(max heap) : 부모노드의 키 값이 자식노드의 키 값보다 크거나 같은 완전이진트리

4) 힙(heap)의 구현

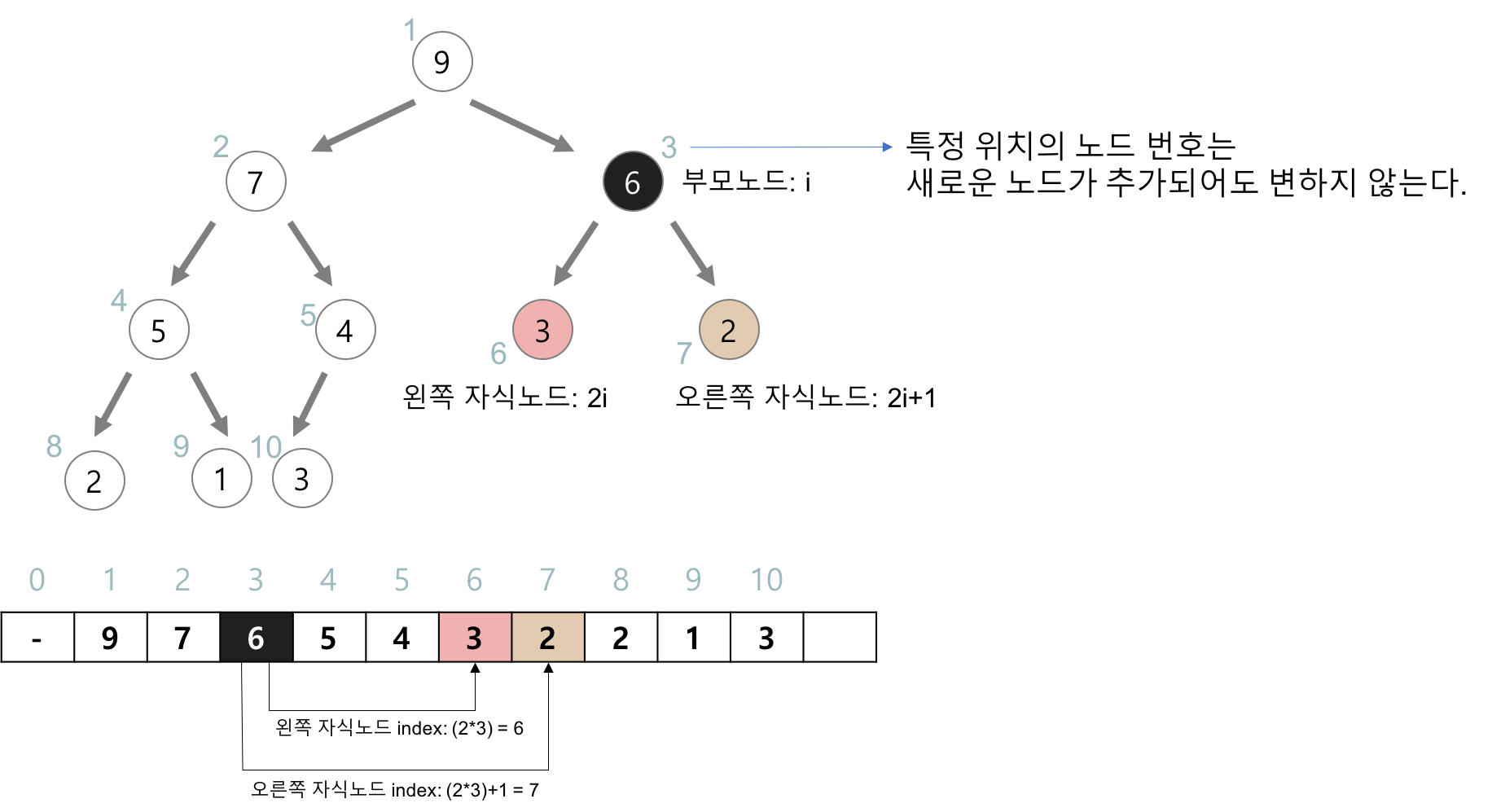
• 힙은 표준적으로 배열로 구현합니다
• 구현의 편의를 위해 배열의 첫 번째 인덱스 0은 사용하지 않는게 좋습니다.
• 부모노드와 자식노드의 관계 :
  • 왼쪽자식 인덱스 = (부모인덱스) * 2
  • 오른쪽자식 인덱스 = (부모인덱스) * 2 + 1
  • 부모인덱스 = (자식인덱스) // 2

5) 힙(heap): 삽입

• 힙에 새로운 요소가 들어오면 가장 마지막 노드에 들어갑니다
• 그렇게 삽입된 새로운 노드는 부모노드와의 비교를 통해 제자리를 찾게됩니다.

6) 힙(heap): 삭제

• 힙에서 요소를 삭제할 때는 항상 루트노드를 삭제
• 힙의 가장 마지막 노드를 루트노드로 가져와서 자식노드와 의 비교를 통해 제자리를 찾게합니다.

힙의 삽입과 삭제가 위와 같은 방식으로 이뤄지는 이유는 완전이진트리를 유지하기 쉽기 때문입니다.