204CountPrimes.md

204. Count Primes

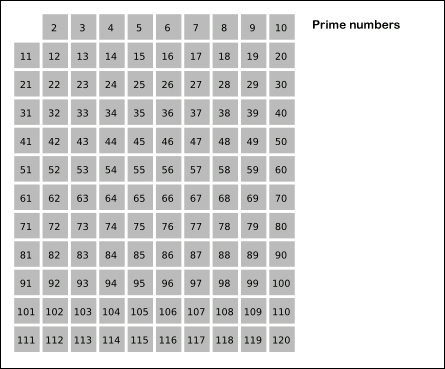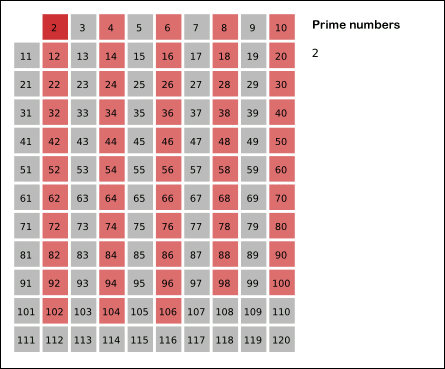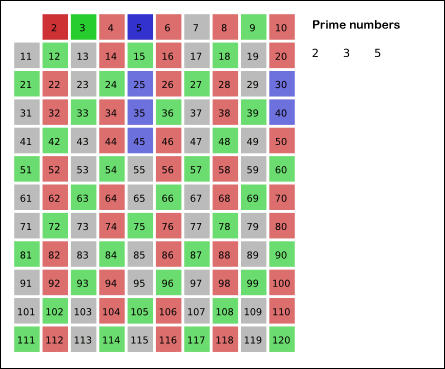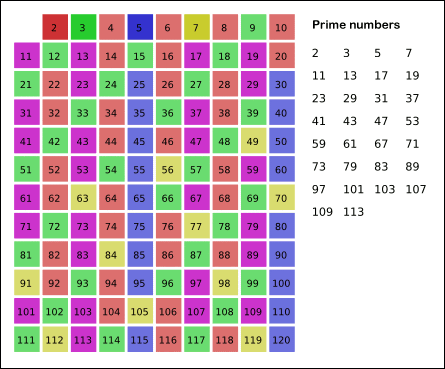
找出小于N的素数的数量。

1. $$ 暴力，空间O(1)，时间O(N^{1.5}) $$

   As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2.

   所有数N，都不可能被大于N/2整除。

   Let's write down all of 12's factors:

   2 × 6 = 12
   3 × 4 = 12
   4 × 3 = 12
   6 × 2 = 12
   

   As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.

   由上图可知，只需要考虑小于等于√N的数。

   证明：如果N可以被P整除，就存在数Q，满足N=P * Q。

   因为P<=Q，所以P<=√N。

   public int countPrimes(int n) {
      int count = 0;
      for (int i = 1; i < n; i++) {
         if (isPrime(i)) {
             count++;
         }
      }
      return count;
   }
   
   private boolean isPrime(int num) {
      if (num <= 1) return false;
      // Loop's ending condition is i * i <= num instead of i <= sqrt(num)
      // to avoid repeatedly calling an expensive function sqrt().
      for (int i = 2; i * i <= num; i++) {
         if (num % i == 0) {
             return false;
         }
      }
      return true;
   }

2. 筛选法（有点自底向上的味道），空间O(N)，时间O(NlogN)。

   

   We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well.

   观察2：所有2的倍数都不是素数，将它们标记位非素数。

   观察3：也一样。

   4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5.

   观察4：4不是一个素数，因为它可以被2整除，并且它和它的倍数已经被标记，所以直接跳过。

   In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3.

   观察5：我们可以从5 * 5 = 25开始标记，因为 5 * 2 = 10已经作为2的倍数被标记了，就正如15已经作为3的倍数被标记了。

   Therefore, if the current number is p, we can always mark off multiples of p starting at p^2, then in increments of p: p^2 + p, p^2 + 2p, ...

   因此，对于当前数字P，我们总是从P ^ 2平方开始标记，然后以P递增标记后面的倍数。

   The terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.

   回想第一种解法，可以得知：循环终止的条件是 P < √N，因为所有大于或等于√N的非素数都肯定已经被标记了。

   public int countPrimes(int n) {
       if(n <= 2) {
           return 0;
       }
       boolean[] notPrime = new boolean[n];
       // Loop's ending condition is i * i < n instead of i < sqrt(n)
       // to avoid repeatedly calling an expensive function sqrt().
       for (int i = 2; i * i < n; i++) {
           if (notPrime[i]) {
               continue;
           }
           for (int j = i * i; j < n; j += i) {
               notPrime[j] = true;
           }
       }
       int count = 0;
       for (int i = 2; i < n; i++) {
           if (!notPrime[i]) {
               count++;
           }
       }
       return count;
   }