-
Notifications
You must be signed in to change notification settings - Fork 71
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
dot_product = s_loss_old - s_loss_new but s_loss_new - s_loss_old? #6
Comments
|
Where is that from? According to the original code, it is s_loss_new - s_loss_old: where shadow is defined as: |
|
@zwd973 I can't fully follow your derivation. But this is the formula used in the original code, as stated above. I believe it is correct as is. Here's the derivation: First order Taylor: let f(x) be the cross entropy function, x is the new parameters this is new cross entropy minus old. |
|
|
@zwd973 You're right, I missed a negative. Interesting. The original author's code is wrong here then |
|
OK, thanks. |
|
@kekmodel this might be why it got worse? Though Im not sure how the author was able to replicate results |
|
I agree. I thought that the sign changes in the process of calculating |
|
@kekmodel Hello, how about the new result? |
|
Unfortunately, all test accuracy is about 94.4. The mpl loss doesn't seem to work. I'll have to wait until the author's code update. |
|
@kekmodel thats unfortunate to hear. But thank you for all your work thus far. The number of discrepancies in the original code make things quite difficult. |
|
If I am not mistaken, then the first order Taylor expansion goes as where h is described above as the gradient. This already is a problem since on the right hand side it is not the dot product between the gradient on the new parameters and the gradient on the old parameters. It is more the gradient on the old parameters squared, if I understand correctly. From that perspective the first order Taylor approximation does not make sense. Can you confirm or tell me if and where I am wrong? |
You’re correct from what I can see. Sorry, I did the derivation quickly and haphazardly, which is why it’s wrong lol. This quantity still has meaning since h is the gradient produced by the loss on the unlabeled target and this is the loss on the labeled data. So we’re essentially trying to get the teacher to produce the same loss as if the student was training on labeled data, but this also doesn’t seem to be what was derived in the paper. There’s supposed to be a time offset |
|
About your derivations. I do not see anything wrong with @dgedon's derivation.
Comparing this to my derivation below, it looks like the difference is in the very first place, where you start at About Taylor. My understanding is as follows. Using your notations,
About using soft labels. If you use soft labels, you do not even need Taylor or the log-gradient trick, because the entire process is differentiable and you can do some Hessian/Jacobian vector product tricks instead. In my implementation for this, I created shadow variables that hold the student's parameters, then build a computational graph to compute the gradients of these shadow variables using For ugly reasons (exceeding graph proto size limits, if you are curious), this implementation did not run with GShard which we used for model parallelism, so we decided to do approximation instead. Update code. I got some insider push backs because I was trying to update the code and release the trained checkpoints at the same time. I apologize for the delay, and will try to push on this more. |
|
Thanks @hyhieu. About Taylor expansion: It works out nicely when you start in your way. However, I have two follow-up remarks/question on it:
About Soft Labels: I have to think this a bit more through. In your paper in (10) you have instead of a one-hot encoding with hard labels for \hat{y}_u just a 'smoothed' version when using soft labels. From this point I don't understand how this changes the derivation. |
@dgedon For the second question, I think we are approximating the red box(gradients of loss on labeled data wrt updated parameters). So when using finite difference, we should use the same data(labeled data) with different parameters(old/new). |
|
@kekmodel Hi, Thanks for the implementation! |
|
I think that the correct formula is old-new based on the several derivations that have been done here. But, I don't think the MPL Loss really has an effect either way. From what I can tell, based on the experiments here, my own experiments, and the reference code being flipped but still replicating results. I have a custom implementation I did at work, for our datasets, I was able to get good results with it. It beat UDA alone and other contrastive techniques I tried. As an aside, it only worked if I used a much larger unlabeled batch size (7x multiplier) this is similar to the released code, but the paper claimed it should work 1 to 1. I ran an extensive hyperparameter search to see if MPL Loss helps at all, it seemed to make no real difference no matter the settings (at least on the several internal problems I tried it on). They are of comparable size and difficulty to CIFAR-10. One is much larger and closer to ImageNet. I also tried several networks. The hyperparameter search did not tend towards keeping it or not, there was no statistical difference among the temperatures of the loss, including a temp 1.0 which disables the loss, and taking the best settings with or without MPL loss active seems to make no difference. Maybe it helps for ImageNet or Cifar-10, but, experiments here don't support that. It certainly does not help for the various problems I tried it on. That being said, the procedure itself works quite well, just not due to MPL Loss I think. @kekmodel not sure if you have run experiments with larger unlabeled batch sizes, but it's probably worth trying, as I couldn't get it to work without this, but it performs better than anything else I tried, under this setting. |
|
@monney Thank you for your valuable insights. I have some follow-up questions regarding your experiments.
Thanks : ) |
all my experiments for both were done with larger unlabeled batch sizes and similar training. The benefit almost certainly comes from the self distillation procedure, and the unique finetuning phase of MPL.
It works, and works better the other contrastive learning methods I’ve tried (UDA, BYOL, SimCLR, NoisyStudent). But the actual MPL loss seems to have no major effect on the results and I think the other differences of this paper are largely responsible for the increased performance. My guess is in the end the paper ends up being very similar to fixmatch. cheers |
|
@monney I see. That's a little surprising as the MPL objective makes a lot of sense to me. Also, figure.3 in the appendix breaks down the contribution of each component, and it shows that whether using the MPL loss will make a huge difference. |
|
@zxhuang97 it makes a lot of sense to me as well, so confusing. I’ll update if I find bugs or anything, but I’ve done a lot of testing. The breakdown in fig 3. will include the entire MPL procedure I’m pretty sure, so it’s difficult to isolate just the loss contribution. UDA is just the standard UDA procedure. |
I guess you're right. The UDA module in the official implementation doesn't include the teacher&student stuff, so it's not really a fair comparison. Thank you for the information! |
|
When training converges, theoretically, both s_loss_old - s_loss_new and s_loss_new - s_loss_old will be zero, is this the way it should be? Has anyone tried the none Taylor approximation way to calculate the dot product? Does it work? |
|
@jacobunderlinebenseal |
I am planning to use the MPL loss in my own project, and I wanted to kindly ask for your opinion: in your experience, have you found this method to deliver effective results? I just wanted to make sure I understand its impact accurately before implementing it. |



Hello, thanking for your pytorch implement of MPL. I think the dot_prodoct should be s_loss_old - s_loss_new but s_loss_new - s_loss_old for the reason here
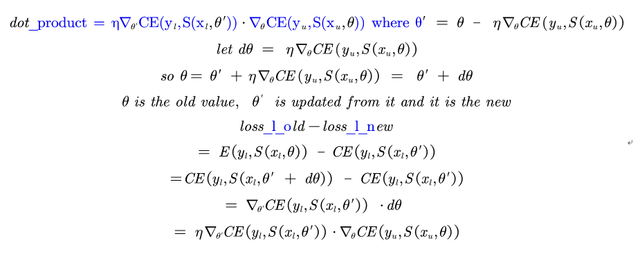
just flip a coin
Am I wrong?
The text was updated successfully, but these errors were encountered: