Skip to content

Latest commit

 

History

History
148 lines (111 loc) · 14.7 KB

README.md

File metadata and controls

148 lines (111 loc) · 14.7 KB

理解算法与数据结构，学习不同编程语言 English

根据不同编程语言来学习数据结构和算法，包括 C Java Python JavaScript Go TypeScript 等，提供充分注释说明。

本项目特点：

  1. 涵盖了数值计算、字符查找、树遍历、排序、动态规划等不同算法。
  2. 每个算法都有多种语言的实现，通过算法与数据结构理解不同语言的特色。
  3. 例子逐一，适合学生或程序员学习和分析，提升编程水平。

算法概览

常见的算法有哪些？

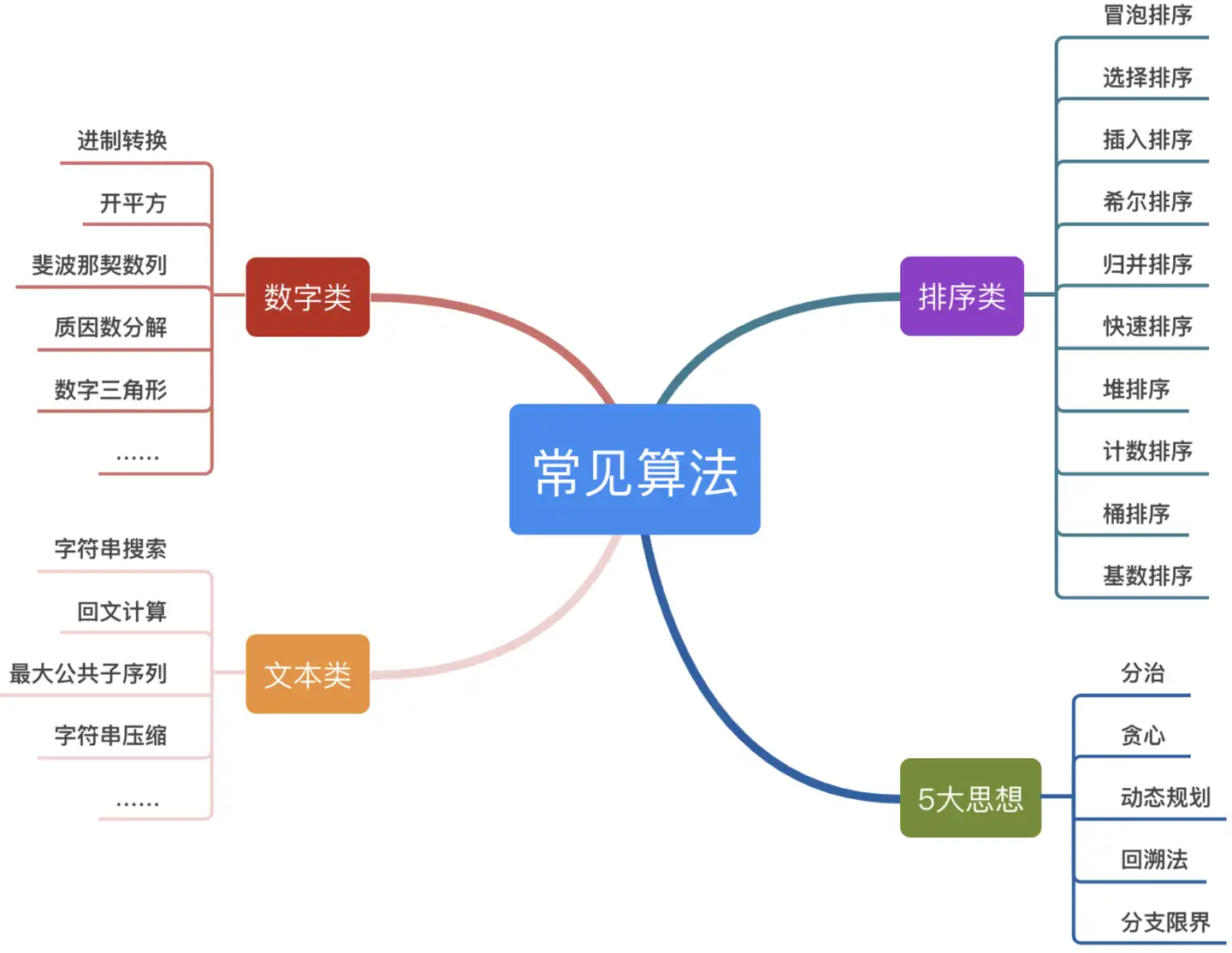
  • 文本查找：包括线性搜索、二分搜索、树形搜索、最大公共子序列、回文计算等，主要针对字符串查找。
  • 数学计算：包括进制转换、开平方、斐波那契数列、质因数分解、数字三角形等，主要进行数值计算。
  • 排序算法：包括冒泡、选择、插入、希尔、归并、快速、堆、计数、桶、基数等，用于按顺序排列数据。
  • 其他算法：包括动态规划、贪心算法、分治算法、回溯算法、图算法（如广度优先搜索、深度优先搜索、Dijkstra算法、Kruskal算法等），此外还包括机器学习和人工智能算法，如分类算法、聚类算法、深度学习、强化学习等。

算法概览

常见算法思想

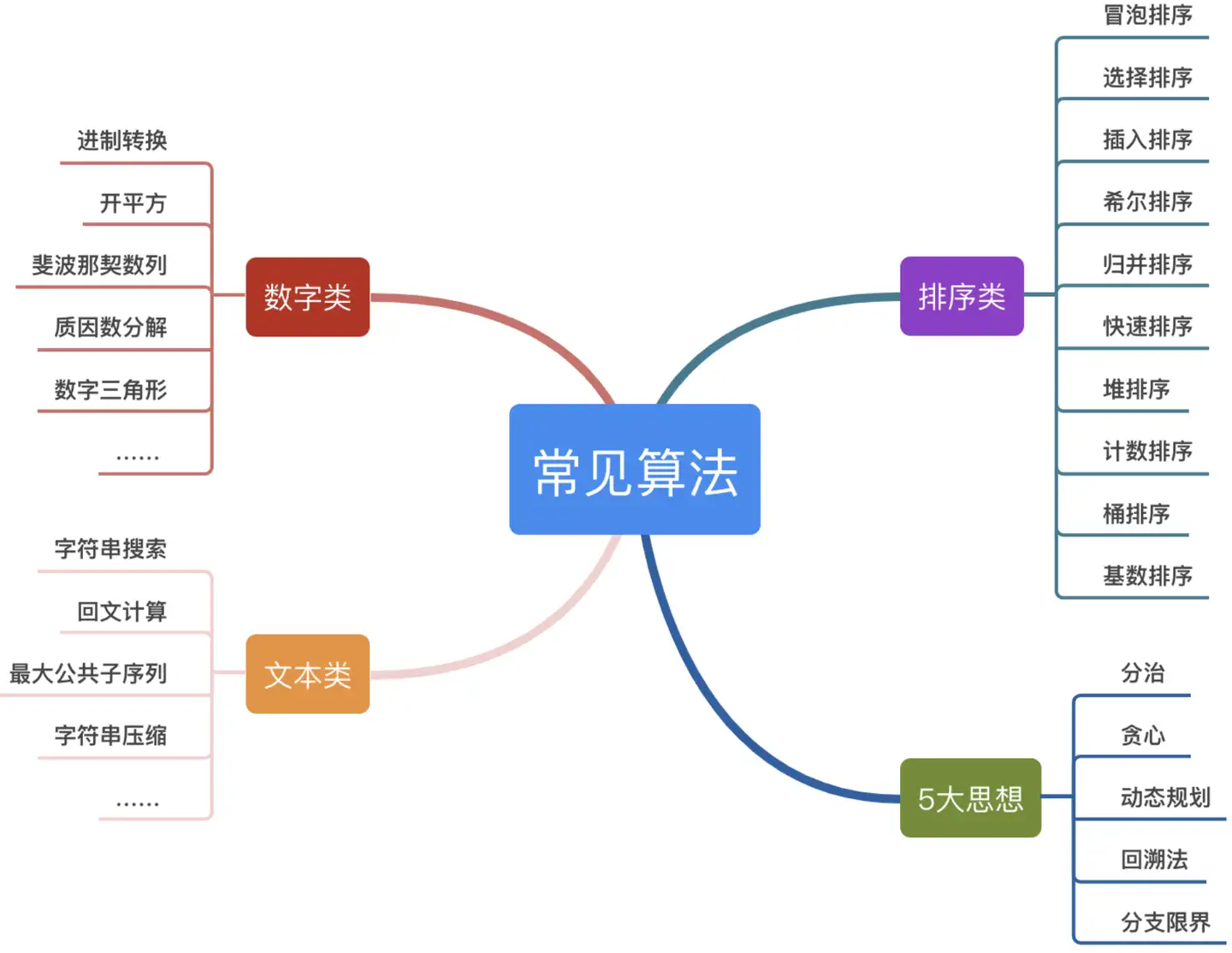
  • 贪心算法：一种通过每次选择局部最优解来期望得到全局最优解的方法。
  • 分治算法：将问题分解为较小的子问题，独立解决后再合并结果。
  • 动态规划：通过将复杂问题分解为更简单的重叠子问题来求解。
  • 回溯算法：通过逐步构建候选解并放弃那些无法满足条件的方案来解决问题。
  • 图算法：包括广度优先搜索、深度优先搜索、Dijkstra算法、Kruskal算法等，用于解决图相关问题。
  • 分支限界法：一种组合优化问题的求解方法，通过系统地探索搜索树的分支来解决问题。

详细信息见：10大算法思想

10大经典排序算法

排序算法 C语言版 JS版 Python版 Java版 TS版 Go版 时间复杂度（平均/最坏） 空间复杂度 稳定性 适用场景
冒泡排序 bubble sort C JS Python Java TS Go O(n²) / O(n²) O(1) ✅ 适用于小规模数据排序，教学用途
插入排序 insert sort C JS Python Java TS Go O(n²) / O(n²) O(1) ✅ 适用于小规模数据，少量元素已基本有序的情况
选择排序 selection sort C JS Python Java TS Go O(n²) / O(n²) O(1) ❌ 适用于小规模数据，数据交换次数较少
堆排序 heap sort C JS Python Java TS Go O(n log n) / O(n log n) O(1) ❌ 适用于优先队列、TOP K问题
快速排序 quick sort C JS Python Java TS Go O(n log n) / O(n²) O(log n) ❌ 适用于一般排序场景，性能优异但不稳定
归并排序 merge sort C JS Python Java TS Go O(n log n) / O(n log n) O(n) ✅ 适用于大数据量排序，适合外部排序
计数排序 counting sort C JS Python Java TS Go O(n + k) / O(n + k) O(k) ✅ 适用于数据范围有限的整数排序
基数排序 radix sort C JS Python Java TS Go O(nk) / O(nk) O(n + k) ✅ 适用于大规模整数排序，如身份证号、手机号排序
桶排序 bucket sort C JS Python Java TS Go O(n + k) / O(n²) O(n + k) ✅ 适用于数据范围均匀分布的排序
希尔排序 shell sort C JS Python Java TS Go O(n log n) / O(n²) O(1) ❌ 适用于中等规模数据排序，适合半有序数据

字符串搜索与查找

算法 C语言版 Go语言版 JS版 Python版 Java版 TS版 时间复杂度（平均/最坏） 空间复杂度 适用场景
朴素搜索 C Go JS Python Java TS O(mn) / O(mn) O(1) 适用于小规模文本搜索
二分查找 C Go JS Python Java TS O(log n) / O(log n) O(1) 适用于已排序数组的查找
KMP搜索 C Go JS Python Java TS O(n + m) / O(n + m) O(m) 适用于大规模文本搜索

树搜索与遍历

算法 C语言版 JS版 Python版 Java版 TS版 时间复杂度（平均/最坏） 空间复杂度 适用场景
二叉树遍历 C JS Python Java TS O(n) / O(n) O(n) 适用于树结构数据的遍历，如 XML 解析、文件系统遍历

质因数分解

语言 代码链接 复杂度 适用场景
C factor.c O(√n) 计算大整数的质因数分解
C++ factor.cpp O(√n) 适用于高效数学计算
JavaScript factor.js O(√n) Web 端数论计算
TypeScript PrimeFactor.ts O(√n) 适用于前端或 Node.js 计算
Go factor.go O(√n) 适用于后端服务计算
Python factor.py O(√n) 适用于科学计算、数据分析
Java Factor.java O(√n) 适用于企业级应用计算
Kotlin factor.kt O(√n) 适用于 Android 和后端计算
Dart factor.dart O(√n) 适用于 Flutter 应用
Swift factor.swift O(√n) 适用于 iOS/macOS 开发
Objective-C factor.m O(√n) 适用于老版本 iOS/macOS
Rust factor.rs O(√n) 适用于高性能计算

数组列表去重复项

语言 代码链接 时间复杂度 适用场景
C unique.c O(n log n) 适用于嵌入式开发
Go unique.go O(n log n) 适用于高并发场景
JS unique.js O(n) 适用于前端数据处理
Python unique.py O(n) 适用于数据清洗、分析
Java UniqueArray.java O(n log n) 适用于企业级应用
TypeScript UniqueArray.ts O(n) 适用于前端 TypeScript 项目
Dart unique.dart O(n) 适用于 Flutter 应用
Rust unique.rs O(n) 适用于高性能计算

递归

算法 代码链接 时间复杂度 空间复杂度 适用场景
简单递归 C O(2^n) O(n) 适用于分治算法、树和图的遍历、回溯问题

数学计算

算法 代码链接 时间复杂度 空间复杂度 适用场景
数学计算 C O(n) O(1) 适用于数论、加法、乘法、大整数计算等

日期与日历

算法 代码链接 时间复杂度 空间复杂度 适用场景
日期与日历 C O(1) O(1) 适用于日期计算、节假日推算、日期转换等

数据结构

数据结构是数据的组织和存储的方式，也就是把数据聚合在一起，以便进行加工整理。不同的数据结构，对其访问、插入、删除等操作的效率不同。通过选择合适的数据结构，可以高效地处理数据。详见：数据结构概述

数据结构 描述 结构特点 访问效率 插入/删除效率
Array (数组) 具有相同数据类型的元素集合，支持按索引随机访问 连续内存存储，支持线性或非线性 O(1) O(n)
Linked List (链表) 数据以链式结构存储，通过指针连接，分为单向链表、双向链表和循环链表 线性结构，内存不连续 O(n) O(1) (头部) / O(n) (中间)
Tree (树) 树状数据集合，节点按层级关系组织，常见类型包括二叉树、二叉搜索树、平衡树等 非线性结构，一个根节点，子节点数量不限 O(log n) O(log n)
Heap (堆) 一种特殊的完全二叉树，满足堆序性（最大堆或最小堆），常用于优先队列 非线性结构，支持按最值高效操作 O(1) (取堆顶) O(log n)
Stack (栈) 后进先出 (LIFO) 的数据集合 线性结构，顺序或链式存储，仅允许在栈顶操作 O(1) O(1)
Queue (队列) 先进先出 (FIFO) 的数据集合 线性结构，顺序或链式存储，支持在队尾插入、队头删除 O(1) O(1)
Graph (图) 由节点（顶点）和边组成的图形数据结构，常见存储方式为邻接表或邻接矩阵 非线性结构，节点间可多对多连接 O(1) (邻接矩阵) / O(n) (邻接表) O(1) (邻接矩阵) / O(n) (邻接表)
Hash (散列) 通过哈希函数将键映射到存储位置的数据结构，支持快速查找、插入和删除 线性结构，通过哈希键值映射 O(1) (均摊) O(1) (均摊)
Struct (结构体) 组合多种类型的数据，形成一个整体，常用于表示复杂对象 自定义结构，字段固定，包含多种数据类型 O(1) O(1)
List (列表) 有序集合，允许重复元素，支持索引访问 线性结构，元素按插入顺序存储 O(1) (末尾插入)，O(n) (中间插入/删除) O(1) (索引访问)，O(n) (查找)
Set (集合) 无序集合，不允许重复元素，支持高效查找 线性结构，基于哈希或树实现 O(1) (哈希实现)，O(log n) (树实现) O(1) (哈希实现)，O(log n) (树实现)
Map (映射) 存储键值对的数据结构，支持快速查找、插入和删除 关联数组，基于哈希或平衡树实现 O(1) (哈希实现)，O(log n) (树实现) O(1) (哈希实现)，O(log n) (树实现)

相关链接

欢迎加入共建

仓库： https://github.com/microwind/algorithms 站点： https://microwind.github.io/algorithms

如果您对本项目感兴趣请加我，欢迎一起共建！ If you are interested in this project, please add me. I welcome you to build it together!

wechat: springbuild

邮件: [email protected] or [email protected]