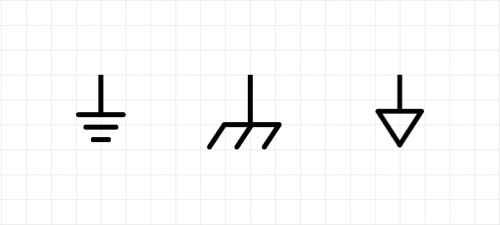nodal_analysis.md

Nodal Analysis

In the nodal analysis, node voltages are calculated by solving the Kirchhoff's Current Law (KCL) equations obtained from each node.

Method includes the following steps:

• Choose a reference node (ground)
• Label node voltages
• Write KCL equations for each node except the ground node.

(For reference check Nodal Analysis e-book).

1-Choose a reference node (or ground node)

• It is best to choose ground node as the node interconnects the most branches.
• The ground node is usually at the bottom of circuit.
• Label ground with one of the symbols below:

2-Assign node voltages

Give label to each node except the reference node.

3- Write KCL equations

• write KCL equations (the most practical way is to use negative sign for the currents entering to the node), positive sign for currents exiting from the node).
• After defining KCL for each node, the equations can be put in matrix form and the problem can be solved.

4-Solve

Methods for solving system of linear equations:

• Elimination Method : Simplest but not really scalable to more complex equations
• Row reduction: A systematical way of elimination, can be applied to more complex cases, but it's time consuming.
• Cramer's Rule (example): Practical for up to 3x3 matrices.
• Inverse Matrix Method: Scalable to even the most complex cases, but you'll need a calculator or computer.

Example 1:

Calculate the node voltages for the following circuit¹:

Answer: V1= 40/3 V, V2= 20 V

Matrix Equations

Example:

Apply the nodal analysis in the following circuit: This is some text.

• Define the bottom node as the reference node
• Apply KCL for each node:

Node a: $$-I_1 + \frac{V_a}{R_1} + \frac{V_a-V_b}{R_2} = 0 $$

Node b: $$\frac{V_b-V_a}{R_2} + \frac{V_b}{R_3} + \frac{V_b-V_c}{R_4} = 0 $$

Node c: $$ \frac{V_c-V_b}{R_4} + I_2 = 0 $$

Then everything can be put into matrix form:

$$\begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2} & -\frac{1}{R_2} & 0 \ -\frac{1}{R_2} & \frac{1}{R_2}+ \frac{1}{R_3}+\frac{1}{R_4} & -\frac{1}{R_4} \\ 0 & -\frac{1}{R_4} & \frac{1}{R_4} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \\ \end{bmatrix} + \begin{bmatrix} -I_1 \\ 0 \\ I_2 \\ \end{bmatrix} =0$$

which is equivalent to $$\begin{bmatrix} \frac{1}{R_1}+\frac{1}{R_2} & -\frac{1}{R_2} & 0 \ -\frac{1}{R_2} & \frac{1}{R_2}+ \frac{1}{R_3}+\frac{1}{R_4} & -\frac{1}{R_4} \ 0 & -\frac{1}{R_4} & \frac{1}{R_4} \end{bmatrix} \begin{bmatrix} V_a \ V_b \ V_c \ \end{bmatrix}

\begin{bmatrix} I_1 \ 0 \ -I_2 \ \end{bmatrix} $$

For convenience instead of resistance, conductance can also be used:

$$G = \frac{1}{R}$$

Thus, the equation becomes:

$$\begin{bmatrix} G_1+G_2 & -G_2 & 0 \ -G_2 & G_2+ G_3+G_4 & -G_4 \ 0 & -G_4 & G_4 \end{bmatrix} \begin{bmatrix} V_a \ V_b \ V_c \ \end{bmatrix}

\begin{bmatrix} I_1 \ 0 \ -I_2 \ \end{bmatrix} $$

Note that, this is a classic matrix equation: $$AX = B$$ This equation can be solved as: $$X = A^{-1}B$$

where \(A^{-1}\) is the inverse of matrix A. In order to get the inverse of a matrix it has to be a square matrix. Furthermore, due to KCL applied A matrix in an electric circuit will be symmetrical.

Footnotes

1. Alexander&Sadiku, 2012, pg84. ↩