encoder-decoder.md

title	thumbnail
Transformer-based Encoder-Decoder Models	/blog/assets/05_encoder_decoder/thumbnail.png

Transformers-based Encoder-Decoder Models

Published October 08, 2020. Update on GitHub

patrickvonplaten Patrick von Platen

Transformer-based Encoder-Decoder Models

!pip install transformers==4.2.1
!pip install sentencepiece==0.1.95

The transformer-based encoder-decoder model was introduced by Vaswani et al. in the famous Attention is all you need paper and is today the de-facto standard encoder-decoder architecture in natural language processing (NLP).

Recently, there has been a lot of research on different pre-training objectives for transformer-based encoder-decoder models, e.g. T5, Bart, Pegasus, ProphetNet, Marge, etc..., but the model architecture has stayed largely the same.

The goal of the blog post is to give an in-detail explanation of how the transformer-based encoder-decoder architecture models sequence-to-sequence problems. We will focus on the mathematical model defined by the architecture and how the model can be used in inference. Along the way, we will give some background on sequence-to-sequence models in NLP and break down the transformer-based encoder-decoder architecture into its encoder and decoder parts. We provide many illustrations and establish the link between the theory of transformer-based encoder-decoder models and their practical usage in 🤗Transformers for inference. Note that this blog post does not explain how such models can be trained - this will be the topic of a future blog post.

Transformer-based encoder-decoder models are the result of years of research on representation learning and model architectures. This notebook provides a short summary of the history of neural encoder-decoder models. For more context, the reader is advised to read this awesome blog post by Sebastion Ruder. Additionally, a basic understanding of the self-attention architecture is recommended. The following blog post by Jay Alammar serves as a good refresher on the original Transformer model here.

At the time of writing this notebook, 🤗Transformers comprises the encoder-decoder models T5, Bart, MarianMT, and Pegasus, which are summarized in the docs under model summaries.

The notebook is divided into four parts:

• Background - A short history of neural encoder-decoder models is given with a focus on RNN-based models.
• Encoder-Decoder - The transformer-based encoder-decoder model is presented and it is explained how the model is used for inference.
• Encoder - The encoder part of the model is explained in detail.
• Decoder - The decoder part of the model is explained in detail.

Each part builds upon the previous part, but can also be read on its own.

Background

Tasks in natural language generation (NLG), a subfield of NLP, are best expressed as sequence-to-sequence problems. Such tasks can be defined as finding a model that maps a sequence of input words to a sequence of target words. Some classic examples are summarization and translation. In the following, we assume that each word is encoded into a vector representation. \(n\) input words can then be represented as a sequence of \(n\) input vectors:

$$\mathbf{X}_{1:n} = {\mathbf{x}_1, \ldots, \mathbf{x}_n}.$$

Consequently, sequence-to-sequence problems can be solved by finding a mapping \(f\) from an input sequence of \(n\) vectors \(\mathbf{X}{1:n}\) to a sequence of \(m\) target vectors \(\mathbf{Y}{1:m}\), whereas the number of target vectors \(m\) is unknown apriori and depends on the input sequence:

$$ f: \mathbf{X}{1:n} \to \mathbf{Y}{1:m}. $$

Sutskever et al. (2014) noted that deep neural networks (DNN)s, "despite their flexibility and power can only define a mapping whose inputs and targets can be sensibly encoded with vectors of fixed dimensionality." \({}^1\)

Using a DNN model \({}^2\) to solve sequence-to-sequence problems would therefore mean that the number of target vectors \(m\) has to be known apriori and would have to be independent of the input \(\mathbf{X}{1:n}\). This is suboptimal because, for tasks in NLG, the number of target words usually depends on the input \(\mathbf{X}{1:n}\) and not just on the input length \(n\). E.g., an article of 1000 words can be summarized to both 200 words and 100 words depending on its content.

In 2014, Cho et al. and Sutskever et al. proposed to use an encoder-decoder model purely based on recurrent neural networks (RNNs) for sequence-to-sequence tasks. In contrast to DNNS, RNNs are capable of modeling a mapping to a variable number of target vectors. Let's dive a bit deeper into the functioning of RNN-based encoder-decoder models.

During inference, the encoder RNN encodes an input sequence \(\mathbf{X}_{1:n}\) by successively updating its hidden state \({}^3\). After having processed the last input vector \(\mathbf{x}_n\), the encoder's hidden state defines the input encoding \(\mathbf{c}\). Thus, the encoder defines the mapping:

$$ f_{\theta_{enc}}: \mathbf{X}_{1:n} \to \mathbf{c}. $$

Then, the decoder's hidden state is initialized with the input encoding and during inference, the decoder RNN is used to auto-regressively generate the target sequence. Let's explain.

Mathematically, the decoder defines the probability distribution of a target sequence \(\mathbf{Y}_{1:m}\) given the hidden state \(\mathbf{c}\):

$$ p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}). $$

By Bayes' rule the distribution can be decomposed into conditional distributions of single target vectors as follows:

$$ p_{\theta_{dec}}(\mathbf{Y}{1:m} |\mathbf{c}) = \prod{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c}). $$

Thus, if the architecture can model the conditional distribution of the next target vector, given all previous target vectors:

$$ p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c}), \forall i \in {1, \ldots, m},$$

then it can model the distribution of any target vector sequence given the hidden state \(\mathbf{c}\) by simply multiplying all conditional probabilities.

So how does the RNN-based decoder architecture model \(p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})\)?

In computational terms, the model sequentially maps the previous inner hidden state \(\mathbf{c}_{i-1}\) and the previous target vector \(\mathbf{y}_i\) to the current inner hidden state \(\mathbf{c}_i\) and a logit vector \(\mathbf{l}_i\) (shown in dark red below):

$$ f_{\theta_{\text{dec}}}(\mathbf{y}{i-1}, \mathbf{c}{i-1}) \to \mathbf{l}_i, \mathbf{c}_i.$$

\(\mathbf{c}_0\) is thereby defined as \(\mathbf{c}\) being the output hidden state of the RNN-based encoder. Subsequently, the softmax operation is used to transform the logit vector \(\mathbf{l}_i\) to a conditional probablity distribution of the next target vector:

$$ p(\mathbf{y}i | \mathbf{l}i) = \textbf{Softmax}(\mathbf{l}i), \text{ with } \mathbf{l}i = f{\theta{\text{dec}}}(\mathbf{y}{i-1}, \mathbf{c}{\text{prev}}). $$

For more detail on the logit vector and the resulting probability distribution, please see footnote \({}^4\). From the above equation, we can see that the distribution of the current target vector \(\mathbf{y}i\) is directly conditioned on the previous target vector \(\mathbf{y}{i-1}\) and the previous hidden state \(\mathbf{c}{i-1}\). Because the previous hidden state \(\mathbf{c}{i-1}\) depends on all previous target vectors \(\mathbf{y}0, \ldots, \mathbf{y}{i-2}\), it can be stated that the RNN-based decoder implicitly (e.g. indirectly) models the conditional distribution \(p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})\).

The space of possible target vector sequences \(\mathbf{Y}{1:m}\) is prohibitively large so that at inference, one has to rely on decoding methods \({}^5\) that efficiently sample high probability target vector sequences from \(p{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c})\).

Given such a decoding method, during inference, the next input vector \(\mathbf{y}i\) can then be sampled from \(p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c})\) and is consequently appended to the input sequence so that the decoder RNN then models \(p_{\theta_{\text{dec}}}(\mathbf{y}{i+1} | \mathbf{Y}{0: i}, \mathbf{c})\) to sample the next input vector \(\mathbf{y}_{i+1}\) and so on in an auto-regressive fashion.

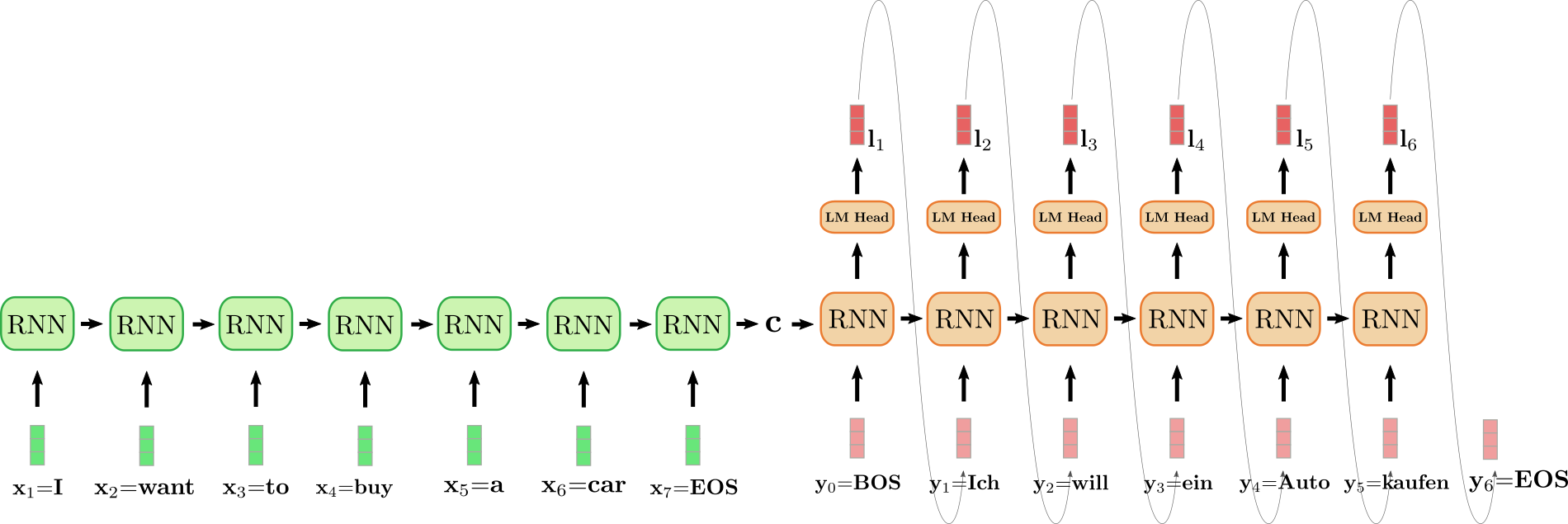
An important feature of RNN-based encoder-decoder models is the definition of special vectors, such as the \(\text{EOS}\) and \(\text{BOS}\) vector. The \(\text{EOS}\) vector often represents the final input vector \(\mathbf{x}_n\) to "cue" the encoder that the input sequence has ended and also defines the end of the target sequence. As soon as the \(\text{EOS}\) is sampled from a logit vector, the generation is complete. The \(\text{BOS}\) vector represents the input vector \(\mathbf{y}_0\) fed to the decoder RNN at the very first decoding step. To output the first logit \(\mathbf{l}_1\), an input is required and since no input has been generated at the first step a special \(\text{BOS}\) input vector is fed to the decoder RNN. Ok - quite complicated! Let's illustrate and walk through an example.

The unfolded RNN encoder is colored in green and the unfolded RNN decoder is colored in red.

The English sentence "I want to buy a car", represented by \(\mathbf{x}_1 = \text{I}\), \(\mathbf{x}_2 = \text{want}\), \(\mathbf{x}_3 = \text{to}\), \(\mathbf{x}_4 = \text{buy}\), \(\mathbf{x}_5 = \text{a}\), \(\mathbf{x}_6 = \text{car}\) and \(\mathbf{x}_7 = \text{EOS}\) is translated into German: "Ich will ein Auto kaufen" defined as \(\mathbf{y}_0 = \text{BOS}\), \(\mathbf{y}_1 = \text{Ich}\), \(\mathbf{y}_2 = \text{will}\), \(\mathbf{y}_3 = \text{ein}\), \(\mathbf{y}_4 = \text{Auto}, \mathbf{y}_5 = \text{kaufen}\) and \(\mathbf{y}_6=\text{EOS}\). To begin with, the input vector \(\mathbf{x}_1 = \text{I}\) is processed by the encoder RNN and updates its hidden state. Note that because we are only interested in the final encoder's hidden state \(\mathbf{c}\), we can disregard the RNN encoder's target vector. The encoder RNN then processes the rest of the input sentence \(\text{want}\), \(\text{to}\), \(\text{buy}\), \(\text{a}\), \(\text{car}\), \(\text{EOS}\) in the same fashion, updating its hidden state at each step until the vector \(\mathbf{x}_7={EOS}\) is reached \({}^6\). In the illustration above the horizontal arrow connecting the unfolded encoder RNN represents the sequential updates of the hidden state. The final hidden state of the encoder RNN, represented by \(\mathbf{c}\) then completely defines the encoding of the input sequence and is used as the initial hidden state of the decoder RNN. This can be seen as conditioning the decoder RNN on the encoded input.

To generate the first target vector, the decoder is fed the \(\text{BOS}\) vector, illustrated as \(\mathbf{y}_0\) in the design above. The target vector of the RNN is then further mapped to the logit vector \(\mathbf{l}_1\) by means of the LM Head feed-forward layer to define the conditional distribution of the first target vector as explained above:

$$ p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{c}). $$

The word \(\text{Ich}\) is sampled (shown by the grey arrow, connecting \(\mathbf{l}_1\) and \(\mathbf{y}_1\)) and consequently the second target vector can be sampled:

$$ \text{will} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \text{Ich}, \mathbf{c}). $$

And so on until at step \(i=6\), the \(\text{EOS}\) vector is sampled from \(\mathbf{l}6\) and the decoding is finished. The resulting target sequence amounts to \(\mathbf{Y}{1:6} = {\mathbf{y}_1, \ldots, \mathbf{y}_6}\), which is "Ich will ein Auto kaufen" in our example above.

To sum it up, an RNN-based encoder-decoder model, represented by \(f_{\theta_{\text{enc}}}\) and \( p_{\theta_{\text{dec}}} \) defines the distribution \(p(\mathbf{Y}{1:m} | \mathbf{X}{1:n})\) by factorization:

$$ p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}{1:m} | \mathbf{X}{1:n}) = \prod_{i=1}^{m} p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{X}{1:n}) = \prod{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{c}), \text{ with } \mathbf{c}=f_{\theta_{enc}}(X). $$

During inference, efficient decoding methods can auto-regressively generate the target sequence \(\mathbf{Y}_{1:m}\).

The RNN-based encoder-decoder model took the NLG community by storm. In 2016, Google announced to fully replace its heavily feature engineered translation service by a single RNN-based encoder-decoder model (see here).

Nevertheless, RNN-based encoder-decoder models have two pitfalls. First, RNNs suffer from the vanishing gradient problem, making it very difficult to capture long-range dependencies, cf. Hochreiter et al. (2001). Second, the inherent recurrent architecture of RNNs prevents efficient parallelization when encoding, cf. Vaswani et al. (2017).

---

\({}^1\) The original quote from the paper is "Despite their flexibility and power, DNNs can only be applied to problems whose inputs and targets can be sensibly encoded with vectors of fixed dimensionality", which is slightly adapted here.

\({}^2\) The same holds essentially true for convolutional neural networks (CNNs). While an input sequence of variable length can be fed into a CNN, the dimensionality of the target will always be dependent on the input dimensionality or fixed to a specific value.

\({}^3\) At the first step, the hidden state is initialized as a zero vector and fed to the RNN together with the first input vector \(\mathbf{x}_1\).

\({}^4\) A neural network can define a probability distribution over all words, i.e. \(p(\mathbf{y} | \mathbf{c}, \mathbf{Y}{0: i-1})\) as follows. First, the network defines a mapping from the inputs \(\mathbf{c}, \mathbf{Y}{0: i-1}\) to an embedded vector representation \(\mathbf{y'}\), which corresponds to the RNN target vector. The embedded vector representation \(\mathbf{y'}\) is then passed to the "language model head" layer, which means that it is multiplied by the word embedding matrix, i.e. \(\mathbf{Y}^{\text{vocab}}\), so that a score between \(\mathbf{y'}\) and each encoded vector \(\mathbf{y} \in \mathbf{Y}^{\text{vocab}}\) is computed. The resulting vector is called the logit vector \( \mathbf{l} = \mathbf{Y}^{\text{vocab}} \mathbf{y'} \) and can be mapped to a probability distribution over all words by applying a softmax operation: \(p(\mathbf{y} | \mathbf{c}) = \text{Softmax}(\mathbf{Y}^{\text{vocab}} \mathbf{y'}) = \text{Softmax}(\mathbf{l})\).

\({}^5\) Beam-search decoding is an example of such a decoding method. Different decoding methods are out of scope for this notebook. The reader is advised to refer to this interactive notebook on decoding methods.

\({}^6\) Sutskever et al. (2014) reverses the order of the input so that in the above example the input vectors would correspond to \(\mathbf{x}_1 = \text{car}\), \(\mathbf{x}_2 = \text{a}\), \(\mathbf{x}_3 = \text{buy}\), \(\mathbf{x}_4 = \text{to}\), \(\mathbf{x}_5 = \text{want}\), \(\mathbf{x}_6 = \text{I}\) and \(\mathbf{x}_7 = \text{EOS}\). The motivation is to allow for a shorter connection between corresponding word pairs such as \(\mathbf{x}_6 = \text{I}\) and \(\mathbf{y}_1 = \text{Ich}\). The research group emphasizes that the reversal of the input sequence was a key reason for their model's improved performance on machine translation.

Encoder-Decoder

In 2017, Vaswani et al. introduced the Transformer and thereby gave birth to transformer-based encoder-decoder models.

Analogous to RNN-based encoder-decoder models, transformer-based encoder-decoder models consist of an encoder and a decoder which are both stacks of residual attention blocks. The key innovation of transformer-based encoder-decoder models is that such residual attention blocks can process an input sequence \(\mathbf{X}_{1:n}\) of variable length \(n\) without exhibiting a recurrent structure. Not relying on a recurrent structure allows transformer-based encoder-decoders to be highly parallelizable, which makes the model orders of magnitude more computationally efficient than RNN-based encoder-decoder models on modern hardware.

As a reminder, to solve a sequence-to-sequence problem, we need to find a mapping of an input sequence \(\mathbf{X}{1:n}\) to an output sequence \(\mathbf{Y}{1:m}\) of variable length \(m\). Let's see how transformer-based encoder-decoder models are used to find such a mapping.

Similar to RNN-based encoder-decoder models, the transformer-based encoder-decoder models define a conditional distribution of target vectors \(\mathbf{Y}{1:n}\) given an input sequence \(\mathbf{X}{1:n}\):

$$ p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}{1:m} | \mathbf{X}{1:n}). $$

The transformer-based encoder part encodes the input sequence \(\mathbf{X}{1:n}\) to a sequence of hidden states \(\mathbf{\overline{X}}{1:n}\), thus defining the mapping:

$$ f_{\theta_{\text{enc}}}: \mathbf{X}{1:n} \to \mathbf{\overline{X}}{1:n}. $$

The transformer-based decoder part then models the conditional probability distribution of the target vector sequence \(\mathbf{Y}{1:n}\) given the sequence of encoded hidden states \(\mathbf{\overline{X}}{1:n}\):

$$ p_{\theta_{dec}}(\mathbf{Y}{1:n} | \mathbf{\overline{X}}{1:n}).$$

By Bayes' rule, this distribution can be factorized to a product of conditional probability distribution of the target vector \(\mathbf{y}i\) given the encoded hidden states \(\mathbf{\overline{X}}{1:n}\) and all previous target vectors \(\mathbf{Y}_{0:i-1}\):

$$ p_{\theta_{dec}}(\mathbf{Y}{1:n} | \mathbf{\overline{X}}{1:n}) = \prod_{i=1}^{n} p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n}). $$

The transformer-based decoder hereby maps the sequence of encoded hidden states \(\mathbf{\overline{X}}{1:n}\) and all previous target vectors \(\mathbf{Y}{0:i-1}\) to the logit vector \(\mathbf{l}i\). The logit vector \(\mathbf{l}i\) is then processed by the softmax operation to define the conditional distribution \(p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})\), just as it is done for RNN-based decoders. However, in contrast to RNN-based decoders, the distribution of the target vector \(\mathbf{y}_i\) is explicitly (or directly) conditioned on all previous target vectors \(\mathbf{y}0, \ldots, \mathbf{y}{i-1}\) as we will see later in more detail. The 0th target vector \(\mathbf{y}_0\) is hereby represented by a special "begin-of-sentence" \(\text{BOS}\) vector.

Having defined the conditional distribution \(p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}{1:n})\), we can now auto-regressively generate the output and thus define a mapping of an input sequence \(\mathbf{X}{1:n}\) to an output sequence \(\mathbf{Y}_{1:m}\) at inference.

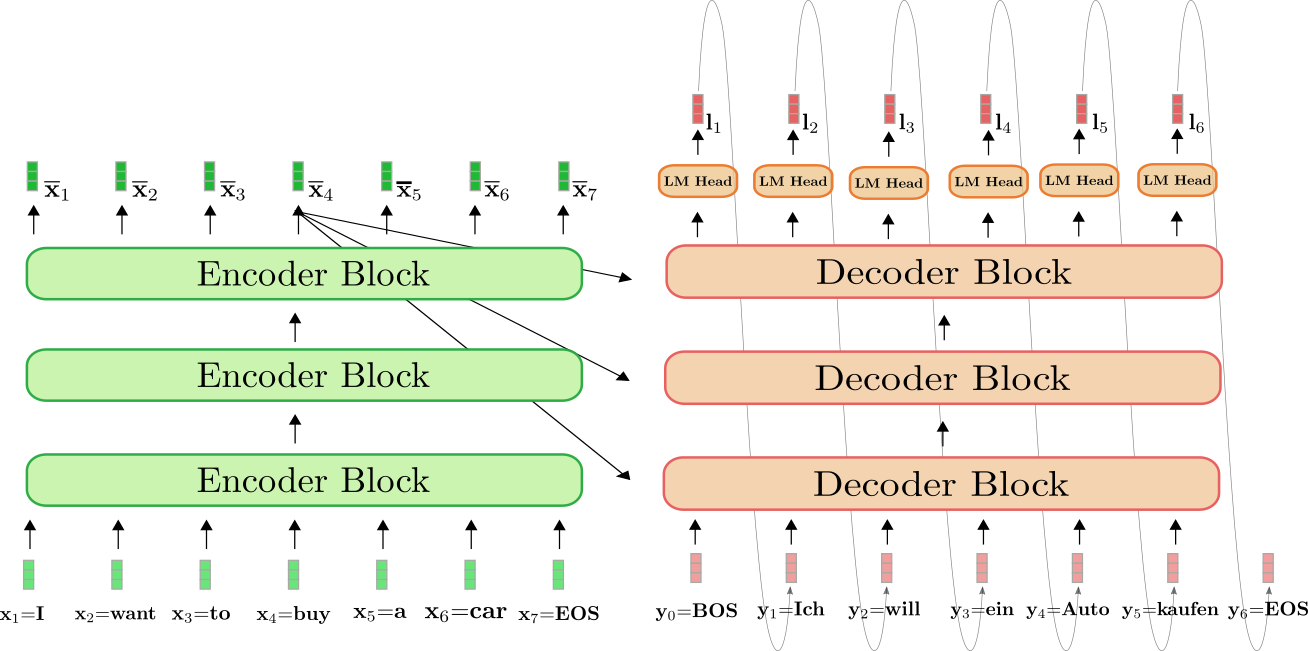
Let's visualize the complete process of auto-regressive generation of transformer-based encoder-decoder models.

The transformer-based encoder is colored in green and the transformer-based decoder is colored in red. As in the previous section, we show how the English sentence "I want to buy a car", represented by \(\mathbf{x}_1 = \text{I}\), \(\mathbf{x}_2 = \text{want}\), \(\mathbf{x}_3 = \text{to}\), \(\mathbf{x}_4 = \text{buy}\), \(\mathbf{x}_5 = \text{a}\), \(\mathbf{x}_6 = \text{car}\), and \(\mathbf{x}_7 = \text{EOS}\) is translated into German: "Ich will ein Auto kaufen" defined as \(\mathbf{y}_0 = \text{BOS}\), \(\mathbf{y}_1 = \text{Ich}\), \(\mathbf{y}_2 = \text{will}\), \(\mathbf{y}_3 = \text{ein}\), \(\mathbf{y}_4 = \text{Auto}, \mathbf{y}_5 = \text{kaufen}\), and \(\mathbf{y}_6=\text{EOS}\).

To begin with, the encoder processes the complete input sequence \(\mathbf{X}{1:7}\) = "I want to buy a car" (represented by the light green vectors) to a contextualized encoded sequence \(\mathbf{\overline{X}}{1:7}\). E.g. \(\mathbf{\overline{x}}_4\) defines an encoding that depends not only on the input \(\mathbf{x}_4\) = "buy", but also on all other words "I", "want", "to", "a", "car" and "EOS", i.e. the context.

Next, the input encoding \(\mathbf{\overline{X}}_{1:7}\) together with the BOS vector, i.e. \(\mathbf{y}0\), is fed to the decoder. The decoder processes the inputs \(\mathbf{\overline{X}}{1:7}\) and \(\mathbf{y}_0\) to the first logit \(\mathbf{l}_1\) (shown in darker red) to define the conditional distribution of the first target vector \(\mathbf{y}_1\):

$$ p_{\theta_{enc, dec}}(\mathbf{y} | \mathbf{y}0, \mathbf{X}{1:7}) = p_{\theta_{enc, dec}}(\mathbf{y} | \text{BOS}, \text{I want to buy a car EOS}) = p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7}). $$

Next, the first target vector \(\mathbf{y}_1\) = \(\text{Ich}\) is sampled from the distribution (represented by the grey arrows) and can now be fed to the decoder again. The decoder now processes both \(\mathbf{y}_0\) = "BOS" and \(\mathbf{y}_1\) = "Ich" to define the conditional distribution of the second target vector \(\mathbf{y}_2\):

$$ p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7}). $$

We can sample again and produce the target vector \(\mathbf{y}_2\) = "will". We continue in auto-regressive fashion until at step 6 the EOS vector is sampled from the conditional distribution:

$$ \text{EOS} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}). $$

And so on in auto-regressive fashion.

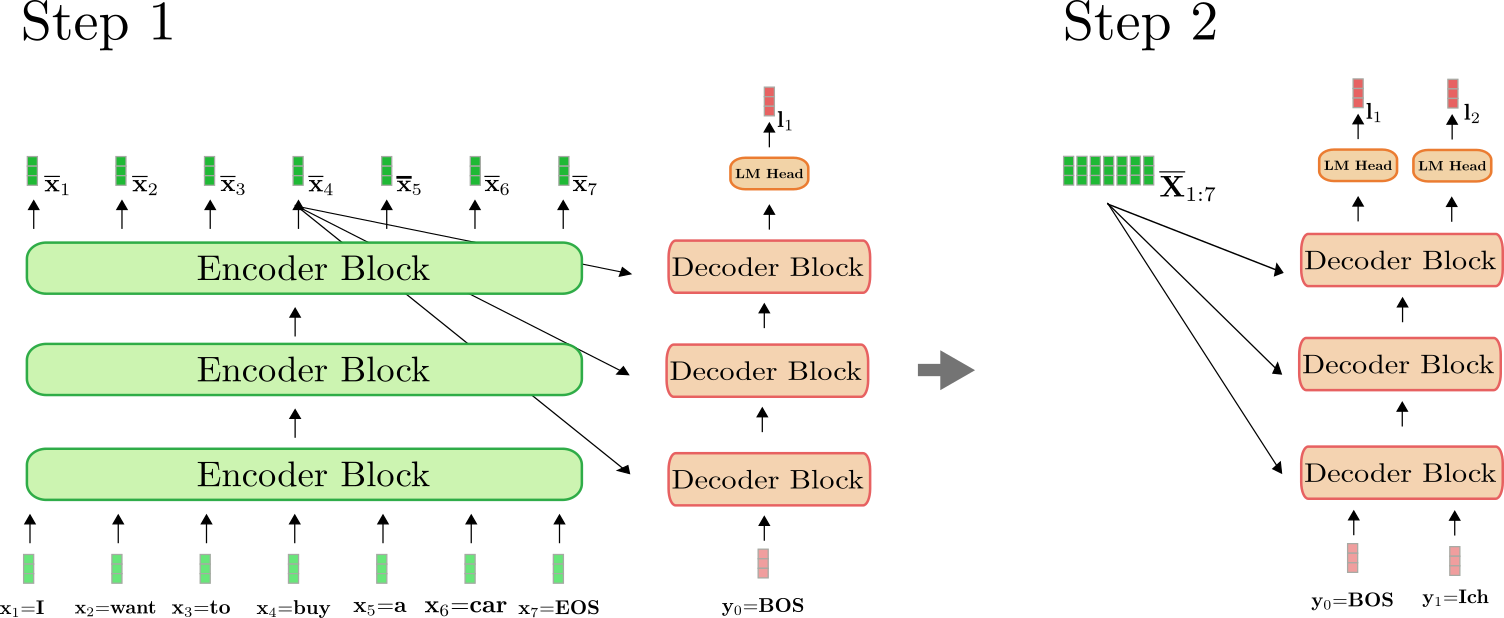
It is important to understand that the encoder is only used in the first forward pass to map \(\mathbf{X}{1:n}\) to \(\mathbf{\overline{X}}{1:n}\). As of the second forward pass, the decoder can directly make use of the previously calculated encoding \(\mathbf{\overline{X}}_{1:n}\). For clarity, let's illustrate the first and the second forward pass for our example above.

As can be seen, only in step \(i=1\) do we have to encode "I want to buy a car EOS" to \(\mathbf{\overline{X}}_{1:7}\). At step \(i=2\), the contextualized encodings of "I want to buy a car EOS" are simply reused by the decoder.

In 🤗Transformers, this auto-regressive generation is done under-the-hood when calling the .generate() method. Let's use one of our translation models to see this in action.

from transformers import MarianMTModel, MarianTokenizer

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# translate example
output_ids = model.generate(input_ids)[0]

# decode and print
print(tokenizer.decode(output_ids))

Output:

    <pad> Ich will ein Auto kaufen

Calling .generate() does many things under-the-hood. First, it passes the input_ids to the encoder. Second, it passes a pre-defined token, which is the \(\text{}\) symbol in the case of MarianMTModel along with the encoded input_ids to the decoder. Third, it applies the beam search decoding mechanism to auto-regressively sample the next output word of the last decoder output \({}^1\). For more detail on how beam search decoding works, one is advised to read this blog post.

In the Appendix, we have included a code snippet that shows how a simple generation method can be implemented "from scratch". To fully understand how auto-regressive generation works under-the-hood, it is highly recommended to read the Appendix.

To sum it up:

• The transformer-based encoder defines a mapping from the input sequence \(\mathbf{X}{1:n}\) to a contextualized encoding sequence \(\mathbf{\overline{X}}{1:n}\).
• The transformer-based decoder defines the conditional distribution \(p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})\).
• Given an appropriate decoding mechanism, the output sequence \(\mathbf{Y}{1:m}\) can auto-regressively be sampled from \(p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in {1, \ldots, m}\).

Great, now that we have gotten a general overview of how transformer-based encoder-decoder models work, we can dive deeper into both the encoder and decoder part of the model. More specifically, we will see exactly how the encoder makes use of the self-attention layer to yield a sequence of context-dependent vector encodings and how self-attention layers allow for efficient parallelization. Then, we will explain in detail how the self-attention layer works in the decoder model and how the decoder is conditioned on the encoder's output with cross-attention layers to define the conditional distribution \(p_{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})\). Along, the way it will become obvious how transformer-based encoder-decoder models solve the long-range dependencies problem of RNN-based encoder-decoder models.

---

\({}^1\) In the case of "Helsinki-NLP/opus-mt-en-de", the decoding parameters can be accessed here, where we can see that model applies beam search with num_beams=6.

Encoder

As mentioned in the previous section, the transformer-based encoder maps the input sequence to a contextualized encoding sequence:

$$ f_{\theta_{\text{enc}}}: \mathbf{X}{1:n} \to \mathbf{\overline{X}}{1:n}. $$

Taking a closer look at the architecture, the transformer-based encoder is a stack of residual encoder blocks. Each encoder block consists of a bi-directional self-attention layer, followed by two feed-forward layers. For simplicity, we disregard the normalization layers in this notebook. Also, we will not further discuss the role of the two feed-forward layers, but simply see it as a final vector-to-vector mapping required in each encoder block \({}^1\). The bi-directional self-attention layer puts each input vector \(\mathbf{x'}_j, \forall j \in {1, \ldots, n}\) into relation with all input vectors \(\mathbf{x'}_1, \ldots, \mathbf{x'}_n\) and by doing so transforms the input vector \(\mathbf{x'}j\) to a more "refined" contextual representation of itself, defined as \(\mathbf{x''}j\). Thereby, the first encoder block transforms each input vector of the input sequence \(\mathbf{X}{1:n}\) (shown in light green below) from a context-independent vector representation to a context-dependent vector representation, and the following encoder blocks further refine this contextual representation until the last encoder block outputs the final contextual encoding \(\mathbf{\overline{X}}{1:n}\) (shown in darker green below).

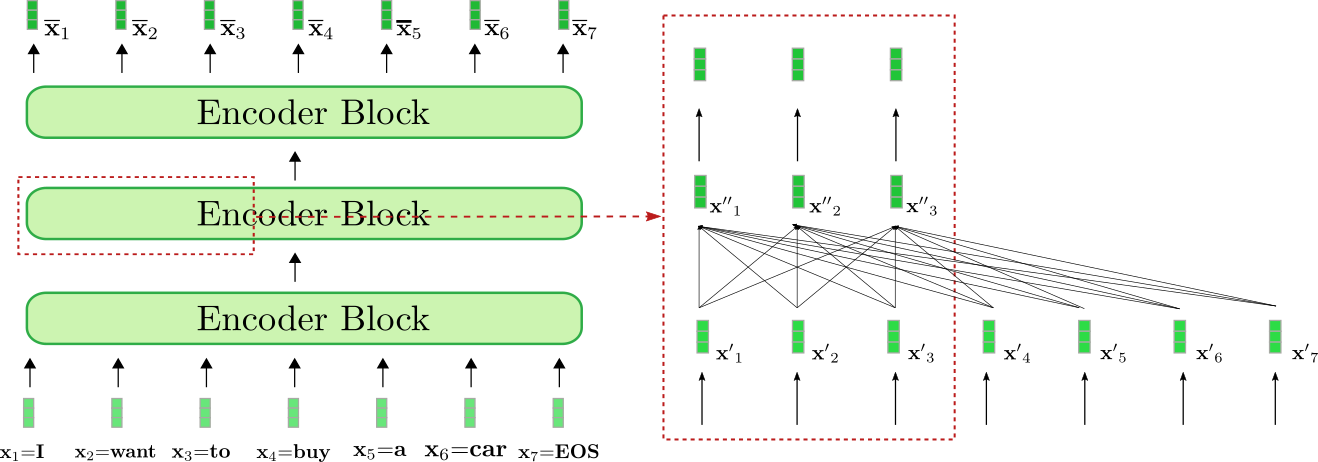
Let's visualize how the encoder processes the input sequence "I want to buy a car EOS" to a contextualized encoding sequence. Similar to RNN-based encoders, transformer-based encoders also add a special "end-of-sequence" input vector to the input sequence to hint to the model that the input vector sequence is finished \({}^2\).

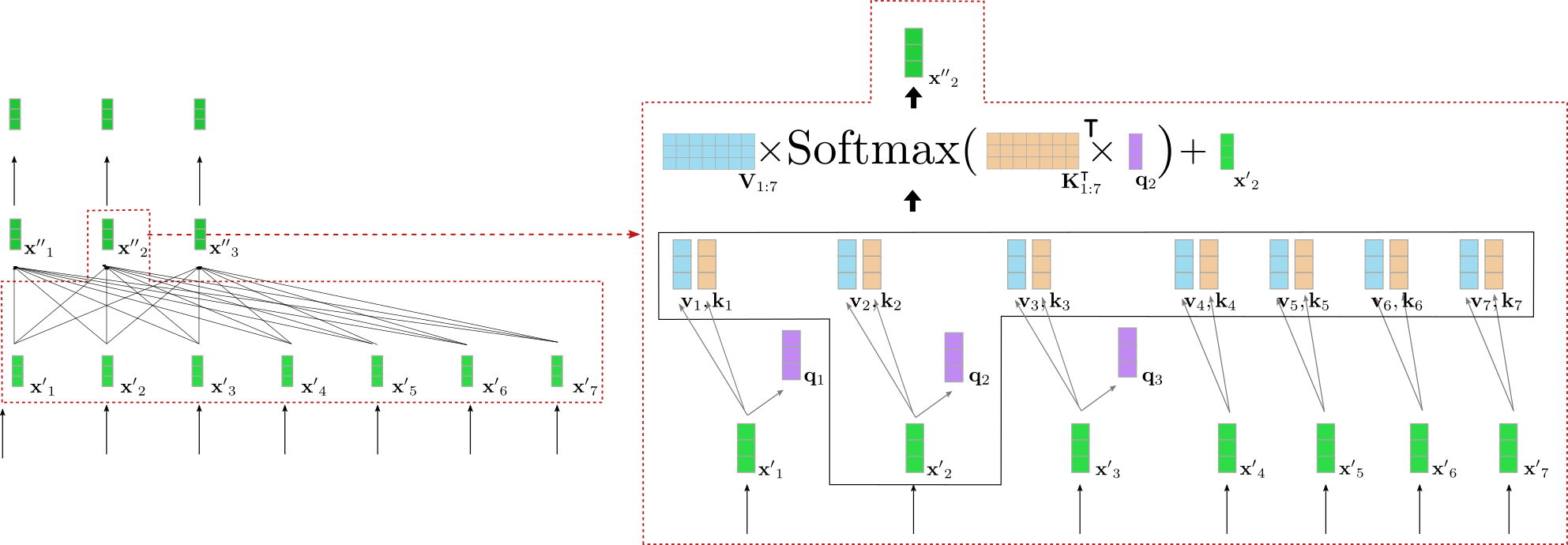
Our exemplary transformer-based encoder is composed of three encoder blocks, whereas the second encoder block is shown in more detail in the red box on the right for the first three input vectors \(\mathbf{x}_1, \mathbf{x}_2 and \mathbf{x}_3\). The bi-directional self-attention mechanism is illustrated by the fully-connected graph in the lower part of the red box and the two feed-forward layers are shown in the upper part of the red box. As stated before, we will focus only on the bi-directional self-attention mechanism.

As can be seen each output vector of the self-attention layer \(\mathbf{x''}_i, \forall i \in {1, \ldots, 7}\) depends directly on all input vectors \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\). This means, e.g. that the input vector representation of the word "want", i.e. \(\mathbf{x'}_2\), is put into direct relation with the word "buy", i.e. \(\mathbf{x'}_4\), but also with the word "I",i.e. \(\mathbf{x'}_1\). The output vector representation of "want", i.e. \(\mathbf{x''}_2\), thus represents a more refined contextual representation for the word "want".

Let's take a deeper look at how bi-directional self-attention works. Each input vector \(\mathbf{x'}i\) of an input sequence \(\mathbf{X'}{1:n}\) of an encoder block is projected to a key vector \(\mathbf{k}_i\), value vector \(\mathbf{v}_i\) and query vector \(\mathbf{q}_i\) (shown in orange, blue, and purple respectively below) through three trainable weight matrices \(\mathbf{W}_q, \mathbf{W}_v, \mathbf{W}_k\):

$$ \mathbf{q}_i = \mathbf{W}_q \mathbf{x'}_i,$$ $$ \mathbf{v}_i = \mathbf{W}_v \mathbf{x'}_i,$$ $$ \mathbf{k}_i = \mathbf{W}_k \mathbf{x'}_i, $$ $$ \forall i \in {1, \ldots n }.$$

Note, that the same weight matrices are applied to each input vector \(\mathbf{x}_i, \forall i \in {i, \ldots, n}\). After projecting each input vector \(\mathbf{x}_i\) to a query, key, and value vector, each query vector \(\mathbf{q}_j, \forall j \in {1, \ldots, n}\) is compared to all key vectors \(\mathbf{k}_1, \ldots, \mathbf{k}_n\). The more similar one of the key vectors \(\mathbf{k}_1, \ldots \mathbf{k}_n\) is to a query vector \(\mathbf{q}_j\), the more important is the corresponding value vector \(\mathbf{v}_j\) for the output vector \(\mathbf{x''}_j\). More specifically, an output vector \(\mathbf{x''}_j\) is defined as the weighted sum of all value vectors \(\mathbf{v}_1, \ldots, \mathbf{v}_n\) plus the input vector \(\mathbf{x'}_j\). Thereby, the weights are proportional to the cosine similarity between \(\mathbf{q}_j\) and the respective key vectors \(\mathbf{k}_1, \ldots, \mathbf{k}n\), which is mathematically expressed by \(\textbf{Softmax}(\mathbf{K}{1:n}^\intercal \mathbf{q}_j)\) as illustrated in the equation below. For a complete description of the self-attention layer, the reader is advised to take a look at this blog post or the original paper.

Alright, this sounds quite complicated. Let's illustrate the bi-directional self-attention layer for one of the query vectors of our example above. For simplicity, it is assumed that our exemplary transformer-based decoder uses only a single attention head config.num_heads = 1 and that no normalization is applied.

On the left, the previously illustrated second encoder block is shown again and on the right, an in detail visualization of the bi-directional self-attention mechanism is given for the second input vector \(\mathbf{x'}_2\) that corresponds to the input word "want". At first all input vectors \(\mathbf{x'}_1, \ldots, \mathbf{x'}_7\) are projected to their respective query vectors \(\mathbf{q}_1, \ldots, \mathbf{q}_7\) (only the first three query vectors are shown in purple above), value vectors \(\mathbf{v}_1, \ldots, \mathbf{v}_7\) (shown in blue), and key vectors \(\mathbf{k}_1, \ldots, \mathbf{k}_7\) (shown in orange). The query vector \(\mathbf{q}2\) is then multiplied by the transpose of all key vectors, i.e. \(\mathbf{K}{1:7}^{\intercal}\) followed by the softmax operation to yield the self-attention weights. The self-attention weights are finally multiplied by the respective value vectors and the input vector \(\mathbf{x'}_2\) is added to output the "refined" representation of the word "want", i.e. \(\mathbf{x''}2\) (shown in dark green on the right). The whole equation is illustrated in the upper part of the box on the right. The multiplication of \(\mathbf{K}{1:7}^{\intercal}\) and \(\mathbf{q}_2\) thereby makes it possible to compare the vector representation of "want" to all other input vector representations "I", "to", "buy", "a", "car", "EOS" so that the self-attention weights mirror the importance each of the other input vector representations \(\mathbf{x'}_j \text{, with } j \ne 2\) for the refined representation \(\mathbf{x''}_2\) of the word "want".

To further understand the implications of the bi-directional self-attention layer, let's assume the following sentence is processed: "The house is beautiful and well located in the middle of the city where it is easily accessible by public transport". The word "it" refers to "house", which is 12 "positions away". In transformer-based encoders, the bi-directional self-attention layer performs a single mathematical operation to put the input vector of "house" into relation with the input vector of "it" (compare to the first illustration of this section). In contrast, in an RNN-based encoder, a word that is 12 "positions away", would require at least 12 mathematical operations meaning that in an RNN-based encoder a linear number of mathematical operations are required. This makes it much harder for an RNN-based encoder to model long-range contextual representations. Also, it becomes clear that a transformer-based encoder is much less prone to lose important information than an RNN-based encoder-decoder model because the sequence length of the encoding is kept the same, i.e. \(\textbf{len}(\mathbf{X}{1:n}) = \textbf{len}(\mathbf{\overline{X}}{1:n}) = n\), while an RNN compresses the length from \(*\textbf{len}((\mathbf{X}_{1:n}) = n\) to just \(\textbf{len}(\mathbf{c}) = 1\), which makes it very difficult for RNNs to effectively encode long-range dependencies between input words.

In addition to making long-range dependencies more easily learnable, we can see that the Transformer architecture is able to process text in parallel.Mathematically, this can easily be shown by writing the self-attention formula as a product of query, key, and value matrices:

$$\mathbf{X''}{1:n} = \mathbf{V}{1:n} \text{Softmax}(\mathbf{Q}{1:n}^\intercal \mathbf{K}{1:n}) + \mathbf{X'}_{1:n}. $$

The output \(\mathbf{X''}_{1:n} = \mathbf{x''}_1, \ldots, \mathbf{x''}_n\) is computed via a series of matrix multiplications and a softmax operation, which can be parallelized effectively. Note, that in an RNN-based encoder model, the computation of the hidden state \(\mathbf{c}\) has to be done sequentially: Compute hidden state of the first input vector \(\mathbf{x}_1\), then compute the hidden state of the second input vector that depends on the hidden state of the first hidden vector, etc. The sequential nature of RNNs prevents effective parallelization and makes them much more inefficient compared to transformer-based encoder models on modern GPU hardware.

Great, now we should have a better understanding of a) how transformer-based encoder models effectively model long-range contextual representations and b) how they efficiently process long sequences of input vectors.

Now, let's code up a short example of the encoder part of our MarianMT encoder-decoder models to verify that the explained theory holds in practice.

---

\({}^1\) An in-detail explanation of the role the feed-forward layers play in transformer-based models is out-of-scope for this notebook. It is argued in Yun et. al, (2017) that feed-forward layers are crucial to map each contextual vector \(\mathbf{x'}_i\) individually to the desired output space, which the self-attention layer does not manage to do on its own. It should be noted here, that each output token \(\mathbf{x'}\) is processed by the same feed-forward layer. For more detail, the reader is advised to read the paper.

\({}^2\) However, the EOS input vector does not have to be appended to the input sequence, but has been shown to improve performance in many cases. In contrast to the 0th \(\text{BOS}\) target vector of the transformer-based decoder is required as a starting input vector to predict a first target vector.

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

embeddings = model.get_input_embeddings()

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state

# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))

Outputs:

    Length of input embeddings 7. Length of encoder_hidden_states 7
    Is encoding for `I` equal to its perturbed version?:  False

We compare the length of the input word embeddings, i.e. embeddings(input_ids) corresponding to \(\mathbf{X}{1:n}\), with the length of the encoder_hidden_states, corresponding to \(\mathbf{\overline{X}}{1:n}\). Also, we have forwarded the word sequence "I want to buy a car" and a slightly perturbated version "I want to buy a house" through the encoder to check if the first output encoding, corresponding to "I", differs when only the last word is changed in the input sequence.

As expected the output length of the input word embeddings and encoder output encodings, i.e. \(\textbf{len}(\mathbf{X}{1:n})\) and \(\textbf{len}(\mathbf{\overline{X}}{1:n})\), is equal. Second, it can be noted that the values of the encoded output vector of \(\mathbf{\overline{x}}_1 = \text{"I"}\) are different when the last word is changed from "car" to "house". This however should not come as a surprise if one has understood bi-directional self-attention.

On a side-note, autoencoding models, such as BERT, have the exact same architecture as transformer-based encoder models. Autoencoding models leverage this architecture for massive self-supervised pre-training on open-domain text data so that they can map any word sequence to a deep bi-directional representation. In Devlin et al. (2018), the authors show that a pre-trained BERT model with a single task-specific classification layer on top can achieve SOTA results on eleven NLP tasks. All autoencoding models of 🤗Transformers can be found here.

Decoder

As mentioned in the Encoder-Decoder section, the transformer-based decoder defines the conditional probability distribution of a target sequence given the contextualized encoding sequence:

$$ p_{\theta_{dec}}(\mathbf{Y}{1: m} | \mathbf{\overline{X}}{1:n}), $$

which by Bayes' rule can be decomposed into a product of conditional distributions of the next target vector given the contextualized encoding sequence and all previous target vectors:

$$ p_{\theta_{dec}}(\mathbf{Y}{1:m} | \mathbf{\overline{X}}{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n}). $$

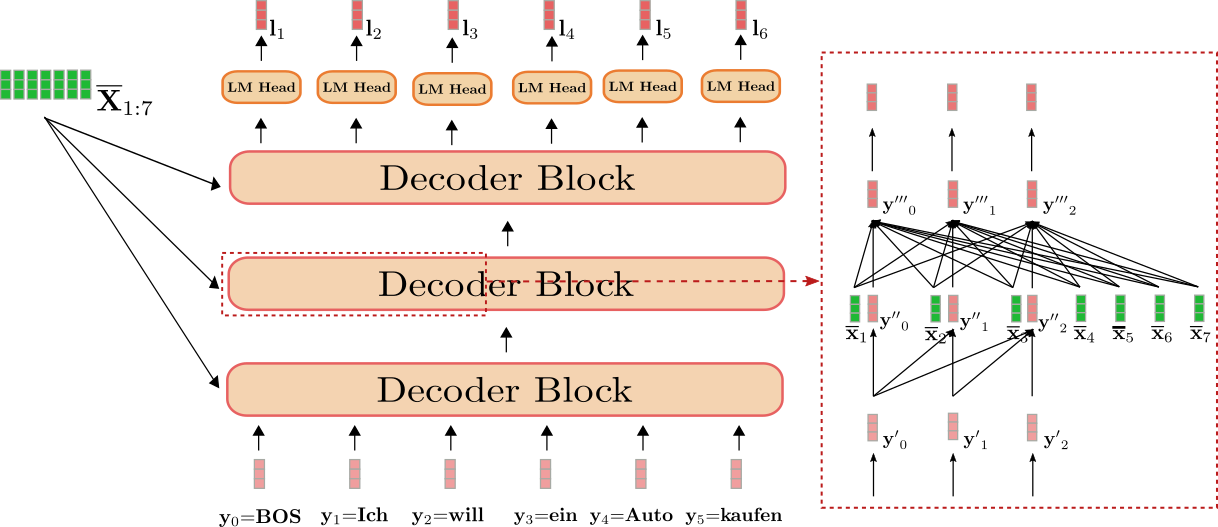
Let's first understand how the transformer-based decoder defines a probability distribution. The transformer-based decoder is a stack of decoder blocks followed by a dense layer, the "LM head". The stack of decoder blocks maps the contextualized encoding sequence \(\mathbf{\overline{X}}{1:n}\) and a target vector sequence prepended by the \(\text{BOS}\) vector and cut to the last target vector, i.e. \(\mathbf{Y}{0:i-1}\), to an encoded sequence of target vectors \(\mathbf{\overline{Y}}{0: i-1}\). Then, the "LM head" maps the encoded sequence of target vectors \(\mathbf{\overline{Y}}{0: i-1}\) to a sequence of logit vectors \(\mathbf{L}_{1:n} = \mathbf{l}_1, \ldots, \mathbf{l}_n\), whereas the dimensionality of each logit vector \(\mathbf{l}_i\) corresponds to the size of the vocabulary. This way, for each \(i \in {1, \ldots, n}\) a probability distribution over the whole vocabulary can be obtained by applying a softmax operation on \(\mathbf{l}_i\). These distributions define the conditional distribution:

$$p_{\theta_{dec}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in {1, \ldots, n},$$

respectively. The "LM head" is often tied to the transpose of the word embedding matrix, i.e. \(\mathbf{W}_{\text{emb}}^{\intercal} = \left[\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}\right]^{\intercal}\) \({}^1\). Intuitively this means that for all \(i \in {0, \ldots, n - 1}\) the "LM Head" layer compares the encoded output vector \(\mathbf{\overline{y}}i\) to all word embeddings in the vocabulary \(\mathbf{y}^1, \ldots, \mathbf{y}^{\text{vocab}}\) so that the logit vector \(\mathbf{l}{i+1}\) represents the similarity scores between the encoded output vector and each word embedding. The softmax operation simply transformers the similarity scores to a probability distribution. For each \(i \in {1, \ldots, n}\), the following equations hold:

$$ p_{\theta_{dec}}(\mathbf{y} | \mathbf{\overline{X}}{1:n}, \mathbf{Y}{0:i-1})$$ $$ = \text{Softmax}(f_{\theta_{\text{dec}}}(\mathbf{\overline{X}}{1:n}, \mathbf{Y}{0:i-1}))$$ $$ = \text{Softmax}(\mathbf{W}{\text{emb}}^{\intercal} \mathbf{\overline{y}}{i-1})$$ $$ = \text{Softmax}(\mathbf{l}_i). $$

Putting it all together, in order to model the conditional distribution of a target vector sequence \(\mathbf{Y}{1: m}\), the target vectors \(\mathbf{Y}{1:m-1}\) prepended by the special \(\text{BOS}\) vector, i.e. \(\mathbf{y}0\), are first mapped together with the contextualized encoding sequence \(\mathbf{\overline{X}}{1:n}\) to the logit vector sequence \(\mathbf{L}_{1:m}\). Consequently, each logit target vector \(\mathbf{l}_i\) is transformed into a conditional probability distribution of the target vector \(\mathbf{y}_i\) using the softmax operation. Finally, the conditional probabilities of all target vectors \(\mathbf{y}_1, \ldots, \mathbf{y}_m\) multiplied together to yield the conditional probability of the complete target vector sequence:

$$ p_{\theta_{dec}}(\mathbf{Y}{1:m} | \mathbf{\overline{X}}{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n}).$$

In contrast to transformer-based encoders, in transformer-based decoders, the encoded output vector \(\mathbf{\overline{y}}i\) should be a good representation of the next target vector \(\mathbf{y}{i+1}\) and not of the input vector itself. Additionally, the encoded output vector \(\mathbf{\overline{y}}i\) should be conditioned on all contextualized encoding sequence \(\mathbf{\overline{X}}{1:n}\). To meet these requirements each decoder block consists of a uni-directional self-attention layer, followed by a cross-attention layer and two feed-forward layers \({}^2\). The uni-directional self-attention layer puts each of its input vectors \(\mathbf{y'}_j\) only into relation with all previous input vectors \(\mathbf{y'}_i, \text{ with } i \le j\) for all \(j \in {1, \ldots, n}\) to model the probability distribution of the next target vectors. The cross-attention layer puts each of its input vectors \(\mathbf{y''}j\) into relation with all contextualized encoding vectors \(\mathbf{\overline{X}}{1:n}\) to condition the probability distribution of the next target vectors on the input of the encoder as well.

Alright, let's visualize the transformer-based decoder for our English to German translation example.

We can see that the decoder maps the input \(\mathbf{Y}{0:5}\) "BOS", "Ich", "will", "ein", "Auto", "kaufen" (shown in light red) together with the contextualized sequence of "I", "want", "to", "buy", "a", "car", "EOS", i.e. \(\mathbf{\overline{X}}{1:7}\) (shown in dark green) to the logit vectors \(\mathbf{L}_{1:6}\) (shown in dark red).

Applying a softmax operation on each \(\mathbf{l}_1, \mathbf{l}_2, \ldots, \mathbf{l}_5\) can thus define the conditional probability distributions:

$$ p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}{1:7}), $$ $$ p{\theta_{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}{1:7}), $$ $$ \ldots, $$ $$ p{\theta_{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}). $$

The overall conditional probability of:

$$ p_{\theta_{dec}}(\text{Ich will ein Auto kaufen EOS} | \mathbf{\overline{X}}_{1:n})$$

can therefore be computed as the following product:

$$ p_{\theta_{dec}}(\text{Ich} | \text{BOS}, \mathbf{\overline{X}}{1:7}) \times \ldots \times p{\theta_{dec}}(\text{EOS} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}). $$

The red box on the right shows a decoder block for the first three target vectors \(\mathbf{y}_0, \mathbf{y}_1, \mathbf{y}_2\). In the lower part, the uni-directional self-attention mechanism is illustrated and in the middle, the cross-attention mechanism is illustrated. Let's first focus on uni-directional self-attention.

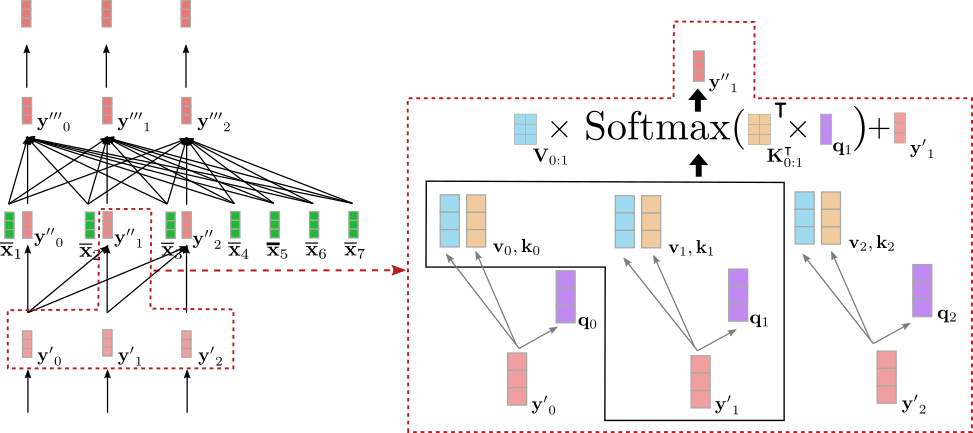
As in bi-directional self-attention, in uni-directional self-attention, the query vectors \(\mathbf{q}0, \ldots, \mathbf{q}{m-1}\) (shown in purple below), key vectors \(\mathbf{k}0, \ldots, \mathbf{k}{m-1}\) (shown in orange below), and value vectors \(\mathbf{v}0, \ldots, \mathbf{v}{m-1}\) (shown in blue below) are projected from their respective input vectors \(\mathbf{y'}0, \ldots, \mathbf{y'}{m-1}\) (shown in light red below). However, in uni-directional self-attention, each query vector \(\mathbf{q}_i\) is compared only to its respective key vector and all previous ones, namely \(\mathbf{k}_0, \ldots, \mathbf{k}_i\) to yield the respective attention weights. This prevents an output vector \(\mathbf{y''}_j\) (shown in dark red below) to include any information about the following input vector \(\mathbf{y}_i, \text{ with } i > j\) for all \(j \in {0, \ldots, m - 1 }\). As is the case in bi-directional self-attention, the attention weights are then multiplied by their respective value vectors and summed together.

We can summarize uni-directional self-attention as follows:

$$\mathbf{y''}i = \mathbf{V}{0: i} \textbf{Softmax}(\mathbf{K}_{0: i}^\intercal \mathbf{q}_i) + \mathbf{y'}_i. $$

Note that the index range of the key and value vectors is \(0:i\) instead of \(0: m-1\) which would be the range of the key vectors in bi-directional self-attention.

Let's illustrate uni-directional self-attention for the input vector \(\mathbf{y'}_1\) for our example above.

As can be seen \(\mathbf{y''}_1\) only depends on \(\mathbf{y'}_0\) and \(\mathbf{y'}_1\). Therefore, we put the vector representation of the word "Ich", i.e. \(\mathbf{y'}_1\) only into relation with itself and the "BOS" target vector, i.e. \(\mathbf{y'}_0\), but not with the vector representation of the word "will", i.e. \(\mathbf{y'}_2\).

So why is it important that we use uni-directional self-attention in the decoder instead of bi-directional self-attention? As stated above, a transformer-based decoder defines a mapping from a sequence of input vector \(\mathbf{Y}{0: m-1}\) to the logits corresponding to the next decoder input vectors, namely \(\mathbf{L}{1:m}\). In our example, this means, e.g. that the input vector \(\mathbf{y}_1\) = "Ich" is mapped to the logit vector \(\mathbf{l}_2\), which is then used to predict the input vector \(\mathbf{y}_2\). Thus, if \(\mathbf{y'}1\) would have access to the following input vectors \(\mathbf{Y'}{2:5}\), the decoder would simply copy the vector representation of "will", i.e. \(\mathbf{y'}_2\), to be its output \(\mathbf{y''}_1\). This would be forwarded to the last layer so that the encoded output vector \(\mathbf{\overline{y}}_1\) would essentially just correspond to the vector representation \(\mathbf{y}_2\).

This is obviously disadvantageous as the transformer-based decoder would never learn to predict the next word given all previous words, but just copy the target vector \(\mathbf{y}i\) through the network to \(\mathbf{\overline{y}}{i-1}\) for all \(i \in {1, \ldots, m }\). In order to define a conditional distribution of the next target vector, the distribution cannot be conditioned on the next target vector itself. It does not make much sense to predict \(\mathbf{y}i\) from \(p(\mathbf{y} | \mathbf{Y}{0:i}, \mathbf{\overline{X}})\) because the distribution is conditioned on the target vector it is supposed to model. The uni-directional self-attention architecture, therefore, allows us to define a causal probability distribution, which is necessary to effectively model a conditional distribution of the next target vector.

Great! Now we can move to the layer that connects the encoder and decoder - the cross-attention mechanism!

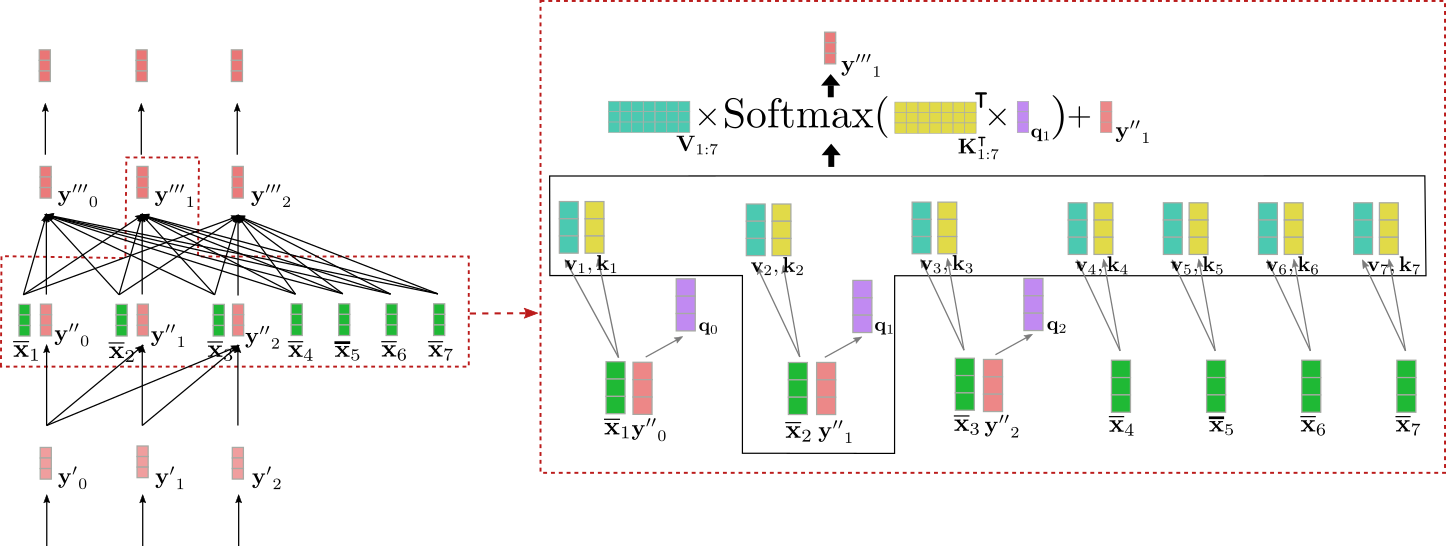
The cross-attention layer takes two vector sequences as inputs: the outputs of the uni-directional self-attention layer, i.e. \(\mathbf{Y''}{0: m-1}\) and the contextualized encoding vectors \(\mathbf{\overline{X}}{1:n}\). As in the self-attention layer, the query vectors \(\mathbf{q}0, \ldots, \mathbf{q}{m-1}\) are projections of the output vectors of the previous layer, i.e. \(\mathbf{Y''}{0: m-1}\). However, the key and value vectors \(\mathbf{k}0, \ldots, \mathbf{k}{m-1}\) and \(\mathbf{v}0, \ldots, \mathbf{v}{m-1}\) are projections of the contextualized encoding vectors \(\mathbf{\overline{X}}{1:n}\). Having defined key, value, and query vectors, a query vector \(\mathbf{q}_i\) is then compared to all key vectors and the corresponding score is used to weight the respective value vectors, just as is the case for bi-directional self-attention to give the output vector \(\mathbf{y'''}_i\) for all \(i \in {0, \ldots, m-1}\). Cross-attention can be summarized as follows:

$$ \mathbf{y'''}i = \mathbf{V}{1:n} \textbf{Softmax}(\mathbf{K}_{1: n}^\intercal \mathbf{q}_i) + \mathbf{y''}_i. $$

Note that the index range of the key and value vectors is \(1:n\) corresponding to the number of contextualized encoding vectors.

Let's visualize the cross-attention mechanism Let's for the input vector \(\mathbf{y''}_1\) for our example above.

We can see that the query vector \(\mathbf{q}_1\) (shown in purple) is derived from \(\mathbf{y''}_1\)(shown in red) and therefore relies on a vector representation of the word "Ich". The query vector \(\mathbf{q}_1\) is then compared to the key vectors \(\mathbf{k}_1, \ldots, \mathbf{k}7\) (shown in yellow) corresponding to the contextual encoding representation of all encoder input vectors \(\mathbf{X}{1:n}\) = "I want to buy a car EOS". This puts the vector representation of "Ich" into direct relation with all encoder input vectors. Finally, the attention weights are multiplied by the value vectors \(\mathbf{v}_1, \ldots, \mathbf{v}_7\) (shown in turquoise) to yield in addition to the input vector \(\mathbf{y''}_1\) the output vector \(\mathbf{y'''}_1\) (shown in dark red).

So intuitively, what happens here exactly? Each output vector \(\mathbf{y'''}i\) is a weighted sum of all value projections of the encoder inputs \(\mathbf{v}{1}, \ldots, \mathbf{v}_7\) plus the input vector itself \(\mathbf{y''}_i\) (c.f. illustrated formula above). The key mechanism to understand is the following: Depending on how similar a query projection of the input decoder vector \(\mathbf{q}_i\) is to a key projection of the encoder input vector \(\mathbf{k}_j\), the more important is the value projection of the encoder input vector \(\mathbf{v}_j\). In loose terms this means, the more "related" a decoder input representation is to an encoder input representation, the more does the input representation influence the decoder output representation.

Cool! Now we can see how this architecture nicely conditions each output vector \(\mathbf{y'''}i\) on the interaction between the encoder input vectors \(\mathbf{\overline{X}}{1:n}\) and the input vector \(\mathbf{y''}i\). Another important observation at this point is that the architecture is completely independent of the number \(n\) of contextualized encoding vectors \(\mathbf{\overline{X}}{1:n}\) on which the output vector \(\mathbf{y'''}i\) is conditioned on. All projection matrices \(\mathbf{W}^{\text{cross}}{k}\) and \(\mathbf{W}^{\text{cross}}_{v}\) to derive the key vectors \(\mathbf{k}_1, \ldots, \mathbf{k}_n\) and the value vectors \(\mathbf{v}_1, \ldots, \mathbf{v}_n\) respectively are shared across all positions \(1, \ldots, n\) and all value vectors \( \mathbf{v}_1, \ldots, \mathbf{v}_n \) are summed together to a single weighted averaged vector. Now it becomes obvious as well, why the transformer-based decoder does not suffer from the long-range dependency problem, the RNN-based decoder suffers from. Because each decoder logit vector is directly dependent on every single encoded output vector, the number of mathematical operations to compare the first encoded output vector and the last decoder logit vector amounts essentially to just one.

To conclude, the uni-directional self-attention layer is responsible for conditioning each output vector on all previous decoder input vectors and the current input vector and the cross-attention layer is responsible to further condition each output vector on all encoded input vectors.

To verify our theoretical understanding, let's continue our code example from the encoder section above.

---

\({}^1\) The word embedding matrix \(\mathbf{W}_{\text{emb}}\) gives each input word a unique context-independent vector representation. This matrix is often fixed as the "LM Head" layer. However, the "LM Head" layer can very well consist of a completely independent "encoded vector-to-logit" weight mapping.

\({}^2\) Again, an in-detail explanation of the role the feed-forward layers play in transformer-based models is out-of-scope for this notebook. It is argued in Yun et. al, (2017) that feed-forward layers are crucial to map each contextual vector \(\mathbf{x'}_i\) individually to the desired output space, which the self-attention layer does not manage to do on its own. It should be noted here, that each output token \(\mathbf{x'}\) is processed by the same feed-forward layer. For more detail, the reader is advised to read the paper.

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()

# get encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# create ids of encoded input vectors
decoder_input_ids = tokenizer("<pad> Ich will ein", return_tensors="pt", add_special_tokens=False).input_ids

# pass decoder input_ids and encoded input vectors to decoder
decoder_output_vectors = model.base_model.decoder(decoder_input_ids).last_hidden_state

# derive embeddings by multiplying decoder outputs with embedding weights
lm_logits = torch.nn.functional.linear(decoder_output_vectors, embeddings.weight, bias=model.final_logits_bias)

# change the decoder input slightly
decoder_input_ids_perturbed = tokenizer("<pad> Ich will das", return_tensors="pt", add_special_tokens=False).input_ids
decoder_output_vectors_perturbed = model.base_model.decoder(decoder_input_ids_perturbed).last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear(decoder_output_vectors_perturbed, embeddings.weight, bias=model.final_logits_bias)

# compare shape and encoding of first vector
print(f"Shape of decoder input vectors {embeddings(decoder_input_ids).shape}. Shape of decoder logits {lm_logits.shape}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `Ich` equal to its perturbed version?: ", torch.allclose(lm_logits[0, 0], lm_logits_perturbed[0, 0], atol=1e-3))

Output:

    Shape of decoder input vectors torch.Size([1, 5, 512]). Shape of decoder logits torch.Size([1, 5, 58101])
    Is encoding for `Ich` equal to its perturbed version?:  True

We compare the output shape of the decoder input word embeddings, i.e. embeddings(decoder_input_ids) (corresponds to \(\mathbf{Y}{0: 4}\), here <pad> corresponds to BOS and "Ich will das" is tokenized to 4 tokens) with the dimensionality of the lm_logits(corresponds to \(\mathbf{L}{1:5}\)). Also, we have passed the word sequence "<pad> Ich will das" and a slightly perturbated version "<pad> Ich will das" together with the encoder_output_vectors through the encoder to check if the second lm_logit, corresponding to "Ich", differs when only the last word is changed in the input sequence ("ein" -> "das").

As expected the output shapes of the decoder input word embeddings and lm_logits, i.e. the dimensionality of \(\mathbf{Y}{0: 4}\) and \(\mathbf{L}{1:5}\) are different in the last dimension. While the sequence length is the same (=5), the dimensionality of a decoder input word embedding corresponds to model.config.hidden_size, whereas the dimensionality of a lm_logit corresponds to the vocabulary size model.config.vocab_size, as explained above. Second, it can be noted that the values of the encoded output vector of \(\mathbf{l}_1 = \text{"Ich"}\) are the same when the last word is changed from "ein" to "das". This however should not come as a surprise if one has understood uni-directional self-attention.

On a final side-note, auto-regressive models, such as GPT2, have the same architecture as transformer-based decoder models if one removes the cross-attention layer because stand-alone auto-regressive models are not conditioned on any encoder outputs. So auto-regressive models are essentially the same as auto-encoding models but replace bi-directional attention with uni-directional attention. These models can also be pre-trained on massive open-domain text data to show impressive performances on natural language generation (NLG) tasks. In Radford et al. (2019), the authors show that a pre-trained GPT2 model can achieve SOTA or close to SOTA results on a variety of NLG tasks without much fine-tuning. All auto-regressive models of 🤗Transformers can be found here.

Alright, that's it! Now, you should have gotten a good understanding of transformer-based encoder-decoder models and how to use them with the 🤗Transformers library.

Thanks a lot to Victor Sanh, Sasha Rush, Sam Shleifer, Oliver Åstrand, ‪Ted Moskovitz and Kristian Kyvik for giving valuable feedback.

Appendix

As mentioned above, the following code snippet shows how one can program a simple generation method for transformer-based encoder-decoder models. Here, we implement a simple greedy decoding method using torch.argmax to sample the target vector.

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# create BOS token
decoder_input_ids = tokenizer("<pad>", add_special_tokens=False, return_tensors="pt").input_ids

assert decoder_input_ids[0, 0].item() == model.config.decoder_start_token_id, "`decoder_input_ids` should correspond to `model.config.decoder_start_token_id`"

# STEP 1

# pass input_ids to encoder and to decoder and pass BOS token to decoder to retrieve first logit
outputs = model(input_ids, decoder_input_ids=decoder_input_ids, return_dict=True)

# get encoded sequence
encoded_sequence = (outputs.encoder_last_hidden_state,)
# get logits
lm_logits = outputs.logits

# sample last token with highest prob
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 2

# reuse encoded_inputs and pass BOS + "Ich" to decoder to second logit
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits

# sample last token with highest prob again
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# concat again
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 3
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# let's see what we have generated so far!
print(f"Generated so far: {tokenizer.decode(decoder_input_ids[0], skip_special_tokens=True)}")

# This can be written in a loop as well.

Outputs:

    Generated so far: Ich Ich

In this code example, we show exactly what was described earlier. We pass an input "I want to buy a car" together with the \(\text{BOS}\) token to the encoder-decoder model and sample from the first logit \(\mathbf{l}_1\) (i.e. the first lm_logits line). Hereby, our sampling strategy is simple to greedily choose the next decoder input vector that has the highest probability. In an auto-regressive fashion, we then pass the sampled decoder input vector together with the previous inputs to the encoder-decoder model and sample again. We repeat this a third time. As a result, the model has generated the words "Ich Ich". The first word is spot-on! The second word is not that great. We can see here, that a good decoding method is key for a successful sequence generation from a given model distribution.

In practice, more complicated decoding methods are used to sample the lm_logits. Most of which are covered in this blog post.