forked from zhaihongjia/hw4
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
2 changed files
with
287 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,215 @@ | ||
| **数字图像与视频处理** | ||
|
|
||
| **第四次作业** | ||
|
|
||
| 姓名:张心怡 班级:自动化66 学号:2160504141 提交日期:2019.3.18 | ||
|
|
||
| | ||
|
|
||
| **摘要** | ||
|
|
||
| 第四次作业主要完成了对图像的滤波处理,选用了MATLAB进行处理。任务一分别用中值滤波和高斯滤波对图像进行了处理并互相对比,MATLAB中用函数fspecial('类型',n);实现。发现中值滤波的降噪力度较强,而高斯滤波较好地保留了图像的细节部分;任务三分别用unsharp masking, Sobel edge detector, and Laplace edge detection,Canny algorithm算子进行边缘检测,并根据处理结果对比了它们的效果。 | ||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
| | ||
|
|
||
| **题目要求:** | ||
|
|
||
| 1.空域低通滤波器:分别用高斯滤波器和中值滤波器去平滑测试图像test1和2,模板大小分别是3x3 , 5x5 ,7x7; 分析各自优缺点; | ||
| 2.-利用固定方差 sigma=1.5产生高斯滤波器. 附件有产生高斯滤波器的方法; 分析各自优缺点; | ||
| 3.利用高通滤波器滤波测试图像test3,4:包括unsharp masking, Sobel edge detector, and Laplace edge detection;Canny algorithm.分析各自优缺点; | ||
|
|
||
| **题目分析:** | ||
|
|
||
| Step1:中值滤波法是一种非线性平滑技术,它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。 | ||
|
|
||
| 进行中值滤波即将邻域中的像素分类排序,用像素邻域内灰度的中值代替该像素的值。 | ||
|
|
||
| MATLAB中进行中值滤波的函数为 fspecial('average',n);n为模板大小。 | ||
|
|
||
| 高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。 | ||
|
|
||
| 高斯滤波的形式为: | ||
| 其中, | ||
|
|
||
|  | ||
|
|
||
| MATLAB中进行中值滤波的函数为 fspecial('gaussian',n);n为模板大小。 | ||
|
|
||
| 中值滤波的优点:对于一定类型的随机噪声,它提供了一种优秀的去噪能力,而且比相同尺寸的线性平滑滤波器的模糊程度明显要低。中值滤波器对处理脉冲噪声非常有效,该种噪声也称为椒盐噪声,因为这种噪声是以黑白点的形式叠加在图像上的。 | ||
|
|
||
| 中值滤波的缺点:模板越大,满足子域相似的条件就越脆弱,于是就越模糊。不能很好地保护图像细节,在图像去噪的同时也破坏了图像的细节部分,从而使图像变得模糊,不能很好地去除噪声点。 | ||
|
|
||
| 高斯滤波的优点:与中值滤波相比,较好地保留了图像的细节部分。 | ||
|
|
||
| 高斯滤波的缺点:在降噪上其实力度比均值差一些。高斯模糊无法完全避免边缘像素信息丢失的缺陷,因为没有考虑像素值的不同。 | ||
|
|
||
|
|
||
|
|
||
| Step2:MATLAB中进行中值滤波的函数为 fspecial('gaussian',n,sigma);n为模板大小,sigma为固定方差。 | ||
|
|
||
|
|
||
|
|
||
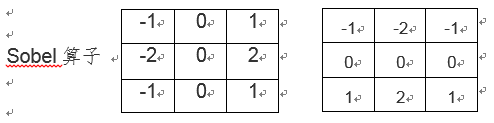
| Step3:Sobel算法是像素图像边缘检测中最重要的算子之一,在机器学习、数字媒体、计算机视觉等信息科技领域起着举足轻重的作用。在技术上,它是一个离散的一阶[差分](https://baike.baidu.com/item/%E5%B7%AE%E5%88%86)算子,用来计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子,将会产生该点对应的梯度矢量或是其法矢量。 | ||
|
|
||
|  | ||
|
|
||
| Laplacian 算子是n维欧几里德空间中的一个二阶微分算子,定义为梯度grad的散度div。可使用运算模板来运算这定理定律。 | ||
|
|
||
| 函数的拉普拉斯算子也是该函数的黑塞矩阵的迹,可以证明,它具有各向同性,即与坐标轴方向无关,坐标轴旋转后梯度结果不变。如果邻域系统是4 邻域,Laplacian 算子的模板为: | ||
|
|
||
| | 0 | 1 | 0 | | ||
| | ---- | ---- | ---- | | ||
| | 1 | -4 | 1 | | ||
| | 0 | 1 | 0 | | ||
|
|
||
| 4邻域Laplacian 算子 | ||
|
|
||
| 如果邻域系统是8 邻域,Laplacian 算子的模板为: | ||
|
|
||
| | 1 | 1 | 1 | | ||
| | ---- | ---- | ---- | | ||
| | 1 | -8 | 1 | | ||
| | 1 | 1 | 1 | | ||
|
|
||
| 8 邻域Laplacian 算子 | ||
|
|
||
| MATLAB中,fspecial函数的功能为产生预定义滤波器,格式: H=fspecial(type)。 | ||
|
|
||
| H=fspecial(' gaussian',n,sigma)高斯低通滤波器 | ||
|
|
||
| H=fspecial('sobel') Sobel水平边缘增强滤波器 | ||
|
|
||
| H=fspecial(' prewitt') Prewitt水平边缘增强滤波器 | ||
|
|
||
| H=fspecial"laplacian' ,alpha)近似二维拉普拉斯运算滤波器 | ||
|
|
||
| H=fspecial('log',n,sigma)高斯拉普拉斯(LoG)运算滤波器 | ||
|
|
||
| H=fspecial(' average',n)均值滤波器 | ||
|
|
||
| H=fspecial('unsharp' ,alpha)模糊对比增强滤波器 | ||
|
|
||
| ① unsharp masking | ||
|
|
||
| 图像的反锐化掩蔽算法可以表示为: | ||
|
|
||
|  | ||
|
|
||
| 其中fs(x,y)表示经过反锐化掩蔽得到的锐化图像,是f(x,y)的模糊形式。 | ||
|
|
||
| ② Sobel edge detector | ||
|
|
||
| 该算子包含两组3x3的矩阵,分别为横向及纵向,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。如果以A代表原始图像,Gx及Gy分别代表经横向及纵向边缘检测的图像灰度值,其公式如下: | ||
|
|
||
|  | ||
|
|
||
| 图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合,来计算梯度的大小。 | ||
|
|
||
|  | ||
|
|
||
| 然后可用以下公式计算梯度方向。 | ||
|
|
||
|  | ||
|
|
||
| 如果角度Θ等于零,即代表图像在该处拥有纵向边缘,左方较右方暗。 | ||
|
|
||
| ③ Laplacian edge detector | ||
|
|
||
|  | ||
|
|
||
| 拉普拉斯算子还可以表示成模板的形式 | ||
|
|
||
| | 0 | 1 | 0 | | ||
| | ---- | ---- | ---- | | ||
| | 1 | -4 | 1 | | ||
| | 0 | 1 | 0 | | ||
|
|
||
| ④ Canny algorithm | ||
|
|
||
| 在图像边缘检测中,抑制噪声和边缘精确定位是无法同时满足的。边缘检测算法通过平滑滤波去除图像噪声的同时,也增加了边缘定位的不确定性;反之,提高边缘检测算子对边缘敏感性的同时,也提高了对噪声的敏感性。Canny算子力图在抗噪声干扰和精确定位边缘之间寻求最佳折中方案。用Canny算子检测图像边缘的步骤如下: | ||
|
|
||
| a)用高斯滤波器平滑图象; | ||
|
|
||
| b)用一阶偏导的有限差分来计算滤波后图像梯度的幅值和方向; | ||
|
|
||
| c)对梯度幅值进行非极大值抑制,其过程为找出图像梯度中的局部极大值点,把其他非局部极大值点置零以得到细化的边缘; | ||
|
|
||
| d)用双阈值算法检测和连接边缘。 | ||
|
|
||
|
|
||
|
|
||
| **处理结果:** | ||
|
|
||
| 1.空域低通滤波器 | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|
|
||
|
|
||
| 3.利用高通滤波器滤波测试图像 | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
|  | ||
|
|
||
| 结果对比: | ||
|
|
||
| ①反锐化掩膜处理结果得到了边缘更加清晰的图像,与预期改进效果一致。但同时看到也会引进一些不希望看到的噪声。 | ||
|
|
||
| ②Sobel 算子是图像处理中的算子之一,主要用作边缘检测。从图像观察,可以看出索贝尔算子并没有将图像边缘完全分离出来。 | ||
|
|
||
| ③拉普拉斯是一种微分算子,其应用强调的是图像中灰度的突变。结合处理后的图像观察,拉普拉斯算子对于test3 corrupt.pgm的边沿检测较为理想,而对于test4 copy.bmp的边缘检测不是很理想。 | ||
|
|
||
| ④Canny算子可以很好的将图像的边缘提取出来。 | ||
|
|
||
|
|
||
|
|
||
| **参考文献:** | ||
|
|
||
| [1] https://blog.csdn.net/zhangfuliang123/article/details/76150175 | ||
|
|
||
| [2] https://blog.csdn.net/baidu_34971492/article/details/78970299 | ||
|
|
||
| [3] http://blog.sina.com.cn/s/blog_c01b063e0102w9c5.html | ||
|
|
||
|
|
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,72 @@ | ||
|
|
||
| 1.�����ͨ�˲������ֱ��ø�˹�˲�������ֵ�˲���ȥƽ������ͼ��test1��2��ģ���С�ֱ���3x3 �� 5x5 ��7x7�� ����������ȱ�㣻 | ||
|
|
||
| img = imread('test2.tif'); | ||
| I = fspecial('gaussian',7,1.5); | ||
| %replicate:ͼ���Сͨ����ֵ��߽��ֵ����չ | ||
| I = imfilter(img,I,'replicate'); | ||
| subplot(1,2,1),imshow(img);title('ԭͼ��'); | ||
| subplot(1,2,2),imshow(I);title('7*7��˹�˲����ͼ��'); | ||
|
|
||
| img = imread('test2.tif'); | ||
| I = fspecial('average',7); | ||
| %replicate:ͼ���Сͨ����ֵ��߽��ֵ����չ | ||
| I = imfilter(img,w,'replicate'); | ||
| subplot(1,2,1),imshow(img);title('ԭͼ��'); | ||
| subplot(1,2,2),imshow(I);title('7*7��ֵ�˲����ͼ��'); | ||
|
|
||
| 3.���ø�ͨ�˲����˲�����ͼ��test3,4������unsharp masking, Sobel edge detector, and Laplace edge detection��Canny algorithm.����������ȱ�㣻 | ||
| I=imread('test4 copy.bmp'); | ||
| Size=size(I); | ||
| I=cast(I,'int32'); | ||
| t=zeros(Size(1)+2,Size(2)+2); | ||
| t=cast(t,'int32'); | ||
| t(2:Size(1)+1,2:Size(2)+1) = I; | ||
| t(:,1)=t(:,2); | ||
| t(:,Size(2)+2)=t(:,Size(2)+1); | ||
| t(1,:)=t(2,:); | ||
| t(Size(1)+2,:)=t(Size(1)+1,:); | ||
| A=1.0; | ||
| for i=2:1:Size(1)+1 | ||
| for j=2:1:Size(2)+1 | ||
| I(i-1,j-1)=t(i,j)*A-(t(i,j)*(-8)+t(i,j-1)+t(i-1,j-1)+t(i-1,j)+t(i,j+1)+t(i+1,j)+t(i+1,j+1)+t(i+1,j-1)+t(i-1,j+1)); | ||
| end | ||
| end | ||
| I=cast(I,'uint8'); | ||
| figure; | ||
| subplot(1,2,1),imshow(I),title('ԭͼ��'); | ||
| subplot(1,2,2),imshow(I),title('usharp masking'); | ||
|
|
||
| I=imread('test4 copy.bmp'); | ||
| subplot(1,2,1),imshow(I),title('ԭͼ��'); | ||
| [N,M]=size(I); | ||
| I=double(I); | ||
| h1=[-1,0,1;-2,0,2;-1,0,1]; | ||
| h2=[-1,-2,-1;0,0,0;1,2,1]; | ||
| Gx=conv2(I,h1,'same'); | ||
| Gy=conv2(I,h2,'same'); | ||
| F=abs(Gx)+abs(Gy); | ||
| for i=1:N | ||
| for j=1:M | ||
| I(i,j)=F(i,j); | ||
| end | ||
| end | ||
| I=uint8(I); | ||
| subplot(1,2,2),imshow(I),title('Sobel'); | ||
|
|
||
| I=imread('test4 copy.bmp'); | ||
| [N,M]=size(I); | ||
| subplot(1,2,1), imshow(I),title('ԭͼ��'); | ||
| t=ones(N,M); | ||
| t=I; | ||
| for i=2:N-1 | ||
| for j=2:M-1 | ||
| I(i,j)=t(i+1,j)+t(i-1,j)+t(i,j+1)+t(i,j-1)-4*t(i,j); | ||
| end | ||
| end | ||
| subplot(1,2,2),imshow(I),title('Laplace'); | ||
|
|
||
| I=imread('test4 copy.bmp'); | ||
| subplot(1,2,1),imshow(I),title('ԭͼ��'); | ||
| I=edge(I,'canny'); | ||
| subplot(1,2,2),imshow(I),title('Canny'); |