LQG: Inverse Optimal Control for Continuous Psychophysics

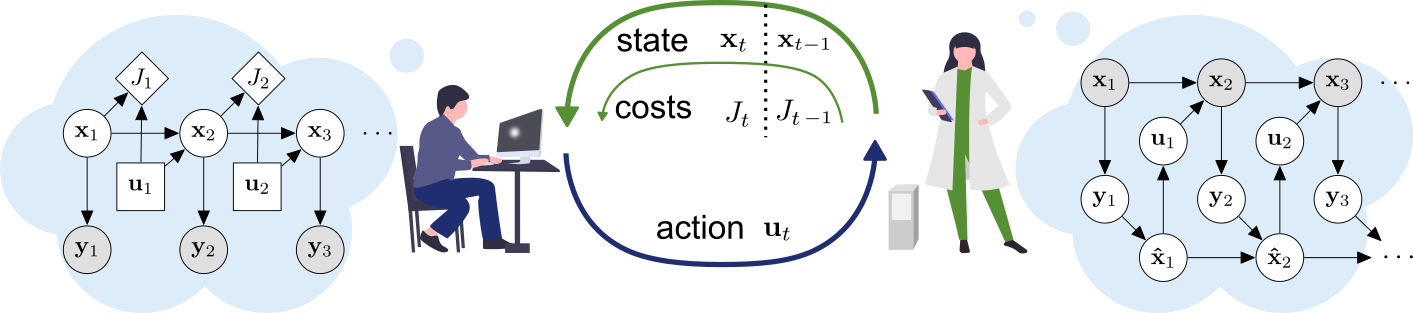
This repository contains the official JAX implementation of the inverse optimal control method presented in the paper:

Straub, D., & Rothkopf, C. A. (2022). Putting perception into action with inverse optimal control for continuous psychophysics. eLife, 11, e76635.

Installation

The package can be installed via pip

python -m pip install lqg

Since publication of our eLife paper, I have substantially updated the package. If you want to use the package as described in the paper, please install an older version <0.20:

python -m pip install lqg==0.1.9

If you want the latest development version, I recommend cloning the repository and installing locally in a virtual environment:

git clone [email protected]:dominikstrb/lqg.git
cd lqg
python -m venv env
source env/bin/activate
python -m pip install -e .

Usage examples

The notebooks in the documentation illustrate how to use the lqg package to define optimal control models, simulate trajectories, and infer parameters from observed data.

• Overview explains the model and its parameters in more detail, including the extension to subjective internal models (based on my tutorial at CCN 2022)
• Data applies the method to data from a tracking experiment

Citation

If you use our method or code in your research, please cite our paper:

@article{straub2022putting,
  title={Putting perception into action with inverse optimal control for continuous psychophysics},
  author={Straub, Dominik and Rothkopf, Constantin A},
  journal={eLife},
  volume={11},
  pages={e76635},
  year={2022},
  publisher={eLife Sciences Publications Limited}
}

Extensions

Signal-dependent noise

This implementation supports the basic LQG framework. For the extension to signal-dependent noise (Todorov, 2005), please see our NeurIPS 2021 paper and its implementation.

Non-linear dynamics

We are currently working on extending this approach to non-linear dynamics and non-quadratic costs. Please check out our NeurIPS 2023 paper and its implementation.