Skip to content

Latest commit

 

History

History
139 lines (87 loc) · 7.17 KB

描述一下感受野.md

File metadata and controls

139 lines (87 loc) · 7.17 KB

计算机视觉中的感受野

感受野作为目标检测和目标跟踪中最常见的一个概念，在面试过程中会被经常提问到。本文将会详细介绍感受野以及其计算方法，希望能够帮助大家更好的理解感受野。

1.感受野的定义

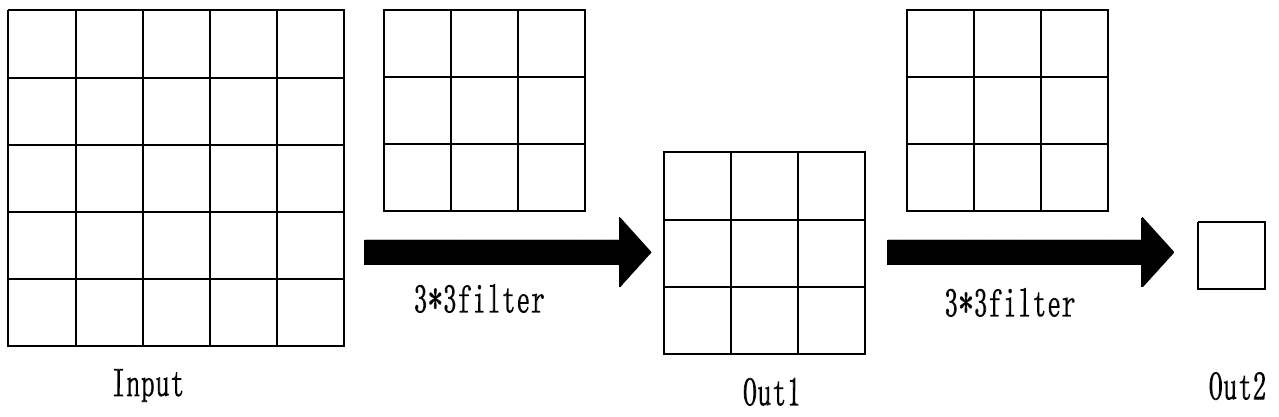
感受野（$Receptive$ $Field$）的定义是卷积神经网络每一层输出的特征图（$feature$ $map$）上的像素点在原始输入图片上映射的区域大小。再通俗点的解释是，特征图上的一个点对应原始输入图片上的区域，如下图所示。

2.感受野的例子

这里举两个例子来简单说明一下感受野。首先是一个5 * 5的输入图经过两层卷积核为3 * 3的卷积操作后得到的感受野是5*5，其中卷积核($filter$)的步长($stride$)为1、$padding$为0，如下图所示：

上图中$Out1$中左上角第一个值是由$Input$中左上角3 * 3区域的值经过卷积计算出来的，即$Out1$中左上角值的感受野是$Input$中左上角3 * 3的区域；

$Out2$中的值是由$Out1$中对应3 * 3的区域经过卷积计算得到的，即$Out2$中的感受野是$Out1$中整个3 * 3的区域；

由此可知$Out2$的值是由$Input$中所有的区域经过两层卷积计算得到的，即$Out2$的感受野是$Input$中所有的5 * 5区域。

再举一个例子，7 * 7的输入图经过三层卷积核为3 * 3的卷积操作后得到$Out3$的感受野为7 * 7，也就是$Out3$中的值是由$Input$所有区域的值经过卷积计算得到，其中卷积核大小、步长和$padding$的值均和上面例子相同，如下图所示：

3.感受野的计算

在计算感受野时有下面几点需要说明：

(1)第一层卷积层的输出特征图像素的感受野的大小等于卷积核的大小。

(2)深层卷积层的感受野大小和它之前所有层的滤波器大小和步长有关系。

(3)计算感受野大小时，忽略了图像边缘的影响，即不考虑padding的大小。

下面给出计算感受野大小的计算公式：

$$ RF_{l+1} = (RF_{l}-1)*\prod_{i=1}^{l}strides_i + f_{l+1} $$

其中$RF_{l+1}$为当前特征图对应的感受野的大小，也就是要计算的目标感受野，$RF_{l}$为上一层特征图对应的感受野大小，f_{l+1}为当前卷积层卷积核的大小，累乘项$strides$表示当前卷积层之前所有卷积层的步长乘积。

以上面举的第二个$sample$为例：

$Out1$层由于是第一层卷积输出，即其感受野等于其卷积核的大小，即第一层卷积层输出的特征图的感受野为3，$RF1$=3；

$Out2$层的感受野$RF2$ = 3 + (3 - 1) * 1 = 5，即第二层卷积层输出的特征图的感受野为5；

$Out3$层的感受野$RF3$ = 3 + (5 - 1) * 1 = 7，即第三层卷积层输出的特征图的感受野为7；

下面给出了由上述方法来计算$Alexnet$和$VGG16$网络中每一层输出特征图的感受野大小的$python$代码：

net_struct = {
    'alexnet': {'net': [[11, 4, 0], [3, 2, 0], [5, 1, 2], [3, 2, 0], [3, 1, 1], [3, 1, 1], [3, 1, 1], [3, 2, 0]],
                'name': ['conv1', 'pool1', 'conv2', 'pool2', 'conv3', 'conv4', 'conv5', 'pool5']},
    'vgg16': {'net': [[3, 1, 1], [3, 1, 1], [2, 2, 0], [3, 1, 1], [3, 1, 1], [2, 2, 0], [3, 1, 1], [3, 1, 1], [3, 1, 1],
                      [2, 2, 0], [3, 1, 1], [3, 1, 1], [3, 1, 1], [2, 2, 0], [3, 1, 1], [3, 1, 1], [3, 1, 1],
                      [2, 2, 0]],
              'name': ['conv1_1', 'conv1_2', 'pool1', 'conv2_1', 'conv2_2', 'pool2', 'conv3_1', 'conv3_2',
                       'conv3_3', 'pool3', 'conv4_1', 'conv4_2', 'conv4_3', 'pool4', 'conv5_1', 'conv5_2', 'conv5_3',
                       'pool5']}}

# 输入图片size
imsize = 224

def outFromIn(isz, net, layernum):
    totstride = 1
    insize = isz
    for layer in range(layernum):
        fsize, stride, pad = net[layer]
        # outsize为每一层的输出size
        outsize = (insize - fsize + 2 * pad) / stride + 1
        insize = outsize
        totstride = totstride * stride
    return outsize, totstride


def inFromOut(net, layernum):
    RF = 1
    for layer in reversed(range(layernum)):
        fsize, stride, pad = net[layer]
        # 感受野计算公式
        RF = ((RF - 1) * stride) + fsize
    return RF


if __name__ == '__main__':
    print("layer output sizes given image = %dx%d" % (imsize, imsize))

    for net in net_struct.keys():
        print('************net structrue name is %s**************' % net)
        for i in range(len(net_struct[net]['net'])):
            p = outFromIn(imsize, net_struct[net]['net'], i + 1)
            rf = inFromOut(net_struct[net]['net'], i + 1)
            print("Layer Name = %s, Output size = %3d, Stride = % 3d, RF size = %3d" % (net_struct[net]['name'][i], p[0], p[1], rf))

其输出结果为：

4.感受野的作用

(1)一般$task$要求感受野越大越好，如图像分类中最后卷积层的感受野要大于输入图像，网络深度越深感受野越大性能越好；

(2)密集预测$task$要求输出像素的感受野足够的大，确保做出决策时没有忽略重要信息，一般也是越深越好；

(3)目标检测$task$中设置$anchor$要严格对应感受野，$anchor$太大或偏离感受野都会严重影响检测性能。

5.有效感受野

$Understanding$ $the$ $Effective$ $Receptive$ $Field$ $in$ $Deep$ $Convolutional$ $Neural$ $Networks$一文中提出了有效感受野($Effective$ $Receptive$ $Field$, $ERF$)理论，论文发现并不是感受野内所有像素对输出向量的贡献相同，在很多情况下感受野区域内像素的影响分布是高斯，有效感受野仅占理论感受野的一部分，且高斯分布从中心到边缘快速衰减，下图第二个是训练后$CNN$的典型有效感受野。

回到这张图，我们看绿色的这个区域，黄色为图像，绿色框扫过时，对于第一列是只扫过一次，也就是参与一次运算，而之后之间的几列均是参与了多次计算。因此，最终实际感受野，是呈现一种高斯分布。

6.总结

感受野属于计算机视觉当中非常重要的基础知识，属于高频面试题，各位小伙伴一定要搞懂呀。

7.引用