Skip to content

Latest commit

 

History

History
120 lines (83 loc) · 6.54 KB

reparameter.md

File metadata and controls

120 lines (83 loc) · 6.54 KB

重参数技巧的简述

大家好，我是灿视。

今天给大家分享一题面试题，是关于重参数技巧的问题。现在说的重参数技巧主要是两方面，一种是用于生成模型中的重参数技巧，一种是目前比较火的 $RepVGG$ 等合并参数的技巧。我这里也主要讨论下这两种技巧，简单的分享一下哈～

水平有限，如有错误，恳请批评指正～

生成模型中的重参数技巧

生成模型很多，主要包括如 $Autoencoder$,$VAE,GAN$ 为代表及其一系列变形的生成模型。我们今天主要聊聊 $VAE$~

当然，不是我的老乡，$VAE$ 许嵩哈。

抱歉，不是我

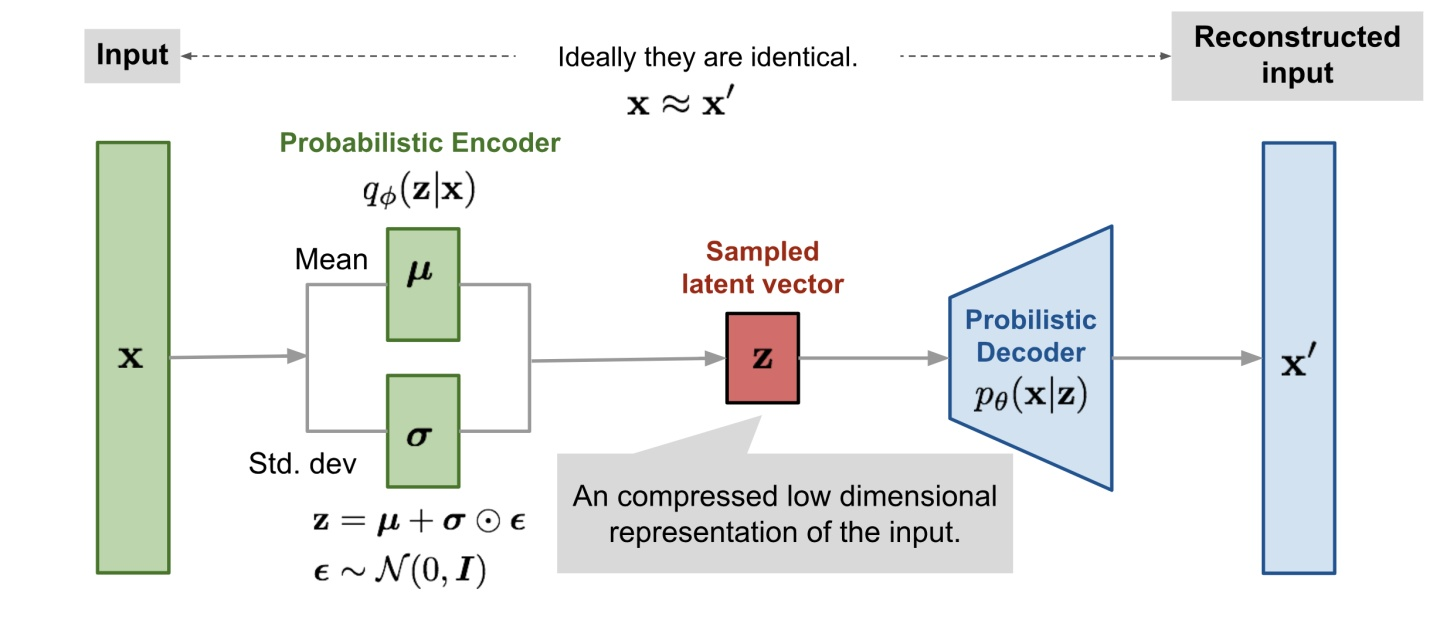
今天说到的 $VAE$ 长这个样子：

具体的 $VAE$ 推导，后面我们会进行详细描述，其中会涉及到变分的东西。今天我们来看下其重参数技巧。

如右边的操作，就是运用了 $reparemerization$ 的技巧。

左边的 $Original$ 方案，即我们从一个分布中，进行采样，来生成一个图片。而由于 $z \sim N(\mu, \sigma)$, 我们应该从 $N(\mu, \sigma)$ 采样, 但这个采样操作对 $\mu$ 和 $\sigma$ 是不可导的, 导致常规的通过误差反传的梯度下降法 (GD) 不能使用。

而通过 $reparemerization$, 我们首先从 $N(0,1)$ 上采样 $\epsilon$, 然后, $z=\sigma \cdot \epsilon+\mu$ 。这样, $z \sim N(\mu, \sigma)$, 而且，$z$ 是编码器网络的输出, 只涉及线性操作, $\quad(\epsilon$ 对神经网络而言只是常数 $)$, 因此, 可 以正常使用梯度下降进行优化。

对于 $VAE$ 具体推导的细节以及其损失函数，我们后面会详细进行介绍的。这里我们只是简单介绍下 $VAE$ 的重参数技巧。

网络结构中的重参数技巧

我这里主要也给大家分享下，在网络结构中的重参数技巧。

  • 卷积层+BN层融合

    卷积层公式为： $$ \operatorname{Conv}(x)=W(x)+b $$ 而BN层公式为： $$ B N(x)=\gamma * \frac{(x-\text { mean })}{\sqrt{\text { var }}}+\beta $$ 然后我们将卷积层结果带入到BN公式中： $$ B N(\operatorname{Conv}(x))=\gamma * \frac{W(x)+b-\text { mean }}{\sqrt{v a r}}+\beta $$ 进一步化简为 $$ B N(\operatorname{Conv}(x))=\frac{\gamma * W(x)}{\sqrt{v a r}}+\left(\frac{\gamma *(b-m e a n)}{\sqrt{v a r}}+\beta\right) $$ 这其实就是一个卷积层, 只不过权盖考虑了BN的参数。

    我们令： $$ \begin{array}{c} W_{\text {fused }}=\frac{\gamma * W}{\sqrt{v a r}} \ B_{\text {fused }}=\frac{\gamma *(b-\text { mean })}{\sqrt{v a r}}+\beta \end{array} $$ 最终的融合结果即为： $$ B N(\operatorname{Conv}(x))=W_{\text {fused }}(x)+B_{\text {fused }} $$

  • RepVGG

RepVGG结构示意图

$RepVGG$ 中主要的改进点包括：

  • 在 $VGG$ 网络的 $Block$ 块中加入了 $Identity$ 和残差分支，相当于把 $ResNet$ 网络中的精华应用 到 $VGG$ 网络中;
  • 模型推理阶段，通过 $Op$ 融合策略将所有的网络层都转换为 $Conv$ $3$ * $3$，便于模型的部署与加速。
  • 网络训练和网络推理阶段使用不同的网络架构，训练阶段更关注精度，推理阶段更关注速度。

Reparameter的操作

上图展示了模型推理阶段的重参数化过程，其实就是一个 OP 融合和 OP 替换的过程。图 A 从结构化的角度展示了整个重参数化流程， 图 B 从模型参数的角度展示了整个重参数化流程。整个重参数化步骤如下所示：

  • 首先通过式3将残差块中的卷积层和BN层进行融合。途中第一个蓝色箭头上方，完成了几组卷积与$BN$的融合。包括执行$Conv$ $3$ * $3$+$BN$层的融合，图中的黑色矩形框中执行$Conv$ $1$ * $1$+$BN$层的融合，图中的黄色矩形框中执行$Conv$ $3$ * $3$(卷积核设置为全1)+$BN$层的融合
    融合的公式为：$\mathrm{W}{i, \mathrm{i}, \mathrm{i}, \mathrm{i}}^{\prime}=\frac{\gamma{i}}{\sigma_{i}} \mathrm{~W}{i, \mathrm{r}, \mathrm{i}, \mathrm{i}}, \quad \mathbf{b}{i}^{\prime}=-\frac{\boldsymbol{\mu}{i} \gamma{i}}{\boldsymbol{\sigma}{i}}+\boldsymbol{\beta}{i}$。

其中$W_{i}$表示转换前的卷积层参数, $\mu_{i}$ 表示BN层的均值, $\sigma_{i}$ 表示BN层的方差, $\gamma_{i}$ 和 $\beta_{i}$ 分别表示BN层的尺店因子和偏移因 子, $W^{i}$和b'分别表示融合之后的卷积的权重和偏置。

  • 将融合后的卷积层转换为$Conv$ $3$ * $3$，即将具体不同卷积核的卷积均转换为具有$3$ * $3$大小的卷积核的卷积。 由于整个残差块中可能包含$Conv$ $1$ * $1$分支和$Identity$两种分支。对于$Conv$ $1$ * $1$分支而言，整个转换过程就是利用$3$ * $3$的卷积核替换$1$ * $1$的卷积核，即将$1$ * $1$卷积核中的数值移动到$3$ * $3$卷积核的中心点即可；对于$Identity$分支 而言，该分支并没有改变输入的特征映射的数值，那么我们可以设置一个$3$ * $3$的卷积核，将所有的$9$个位置处的权重值都设置为1，那么它与输入的特征映射相乘之后，保持了原来的数值。

  • 合并残差分支中的$Conv$ $3$ * $3$。 即将所有分支的权重$W$和偏置$B$叠加起来，从而获得一个融合之后的$Conv$ $3$ * $3$网络层。

    参考代码：

    def _fuse_bn_tensor(self, branch):
      if branch is None:
          return 0, 0
      if isinstance(branch, nn.Sequential):
          kernel = branch.conv.weight
          running_mean = branch.bn.running_mean
          running_var = branch.bn.running_var
          gamma = branch.bn.weight
          beta = branch.bn.bias
          eps = branch.bn.eps
      else:
          ...
      std = (running_var + eps).sqrt()
      t = (gamma / std).reshape(-1, 1, 1, 1)
      return kernel * t, beta - running_mean * gamma / std

总结

今天给大家分享了两个重参数技巧。一个是用于生成模型中，一个是用于网络结构中。对于生成模型，重参数技巧可以解决条件概率不可积分的问题。对于网络结构中，重参数技巧，可以加速网络的前向部署速度。

针对对应的细节，我们会单独说到。欢迎各位持续关注我们哦~