Classifier-guided neural blind deconvolution: a physics-informed denoising module for bearing fault diagnosis under heavy noise (ClassBD)

Overview

This is the official repository of the Machanicial Systems and Signal Processing paper, "Classifier-guided neural blind deconvolution: a physics-informed denoising module for bearing fault diagnosis under heavy noises" Paper

In this work,

1. We introduce a plug-and-play time and frequency neural blind deconvolution module. This module comprises two cascaded components: a quadratic convolutional neural filter and a frequency linear neural filter. From a mathematical perspective, we demonstrate that the quadratic neural filter enhances the filter’s capacity to extract periodic impulses in the time domain. The linear neural filter, on the other hand, offers the ability to filter signals in the frequency domain and it leads to a crucial enhancement for improving BD performance.

2. We develop a unified framework -- ClassBD -- to integrate BD and deep learning classifiers. By employing a deep learning classifier to guide the learning of BD filters, we transition from the conventional unsupervised BD optimization to supervised learning. The fault labels supply useful information in guiding the BD to extract class-distinguishing features amidst background noise. To the best of our knowledge, this is the first BD method of its kind to achieve bearing fault diagnosis under heavy noise while providing good interpretability.

To do list

• Module File
• Full Code
• Detailed Readme

Updates

07/31/2024: We have uploaded four neural network files, BDCNN.py, BDMobileNet.py, BDResNet.py, BDTransformer.py, and related ClassBD files for reference. The input signal should be split to (Batch, 1, 2048).

09/05/2024: We have uploaded full code. Run train_local.py for fast local test, train_wandb.py for online model management.

Note: The dataset should reorgnized as

data/Paderborn/N09_M07_F10/....
data/Paderborn/N15_M01_F10/....
data/Paderborn/N15_M07_F04/....
data/Paderborn/N15_M07_F10/....

and

data/JNU/....

or you can download our reorganized PU datasets in Google Drive PU dataset

Citing

If you find this repo useful for your research, please consider citing it:

@article{LIAO2025111750,
title = {Classifier-guided neural blind deconvolution: A physics-informed denoising module for bearing fault diagnosis under noisy conditions},
journal = {Mechanical Systems and Signal Processing},
volume = {222},
pages = {111750},
year = {2025},
issn = {0888-3270},
doi = {https://doi.org/10.1016/j.ymssp.2024.111750},
author = {Jing-Xiao Liao and Chao He and Jipu Li and Jinwei Sun and Shiping Zhang and Xiaoge Zhang},

Methodology

The proposed framwork

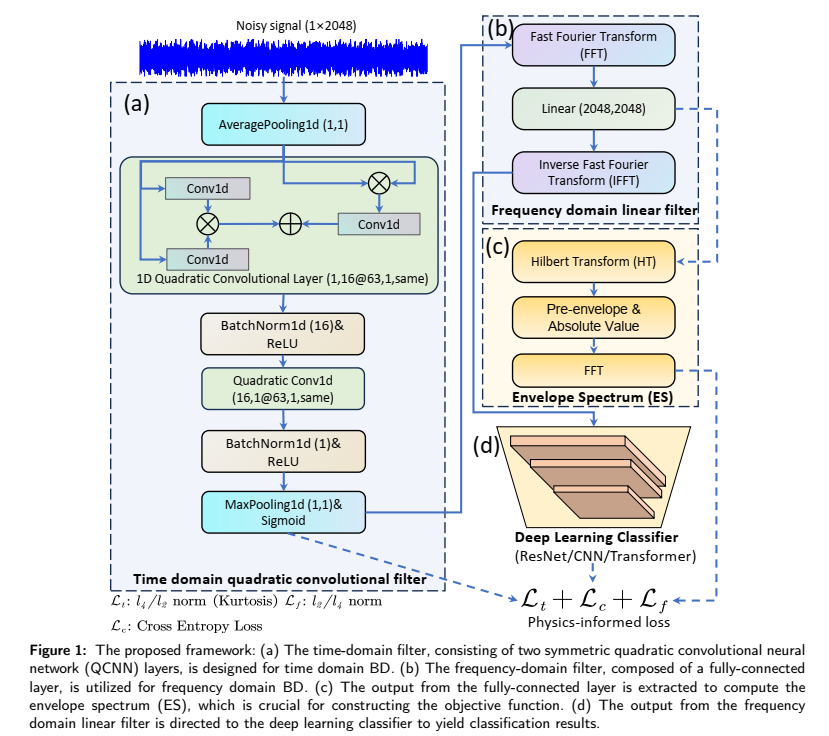
The proposed framework, as illustrated in Figure 1, primarily consists of two BD filters, namely a time domain quadratic convolutional filter and a frequency domain linear filter. These filters serve as a plug-and-play denoising module, and they are designed to perform the same function as conventional BD methods to ensure that the output is in the same dimension as the input.

1. The time domain filter is characterized by two symmetric quadratic convolutional neural network (QCNN) layers. A 16-channel QCNN is employed to filter the input signal (1 $\times$ 2048), and an inverse QCNN layer is used to fuse the 16 channels into one for recovering the input signal.

2. The frequency domain filter, on the other hand, starts with the fast Fourier transform (FFT) with an emphasis on highlighting the discrete frequency components. Subsequently, a linear neural layer filters the frequency domain of the signals, and the inverse FFT (IFFT) is conducted to recover the time domain signal. Moreover, an objective function in the envelope spectrum (ES) is designed for optimization.

After the neural BD filters, 1D deep learning classifiers, such as ResNet, CNN, or Transformer, can be directly used to recognize the fault type. In this paper, we employ a popular and simple network -- wide first kernel deep convolutional neural network (WDCNN)-- as our classifier. Finally, a physics-informed loss function is devised as the optimization objective to guide the learning of the model. This function comprises a cross-entropy loss $\mathcal{L}_c$ and a kurtosis $\mathcal{L}_t$, and $l_2/l_4$ norm $\mathcal{L}_f$. It should be noted that $\mathcal{L}_t$ and $\mathcal{L}_f$ are used to calculate the statistical characteristics of the outputs of the time filter and frequency filter, respectively.