Reference
- RL-Squared (Paper) https://arxiv.org/abs/1611.02779
Practical Matters
Formulation
- A trial is a series of episodes of interaction with a fixed task (MDP), each trial may consist of multiple episodes.
- For each new trial, a separate task is drawn from the distribution and for each episode within the trial a fresh starting state is drawn.
- When an action is produced by the agent, the environment computes a reward, steps forward, computes the next state, and if the episode has terminated it sets the termination flag to 1.
- The next state, reward, and termination flag are concatenated to form the input to the recurrent policy in the next step.
- The recurrent policy conditioned on the hidden state generates the next hidden state and action.
- The objective is to maximize the total discounted reward accumulated during a single trial (consisting of multiple episodes) rather than a single episode.
- As long as different strategies are required for different tasks the agent must act differently according to its belief regarding the current task assigned.
Implementation
- The implementation in this repository uses an Actor-Critic with a memory-augmented policy and value function.
- GRUs are used in order to alleviate vanishing and exploding gradients, and due to their good empirical performance.
- The policy and value function do not rely on a shared GRU, although there is empircal evidence to suggest that this form of weight sharing leads to more stable learning.
- For the policy, the output of the GRU is fed to a fully connected layer followed by a softmax function which forms the distribution over actions for the policy.
- For the value function, the output of the GRU is fed to an MLP consisting of fully connected layers which directly outputs a value estimate.
- The repository contains a minor divergence from the original paper which is that PPO is used as the learning algorithm rather than TRPO as in the original paper.
Experimental Results
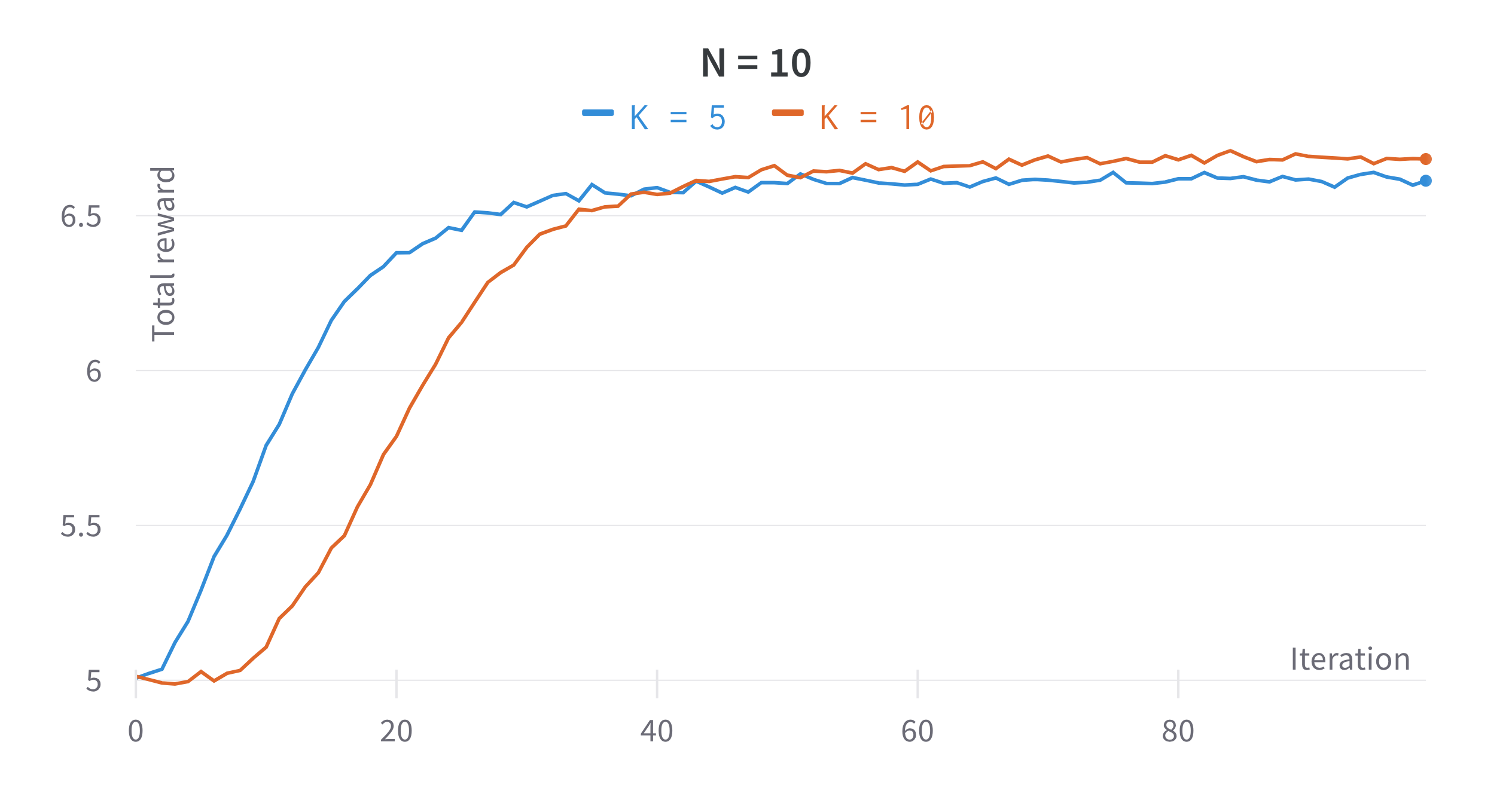
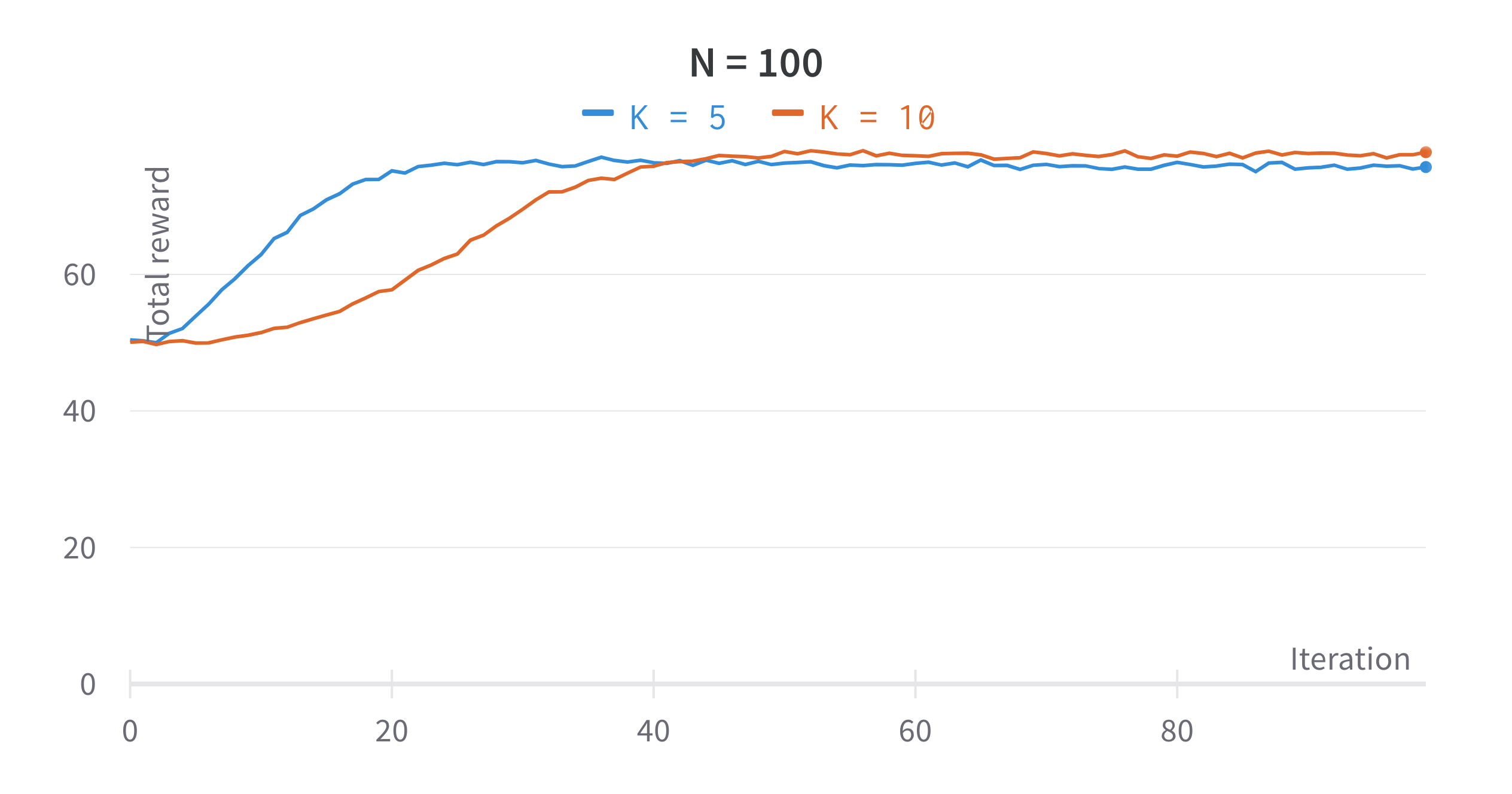
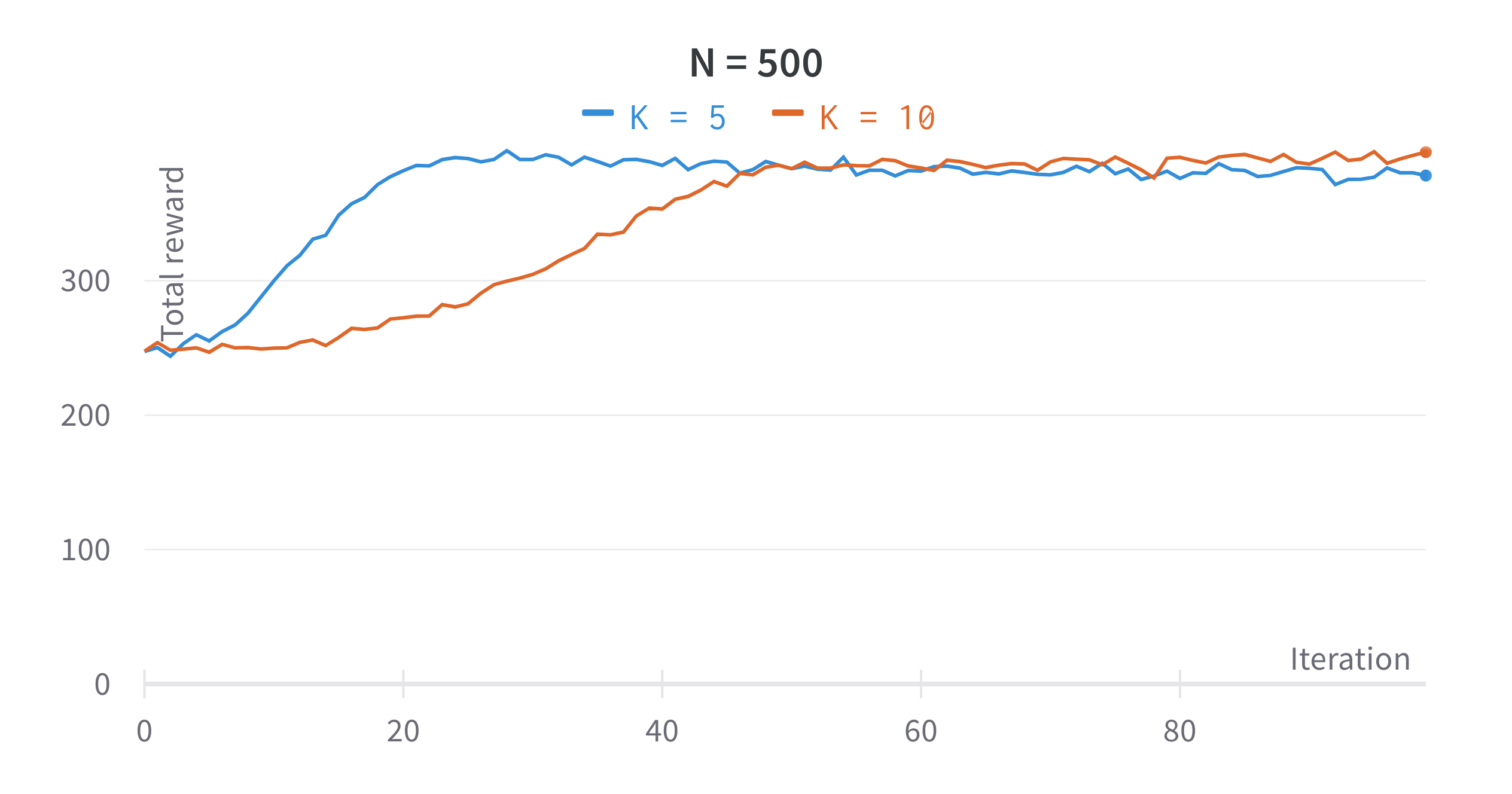
Multi-Armed Bandits
Theory
Abstract
- Deep RL has been successful, but the learning process requires a huge number of trials.
- RL-squared seeks to bridge this gap - rather than designing a fast RL algorithm proposes to represent it in a recurrent neural network and learn it from data.
- RNN receives all information a typical RL algorithm would receive including the state, reward, actions, and termination flags, and retains it state across episodes in a given MDP.
- The activations of the RNN store the state of the "fast" RL algorithm on the current previously unseen MDP.
- After training RL-squared shows performance on new MDPs close to human-designed algorithms with optimality guarantees.
- RL-squared on vision-based navigation task shows the ability to scale.
Bayesian RL
- RL success seems to come at the expense of high sample complexity, this is largely due to the lack of a good prior which results in deep RL agents needing to rebuild knowledge about the world from scratch.
- Bayesian RL provides a framework for incorporating priors into the learning process, but exact computation of the Bayesian update is intractable in all but the simplest cases.
- Practical Bayesian RL methods incorporate a mix of Bayesian and domain-specific ideas to bring down sample complexity.
- But,they tend to make assumptions regarding the environment or become computationally intractable in high-dimensional settings.
RL-Squared
- Rather than hand-designing domain-specific RL algorithms, RL-squared views thee learning process of the agent itself as an objective which can be optimized using standard RL algorithms.
- The objective is averaged across possible MDPs according to a speicifc distribution whcih reflects the prior that we would like to distill into the agent.
- The agent is structured as an RNN which receives past rewards, actions, and termination flags as inputs in addition to the normally received observations.
- Internal state of the RNN is preserved across episodes, it has the capacity to perform learning in its own hidden activations.
- Thus, the learned algorithm also acts as the learning algorithm and can adapt to the task at hand when deployed.
Fast RL via Slow RL
- The paper suggests a different approach for designing better RL algorithms: instead of acting as the designers ourselves, learn the algorithm end-to-end using standard RL techniques.
- The fast RL algorithm is a computation whose state is stored in the RNN activations, and the RNN's weights are learned by a general-purpose slow RL algorithm.