Learn Backpropogation by Implementing it From Scratch

This repository and its README serves as a tutorial of how to implement Backpropagation in Neural Networks in Java. It also includes a tutorial of how to derive backpropagation through an example that will be accompanied by code examples to aid in understanding how to implement backpropagation.

This tutorial presumes a background in machine learning including an understanding of gradient descent, derivation of the delta rule given an arbitrary cost function, and the mechanics of feed-forward prediction in a artificial neural network.

Resources Utilized and Recognition

How to Perform Linear Regression and Logistic Regression using the Code Example

Performing backpropagation by hand

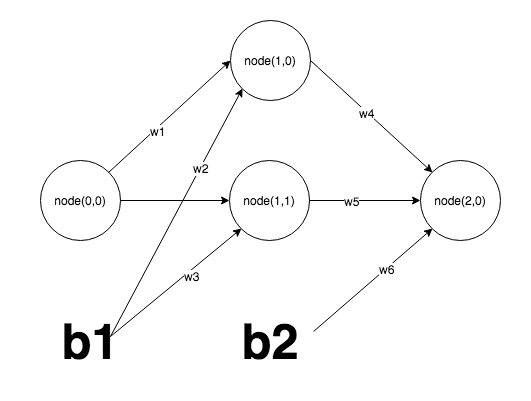
Let's use an extremely simple Neural Network to simplify our computations.

Each Node in the network can be uniquely identified by its layer and its unique index within its respective layer. Assume these values are determined by i and j respectively. Node are identified as Node(i,j).

This representation assumes 1 neuron in the input layer, 2 in the hidden layer, and one in the output layer. Each layer with the exception of the output layer contains a bias. We will use a sigmoid activation function which is represented by the following function.

Let's create a Neuron class that contains the following fields and Constructor. Here the List weights represents the incoming weights for any Neuron in the network (i.e. Node(1,0) will have weights of w1,w2.

public Class Neuron {
      private List<Double> weights;
      private Double out;
      private Double delta;

      public Neuron(Double out) {
          this.out = out;
      }

      public Neuron(int num_weights, boolean bias) {
          Random r = new Random();
          for(int i = 0; i < num_weights; i++) {
              this.weights.add(r.nextDouble());
          }
          if(bias) {
              this.weights.add(1.0);
      }
...

We need a way to calculate the sum of the incoming weights with a previous layer in our network. Let's write a function to do this. Note the result of this will end up feeding into an activation function (sigmoid) to be squashed (between values of 0 and 1).

public static Double activate(Neuron neuron, List<Neuron> inputs) {
  List<Double> weights = neuron.getWeights();

  // ensure calculation will be valid
  if(weights.size() != inputs.size() + 1) {
  	throw new RuntimeException();
  }
  
  Double activation = weights.get(weights.size()-1); // accomdate the bias
  for (int i = 0; i <= weights.size(); i++) {
  	activation += weights.get(i) * inputs.get(i).getOut();
  }
  return activation;
}

We'll include the static method activation_function that represents the output of a sigmoid activation function.

public static Double sigmoid(Double activation) {
	return 1.0 / (1.0 + Math.exp(-1.0 * activation));
}

Let's also create a class to represents our Neural Network. We'll represent a layer as a List of Neuron Objects, and our Neuron Network as a List<> of layers.

In our constructor we initialize our inputs randomly based upon the paramater num_inputs. Then we proceed to add our hidden and output layers given the next wo paramaters: num_hidden and num_outputs.

public class Neural {

    private List<List<Neuron>> network;
    private List<Neuron> inputs;

    /**
     * Constructor
     *
     * @param num_inputs
     * @param num_hidden
     * @param num_outputs
     */
    public Neural(int num_inputs, int num_hidden, int num_outputs) {

        Random r = new Random();
        for (int i = 0; i < num_inputs; i++) {
            inputs.add(new Neuron(r.nextDouble()));
        }

        List<Neuron> layer = new ArrayList<>();

        // Generate the Hidden Layers
        for (int i = 0; i < num_hidden; i++) {
            layer.add(new Neuron(num_inputs, true));
        }

        // Construct the network thus far
        this.network.add(layer);

        // Construct the output Layer
        layer = new ArrayList<>();

        // Generate the Output Layer
        for (int i = 0; i < num_outputs; i++) {
            layer.add(new Neuron(num_hidden, true));
        }
        this.network.add(layer);

    }
...

In order for us to perform the feed-forward portion of training our neural network so that we can determine output of our neural network for a given piece of training data, we'll end up doing the following calculations

out_Node(0,0) // has been initialized to some random value

net_Node(1,0) = w1 * out_Node(0,0) + w3 * b1
net_Node(1,1) = w2 * out_Node(0,0) + w3 * b1

out_Node(1,0) = sigmoid(net_Node(1,0))
out_Node(1,1) = sigmoid(net_Node(1,1))

net_Node(2,0) = w4 * Node(1,0) + w5 * Node(1,1) + w6 * b2

result = sigmoid(net_Node(2,0)) // this the output of our feedforward algorithm

Let's represent this functionality in a method in our Neural Network class.

public List<Neuron> forward_propagation() {
    List<Neuron> input = this.inputs; // we begin with the input layer
    for (List<Neuron> layer : this.network) {
        List<Neuron> tmp = new ArrayList<>(); // Create the next layer
        for (Neuron neuron : layer) {
            Double activation = Neuron.activate(neuron, input);
            neuron.setOut(Neuron.sigmoid(activation));
            tmp.add(neuron); // the hidden layer becomes the input
        }
        input = tmp;
    }
    return input; // return the output layer after iterations done
}

Now let's get to the good stuff, the backpropogation algorithm. In traditional gradient descent for linear regression we predict the output given a peice of training data in the following method

output = w1 * x1 + w2 * x2 + b

However, we have an cost function in the form of

cost(x):
    return 1/2 * (expected - output)  ^ 2

We can use gradient descent to find out the partial derivatives with respect to each weight, and update our weights so that we converge to minimum after some arbitrary number of iterations.

learning_rate // random value

// Use Chain rule
dCost/dw1 = dError/doutput * d_output/d_w1
d_Cost/dOutput = (expected - output)
doutput/dw1 = -1 * (x1)
dCost/dw1 = -1 * (expected - output) * x1

// update w1 given the learning rate
w1 = w1 - learning_rate * dCost/dw1

Let's use a similar approach to find out the partial derivatives for our weights w4, w5, and w6 in our neural network. We assume the same cost function as used previously. Let's use w4 as an example.

dCost/d(w4) = dCost/d(out_Node(2,0)) * d(out_Node(2,0))/d(netNode(2,0)) * d(netNode(2,0))/d(w4)

/**
Let's break this calculation into parts
**/

// First Partila derivative in chain rule
dCost/d(out_node(2,0)) = (expected - output_Node(2,0))
x = dCost/d(out_node(2,0))

// Second Partial Derivative
d(sigmoid(net_node(2,0)) = sigmoid(net_node(2,0)) * (1 - sigmoid(net_node(2,0)))
d(out_Node(2,0))/d(netNode(2,0)) = d(sigmoid(net_node(2,0))
y = d(out_Node(2,0))/d(netNode(2,0))

// Third Partial Derivative
d(netNode(2,0))/d(w4)) = out_NetNode(1,0)
z = d(netNode(2,0))/d(w4))

// calculate the partial derivative
dCost/d(w4) = x * y * z

We can extrapolate this method to calculate w4, w5, and w6. What about w1, w2, and w3?

dCost/d(w1) = d(Cost)/d(out_Node(1,0)) * d(out_Node(1,0))/d(net_Node(1,0)) * d(netNode(1,0))/d(w1)

// First Partial
d(Cost)/d(out_Node(1,0)) = d(Cost)/d(out_Node(2,0)) * d(out_Node(2,0))/d(out_Node(1,0)) 

d(out_Node(2,0))/d(out_Node(1,0)) = d(out_Node(2,0))/d(net_Node(2,0)) * d(net_Node(2,0))/d(out_Node(1,0))
d(out_Node(2,0))/d(net_Node(2,0)) = sigmoid(net_node(2,0)) * (1 - sigmoid(net_node(2,0)))
d(net_Node(2,0))/d(out_Node(1,0)) = w4

d(Cost/d(out_Node(2,0)) = (expected - output_Node(2,0))

d(Cost)/d(out_Node(1,0)) = (expected - output_Node(2,0)) * w4

// Second
d(out_Node(1,0))/d(net_Node(1,0)) = sigmoid(net_node(1,0)) * (1 - sigmoid(net_node(1,0)))

// Third
d(netNode(1,0)/d(w1) = out_Node(0,0)

// Result
dCost/d(w1) = (expected - output_Node(2,0)) * w4 * (sigmoid(net_node(1,0)) * (1 - sigmoid(net_node(1,0)))) * out_Node(0,0)

We can see that this follows a very recursive pattern. Notice how we must calculate d(Cost)/d(out_Node(1,0)) * d(out_Node(1,0))/d(net_Node(1,0)) for the partial Derivative for the weight 1. We must do the same calculation for weight 4 in the form: dCost/d(out_Node(2,0)) * d(out_Node(2,0))/d(netNode(2,0)). This repitition provides us a method for calculation.

Let's define the delta for a given node(i,j) as d(Cost)/d(net_Node(i,j)). This allows us to simplify our calculations and precalculate portions of our calculations as we move from right to left through the network. In our backward pass we will calculate the delta per node.

public void backward_propagate_error(List<Double> expected) {
    List<Neuron> prev_layer = null;
    for(int count = this.network.size()-1; count >= 0; count--) {
        List<Neuron> layer = this.network.get(count);
        List<Double> errors =  new ArrayList<>();
        if(count != this.network.size()-1) {
            for(int j = 0; j < layer.size(); j++) {
                double error = 0.0;
                for (Neuron neuron : prev_layer) {
                    List<Double> weights = neuron.getWeights();
                    error += weights.get(j) * neuron.getDelta();
                }
                errors.add(error);
            }
        } else {
            for(int j = 0; j < layer.size(); j++) {
                errors.add(expected.get(j) - layer.get(j).getOut());
            }
        }
        for(int j = 0; j < layer.size(); j++) {
            Neuron neuron = layer.get(j);
            neuron.setDelta(errors.get(j) * Neuron.transfer_derivative(neuron.getOut()));
        }
        count += 1;
        prev_layer = layer;
    }
}

Note the backpropogation rule is different for the output layer versus all subsequent hidden layers. From this point we can use the delta rule to update our weights.