Theory

Creating Your World

Let's take a simple city with six nodes representing six intersections without lights and no turn restrictions. This means that at every interesection you may turn in any direction and won't spend any extra time. So only time spent on edges (road segments between intersections) will be taken into account.

Now you make a→b→c→f and need 10 + 11 + 12 = 33 seconds (green):

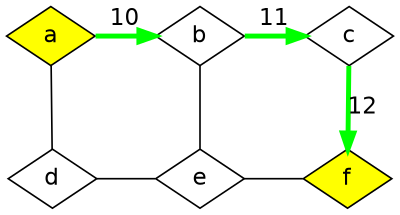
The next day you make a→d→e→f need 9 + 8 + 7 = 24 seconds (blue):

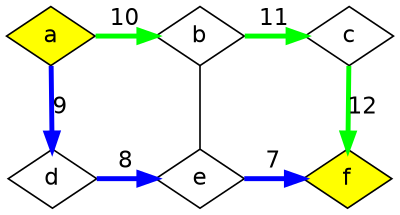
The blue a→d→e→f would be currently the “optimal” route.

But on the third day you make a short round-trip a→b→e→d→a in 15 + 5 + 9 + 9 = 38 seconds (red). This trip even does not reach f and on the first segment a→b it is slower than the green one (because of more traffic).

Now we get three possible paths from a to f:

1. a→d→e→f is the blue one with 24 seconds
2. a→b→c→f is a combination of green and red. Minimum is 33 seconds (10 + 11 + 12, maximum is 38 seconds (15 + 11 + 12)
3. a→b→e→f with a combination of green, red, and blue and 22 to 27 seconds

Which is the fastest route?

Depends. You can already forget about a→b→c→f, which is ALWAYS slower than the other two. But what probability of success do you expect?

All edges have one value, except for a→b, which has two: 10 and 15. If you're optimistic about your next trip and hope to repeat your best time, then the path a→b→e→f will take 10 + 5 + 7 = 22, which is better than a→d→e→f 9 + 8 + 7 = 24.

If you want to “make sure” you arrive in time, expect you'll need 15 seconds for a→b and therefore a→d→e→f is the better choice.

Now imagine your world with dozens or hundreds of nodes and as many values per edge!