"Em engenharia elétrica, a transformada alpha-beta(α-β-γ), também conhecida como transformada de Clarke, é uma transformação matemática aplicada para simplificar a análise de circuitos trifásicos. Conceitualmente ela é similar a transformada dq0. Uma aplicação muito útil da transformada alpha-beta é a geração de um sinal de referência usado para controle da modulação do vetor espacial."
traduzido da Wikipedia
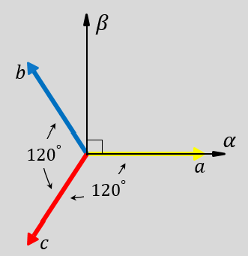
(Fonte: Mathworks)
A Transformada de Clarke consiste em um sistema cujo eixo alpha está completamente alinhado com a fase A e o eixo beta está em quadratura com este. Isso fornece duas curvas senoidais defasadas de 90 graus. Quando o sistema trifásico está em equilíbrio essas duas curvas em alpha-beta tem módulo igual. Quando o sistema desequilibra os módulos se tornam diferentes.
(Fonte: Mathworks)
"A ransformação direto-quadratura-zero (dq0) é um tensor que rotaciona o eixo de referência de um sistema vetorial de três elementos ou uma matriz de três por três elementos com o intuito de simplificar a análise. A transformada dq0 é o produto da transformada de Clarke e de Park, primeiramente proposto po Robert H. Park em 1929."
traduzido da Wikipedia

(fonte: MathWorks)
A transformada de Park, quando aplicada a um sistema trifásico equilibrado, apresenta valores de d, q e zero constantes. Quando um desequilíbrio surge esses valores começam a oscilar (com o dobro da frequência do sistema original). No momento de calcular a transformada de Park podemos alinhar com a fase A do nosso sistema trifásico o eixo d ou o eixo q. Neste projeto o eixo escolhido para alinhar com a fase A foi o eixo d, que resulta em um gráfico similar ao mostrado abaixo.
(fonte: MathWorks)
A interface gráfica deste programa foi pensada para simplificar ao máximo sua utilização. Sendo assim, esta explicação será breve. Os passos para uma execução usual do programa são:
-
Executar o arquivo main.py. Como o nome sugere, ele é o arquivo principal do programa e executa todas as instruções. Com o arquivo sendo corretamente executado, uma janela irá se abrir;
-
Na janela aberta é possível inserir todos os dados do programa. Vale ressaltar que o programa não gerará os gráficos até que todos os campos estejam devidamente preenchidos;
-
As unidades estão explicitadas ao lado dos campos, com exceção dos campos "unit" e "Faults", que são menus de lista com opções predeterminadas.
-
Os campos de texto, como "frequency [Hz]:", somente aceitam números, o caracter decimal de ponto "." e o caracter de sinal negativo "-" para evitar eventuais erros que possam atrapalhar a execução do código;
-
Não há uma ordem específica na qual os dados devam ser preenchidos.
-
Quando o preenchimento tiver sido realizado por completo basta clicar no botão "Calculate" para gerar os gráficos nas condições configuradas.
-
Em seuida uma nova janela se abrirá para mostrar os gráficos. Esta janela é interativa, permitindo manipular o tamanho dos gráficos, aproximar ou afastar, analisar intervalos específicos, etc.
-
Para salvar os gráficos basta clicar no símbolo de disquete na janela dos gráficos e escolher o formato do arquivo e onde armazená-lo. Atente-se que o programa não salva automaticamente estes dados!
-
Caso deseje gerar novos gráficos basta repetir as etapas de 2 a 6. Note que os gráficos previamente gerados serão sobrescritos, então caso queira manter os dados obtidos é importante executar o passo 8!