Merge pull request #21 from ITSLeeds/add-p2

add p2/index.qmd

DESCRIPTION

@@ -20,6 +20,9 @@ Imports:
     spDataLarge,
     DT,
     calendar,
-    reticulate
+    reticulate,
+    stplanr,
+    tmap,
+    spData
 Remotes:
     nowosad/spDataLarge

p2/index.qmd

@@ -0,0 +1,292 @@
+---
+title: "Origin-destination data"
+# subtitle: '<br/>Practical'
+# author: "Malcolm Morgan and Robin Lovelace"
+# date: 'University of Leeds `r # Sys.Date()()`<br/><img class="img-footer" alt="" src="https://comms.leeds.ac.uk/wp-content/themes/toolkit-wordpress-theme/img/logo.png">'
+toc: true
+execute: 
+  cache: true
+bibliography: ../tds.bib
+---
+
+# Review Homework
+
+You should now be familiar with the basics of R and the `tidyverse`. If you have not completed these tasks go back and do them first:
+
+- Read Chapters 2, 3, and 4 of [Reproducible road safety research with R](https://itsleeds.github.io/rrsrr/basics.html)
+- Read Chapters 3 and 5 of [R for Data Science](https://r4ds.had.co.nz/data-visualisation.html)
+
+# Getting started with GIS in R
+
+Note that this practical takes sections from Chapters 2 - 8 of [Geocomputation with R](https://r.geocompx.org). You should expand your knowledge by reading these chapters in full.
+
+
+## Pre-requisites {-}
+
+You need to have a number of packages installed and loaded.
+Install the packages by typing in the following commands into RStudio (you do not need to add the comments after the `#` symbol)
+
+If you need to install any of these packages use:
+
+```{r echo = T, results = 'hide', eval = FALSE}
+install.packages("sf")  # Install a package from CRAN
+remotes::install_github("Nowosad/spDataLarge")   # install from GitHub using the remotes package
+```
+
+```{r echo = T, results = 'hide', warning=FALSE, message=FALSE}
+library(sf)          # vector data package 
+library(tidyverse)   # tidyverse packages
+```
+
+- It relies on **spData**, which loads datasets used in the code examples of this chapter:
+
+```{r 03-attribute-operations-2, echo = T, results = 'hide',warning=FALSE, message=FALSE}
+library(spData)  # spatial data package 
+```
+
+1. Check your packages are up-to-date with `update.packages()`
+1. Create an RStudio project with an appropriate name for this session (e.g. `practical2`)
+1. Create appropriate folders for code, data and anything else (e.g. images)
+1. Create a script called `learning-OD.R`, e.g. with the following command:
+
+```{r, eval = F, echo = T, results = 'hide'}
+dir.create("code") # 
+file.edit("code/learning-OD.R")
+```
+## Basic sf operations
+
+We will start with a simple map of the world. Load the `world` object from the `spData` package.  Notice the use of `::` to say that you want the `world` object from the `spData` package.
+
+```{r, echo = T, results = 'hide'}
+world = spData::world
+```
+
+Use some basic R functions to explore the `world` object. e.g. `class(world)`, `dim(world)`, `head(world)`, `summary(world)`. Also view the `world` object by clicking on it in the Environment panel.
+
+`sf` objects can be plotted with `plot()`.
+
+```{r, warning=FALSE}
+plot(world)
+```
+
+Note that this makes a map of each column in the data frame. Try some other plotting options
+
+```{r}
+plot(world[3:6])
+plot(world["pop"])
+```
+
+## Basic spatial operations
+
+Load the `nz` and `nz_height` datasets from the `spData` package.
+
+```{r, echo = T, results = 'hide'}
+nz = spData::nz
+nz_height = spData::nz_height
+```
+
+We can use `tidyverse` functions like `filter` and `select` on `sf` objects in the same way you did in Practical 1.
+
+```{r, echo = T, results = 'hide'}
+canterbury = nz %>% filter(Name == "Canterbury")
+canterbury_height = nz_height[canterbury, ]
+```
+
+In this case we filtered the `nz` object to only include places called `Canterbury` and then did and intersection to find objects in the `nz_height` object that are in Canterbury.
+
+This syntax is not very clear. But is the equivalent to
+
+```{r, echo = T, eval=FALSE}
+canterbury_height = nz_height[canterbury, , op = st_intersects]
+```
+
+There are many different types of relationships you can use with `op`. Try `?st_intersects()` to see more. For example this would give all the places not in Canterbury
+
+```{r, eval=FALSE}
+nz_height[canterbury, , op = st_disjoint]
+```
+
+![Topological relations between vector geometries, inspired by Figures 1 and 2 in Egenhofer and Herring (1990). The relations for which the function(x, y) is true are printed for each geometry pair, with x represented in pink and y represented in blue. The nature of the spatial relationship for each pair is described by the Dimensionally Extended 9-Intersection Model string. ](https://r.geocompx.org/figures/relations-1.png)
+
+
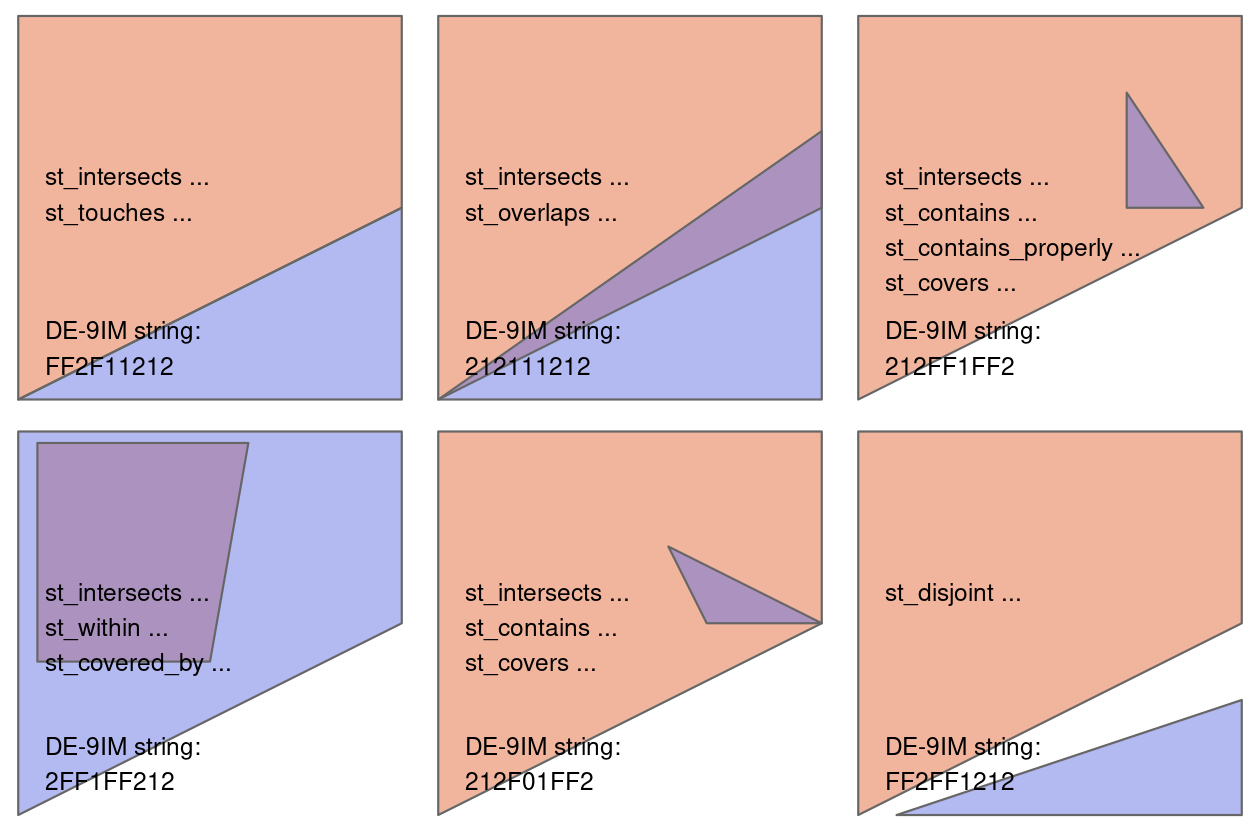+# Getting started with OD data
+
+In this section we will look at basic transport data in the R package **stplanr**.
+
+Load the  `stplanr` package as follows:
+
+```{r, echo = T, results = 'hide'}
+library(stplanr)
+```
+
+The `stplanr` package contains some data that we can use to demonstrate principles in Data Science, illustrated in the Figure below. Source: Chapter 1 of R for Data Science [@grolemund_r_2016] [available online](https://r4ds.had.co.nz/introduction.html).
+
+![](https://d33wubrfki0l68.cloudfront.net/571b056757d68e6df81a3e3853f54d3c76ad6efc/32d37/diagrams/data-science.png)
+
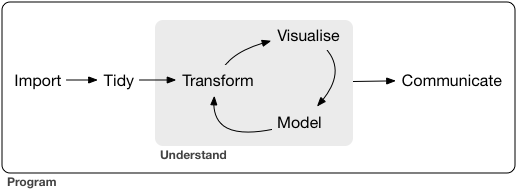+First we will load some sample data:
+
+```{r, echo=FALSE}
+od_data = stplanr::od_data_sample
+```
+
+You can click on the data in the environment panel to view it or use `head(od_data)`
+Now we will rename one of the columns from `foot` to `walk`
+
+```{r, echo=FALSE}
+od_data = od_data %>%
+  rename(walk = foot)
+```
+
+Next we will made a new dataset `od_data_walk` by taking `od_data` and piping it (`%>%`) to `filter` the data frame to only include rows where `walk > 0`. Then `select` a few of the columns and calculate two new columns `proportion_walk` and `proportion_drive`.
+
+```{r, echo=FALSE}
+od_data_walk = od_data %>% 
+  filter(walk > 0) %>% 
+  select(geo_code1, geo_code2, all, car_driver, walk) %>% 
+  mutate(proportion_walk = walk / all, proportion_drive = car_driver / all)
+```
+
+We can use the generic `plot` function to view the relationships between variables
+
+```{r}
+plot(od_data_walk)
+```
+
+R has built in modelling functions such as `lm` lets make a simple model to predict the proportion of people who walk based on the proportion of people who drive.
+
+```{r, echo=FALSE}
+model1 = lm(proportion_walk ~ proportion_drive, data = od_data_walk)
+od_data_walk$proportion_walk_predicted = model1$fitted.values
+```
+
+We can use the `ggplot2` package to graph our model predictions.
+
+```{r}
+ggplot(od_data_walk) +
+  geom_point(aes(proportion_drive, proportion_walk)) +
+  geom_line(aes(proportion_drive, proportion_walk_predicted))
+```
+
+Exercises
+
+1. What is the class of the data in `od_data`?
+2. Subset (filter) the data to only include OD pairs in which at least one person (`> 0`) person walks (bonus: on what % of the OD pairs does at least 1 person walk?)
+3. Calculate the percentage who cycle in each OD pair in which at least 1 person cycles
+4. Is there a positive relationship between walking and cycling in the data?
+5. Bonus: use the function `od2line()` in to convert the OD dataset into geographic desire lines
+
+```{r, echo=FALSE, eval=FALSE}
+#1
+class(od_data)
+```
+
+```{r, echo=FALSE, eval=FALSE}
+#2 
+od_data_walk = od_data %>% 
+  filter(walk > 0)
+nrow(od_data_walk) / nrow(od_data) * 100
+```
+
+```{r, echo=FALSE, eval=FALSE}
+#3
+od_data = od_data %>% 
+  filter(bicycle > 0) %>% 
+  mutate(perc_cycle = (bicycle/all) * 100)
+```
+
+```{r, echo=FALSE, eval=FALSE}
+#4
+od_data_new = od_data %>% 
+  filter(walk > 0, bicycle>0 ) %>% 
+  select(bicycle, walk, all) 
+
+model = lm(walk ~ bicycle, weights = all, data = od_data_new)
+od_data_new$walk_predicted = model$fitted.values
+
+ggplot(od_data_new) +
+  geom_point(aes(bicycle, walk, size = all)) +
+  geom_line(aes(bicycle, walk_predicted))
+```
+
+
+```{r, echo=FALSE, eval=FALSE}
+#5
+desire_lines = od2line(flow = od_data, zones)
+plot(desire_lines)
+```
+
+# Processing origin-destination data in Bristol
+
+This section is based on [Chapter 12 of Geocomputation with R](https://geocompr.robinlovelace.net/transport.html). You should read this chapter in full in your own time.
+
+We need the `stplanr` package which provides many useful functions for transport analysis and `tmap` package which enables advanced mapping features.
+
+```{r, echo = T, results = 'hide', warning=FALSE, message=FALSE}
+library(stplanr)
+library(tmap)
+```
+
+
+We will start by loading two datasets:
+
+```{r}
+od = spDataLarge::bristol_od
+zones = spDataLarge::bristol_zones
+```
+
+Explore these datasets using the functions you have already learnt (e.g. `head`,`nrow`).
+
+You will notice that the `od` datasets has shared id values with the `zones` dataset. We can use these to make desire lines between each zone. But first we must filter out trips that start and end in the same zone.
+
+```{r, echo = T, results = 'hide', warning=FALSE, message=FALSE}
+od_inter = filter(od, o != d)
+desire_lines = od2line(od_inter, zones)
+```
+Let's calculate the percentage of trips that are made by active travel
+
+```{r, echo = T, results = 'hide'}
+desire_lines$Active = (desire_lines$bicycle + desire_lines$foot) /
+  desire_lines$all * 100
+```
+
+Now use `tmap` to make a plot showing the number of trips and the percentage of people using active travel.
+
+```{r, echo = T, results = 'hide', warning=FALSE, message=FALSE}
+desire_lines = desire_lines[order(desire_lines$Active),]
+
+tm_shape(desire_lines) +   # Define the data frame used to make the map
+  tm_lines(col = "Active", # We want to map lines, the colour (col) is based on the "Active" column
+           palette = "plasma", # Select a colour palette
+           alpha = 0.7,    # Make lines slightly transparent
+           lwd = "all") +  # The line width (lwd) is based on the "all" column
+  tm_layout(legend.outside = TRUE) + # Move the ledgend outside the map
+  tm_scale_bar()           # Add a scale bar to the map
+```
+
+Now that we have geometry attached to our data we can calculate other variables of interest. For example let's calculate the distacne travelled and see if it relates to the percentage of people who use active travel.
+
+```{r}
+desire_lines$distance_direct_m = as.numeric(st_length(desire_lines))
+```
+
+Note the use of `as.numeric` by default `st_length` and many other functions return a special type of result with `unit`. Here we force the results back into the basic R numerical value. But be careful! The units you get back depend on the coordinate reference system, so check your data before you assume what values mean.
+
+```{r, warning=FALSE, message=FALSE}
+ggplot(desire_lines) +
+  geom_point(aes(x = distance_direct_m, y = Active, size = all)) +
+  geom_smooth(aes(x = distance_direct_m, y = Active))
+```
+
+The blue line is a smoothed average of the data. It shows a common concept in transport research, the distance decay curve. In this case it shows that the longer the journey the less likely people are to use active travel. But this concept applies to all kinds of travel decisions. For example you are more likely to travel to a nearby coffee shop than a far away coffee shop. Different types of trip have different curves, but most people always have a bias for shorter trips.
+
+
+# Homework
+
+1. Read Chapters 2-5 of [Geocomputation with R](https://r.geocompx.org/transport.html) 
+2. Work though Sections 13.1 to 13.4 of the Transport Chapter in [Geocomputation with R](https://r.geocompx.org/transport.html)
+3. Bonus: Read more about using the [tmap package](https://r-tmap.github.io/tmap/)
+4. Bonus: Read more about the [ggplot2 package](https://ggplot2.tidyverse.org/)
+5. Bonus: Read Chapter 7 & 8 of [Geocomputation with R](https://r.geocompx.org/transport.html) 
+
+
+# References