数据结构系统学习和实现
- 数组基础
- 栈
- 队列
- 链表
- 树结构
- 集合
- 典型应用
- 集合的时间复杂度分析
- 映射-map
- 堆和优先队列
- 线段树-segment-tree
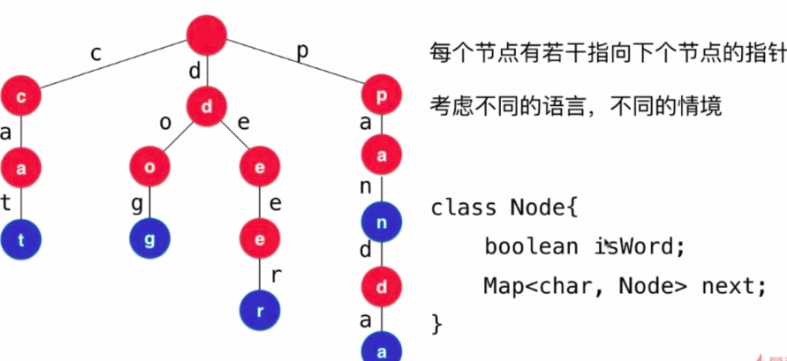
- Trie-字典树-前缀树
- 并查集-union-find
- 平衡二叉树和AVL树
- 红黑树(统计性能更优)
- 哈希表
- 总结
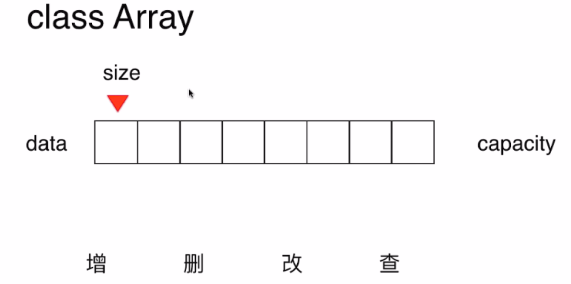
数组的最大的有点:快速查询. 数组最好应用于"索引有语意"的情况 但并非所有语意的索引都适用于数组:例如索引长度过长
- 制作自己的数组
- 索引没有语意,如何标识没有元素?
- 如何添加元素?
- 如何删除元素?
- 基于Java的数组,二次等装属于我们自己的数组类
- 使用泛型
- 数据结构可以放置"任何"数据类型
- 不可以是基本的数据类型,只能是类对象.基本数据类型: boolean,byte,char,short,int,long,float,double
- 每个基本数据类型都有对应的包装类:Boolean,Byte,Character,Short,Integer,Long,Float,Double
- 自动扩容
- 在添加元素时判断是空间已填满
- 若填满则按照原由的data.length()的两倍进行扩容
- 扩容原理:
- 生成新的data数组
- 将原由的data数组赋值到新的的扩容数组中(遍历赋值存在效率问题)
- data引用新的数组
- 原由的数组将不再被引用,JVM进行垃圾回收
- O(1),O(n),O(lgn),O(nlogn),O(n^2):大O描述的是算法的运行时间和输入数据之间的关系
- 添加操作O(n),resize O(n),通常以最坏的情况为基准:
- addLast(e) O(1)
- addFirst(e) O(n)
- add(index,e) O(n/2)=O(n) 可以理解成平均需要挪n/2个元素
- 删除操作O(n),resize O(n):
- removeLast(e) O(1)
- removeFirst(e) O(n)
- removeIndex(index,e) O(n/2)=O(n)
- 修改操作O(1):
- set(index,e) O(1)
- 查询操作O(n):
- get(index) O(1)
- contains(e) O(n)
- find(e) O(n)
- 栈也是一种线性结构
- 相比数组,栈对应的操作是数组的子集
- 只能从一端添加元素,也只能从另一端取元素
- 取元素这一端称为栈顶
- 无处不再的Undo操作(编辑器撤销)
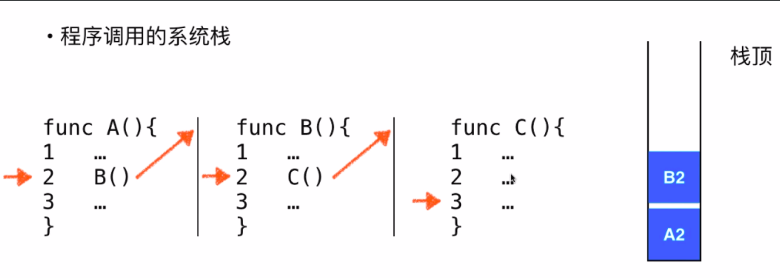
- 程序调用的系统栈:用于记录程序中断的地方,当子函数执行完后中断记录进行出栈,回到之前中断的地方继续执行
- 括号匹配 - 编译器检查代码时的应用
- 思路:栈顶元素反映了在嵌套的层次关系中,最近的需要匹配的元素
实现ArrayStack<E>
- void push(E)
- E pop
- E peek()
- int getSize()
- boolean isEmpty()
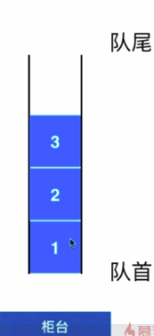
- 队列也是一种线性结构
- 相比数组,队列对应的操作是数组的子集
- 只能从另一端(队尾)添加元素,只能从另一点(队首)取出元素
实现Queue<E>
- void enqueue(E)
- E dequeue()
- E getFront()
- int getSize()
- boolean isEmpty()
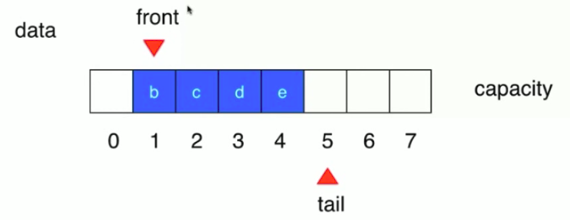
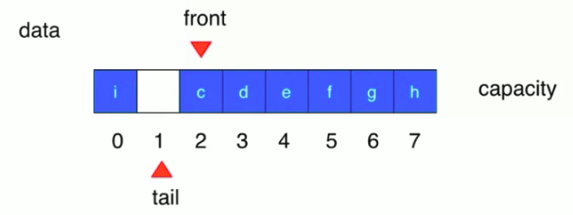
- 删除队首元素时间复杂度为O(n)
- front == tail 队列为空
- (tail + 1)%capacity == front 队列为满
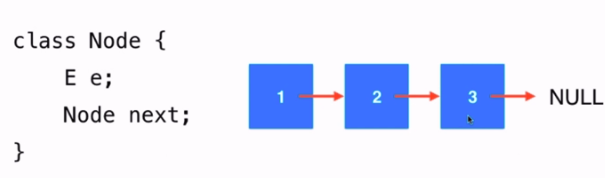
- 简单的动态的数据结构
- 更加深入的理解引用(或者指针)
- 更深入的理解递归
优点:真正的动态,不需要处理固定容量的问题
缺点:丧失了随机访问的能力(即不能更具给定的索引来立即取出元素)
1.在链表头添加元素
- node.next = head
- head = node
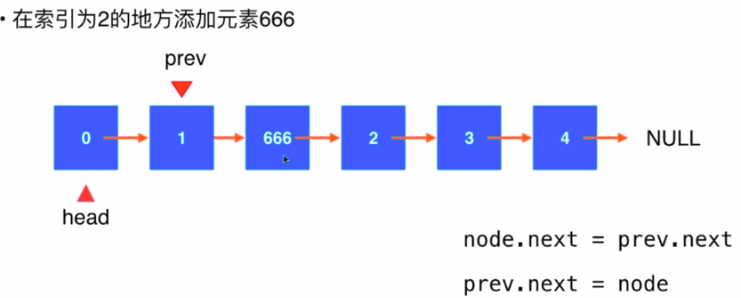
2.在链表中间添加元素:
- 需要一个prev指针,进行遍历
- 生成一个新的node
- node.next = prev.next
- prev.next = node
- 关键:
- 找到要添加的节点的前一个节点
- 两步操作不能调换
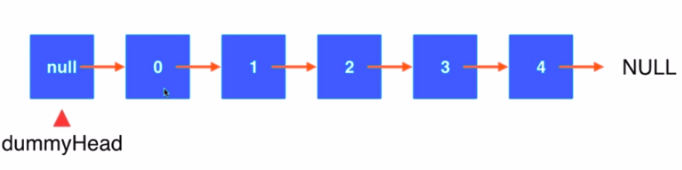
3.虚拟头节点
- 有意的设置一个为null的dummyHead
- 即浪费一个空间为后续编写逻辑的方便
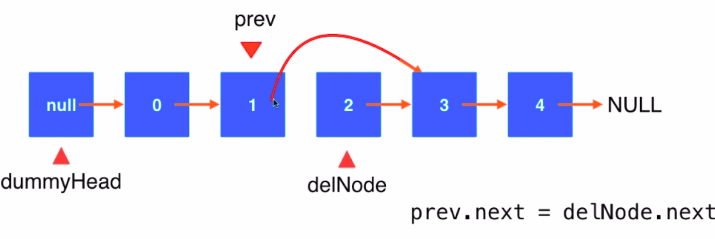
4.删除某一链表元素
- 找到要删除的前一个元素的位置prev
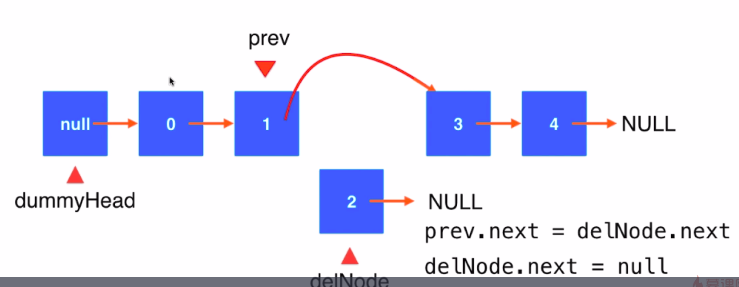
- prev.next = delNode.next
- 释放将删除的指针与链表断开联系使得JVM能够进行垃圾回收: delNode.next = null
- 增删改查的复杂度都是O(n)
- 如果只是对链表头进行操作:O(1)
两种栈的耗时点:
- 数组栈主要在缩容和扩容的地方需要对元素进行遍历赋值
- 链表需要对每个添加的元素进行new操作来添加新的空间
- 相对优异的比较需要综合考量,差异不是很大
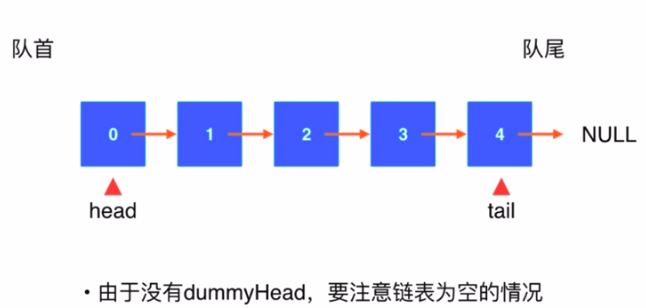
- 队列需要在队尾添加元素,在队首删除元素
- 链表需要两个指针一个head,一个tail
- head端为队首,tail端为队尾
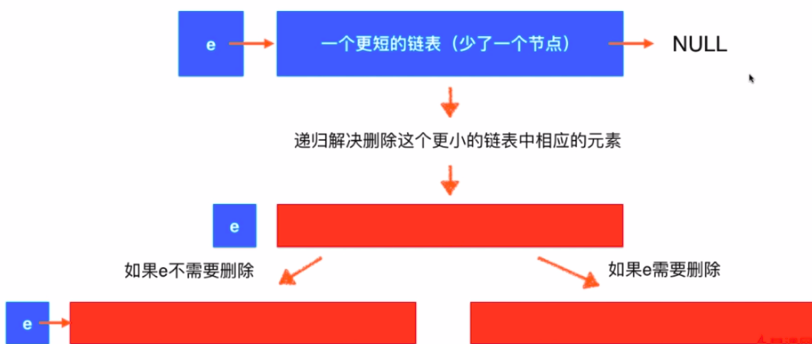
LeetCode203题链表移除指定元素:Solution2
- 本质上,将原来的问题,转换为更小的问题
- 列举:数组求和
- Sum(arr[0...n-1]) = arr[0] + Sum(arr[1...n-1])
- Sum(arr[1...n-1]) = arr[1] + Sum(arr[2...n-1])
- ...
- 注意递归函数的"宏观"语意
- 递归函数就是一个函数,完成一个功能
- 解决链表中删除元素的问题
主要数结构:
- 二分搜索树(Binary Search Tree)
- 平衡二叉树: AVL;红黑树
- 堆;并查集
- 线段树;Trie(字典树,前缀树):主要用于处理字符串数据
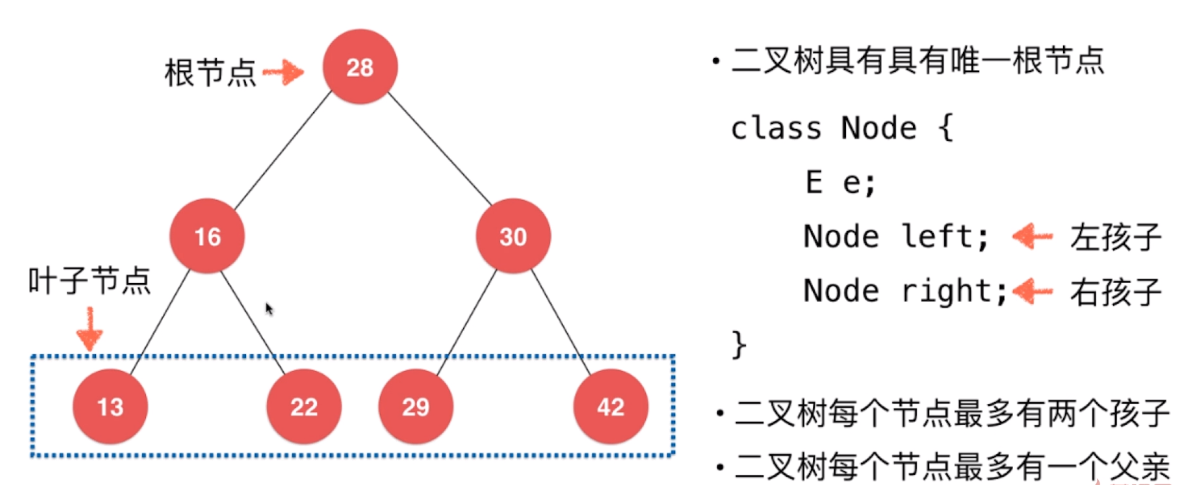
- 二叉树具备天然递归结构
- 每个节点的左孩子树也是二叉树
- 每个节点的右孩子树也是二叉树
- 二叉树不一定是"满"的
- 二分搜索树是二叉树
- 二分搜索树的每一个节点的值:
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
- 每一棵子树也是二分搜索树
- 存储的元素具有可比较性
- 遍历操作就是把所有节点都访问一遍
- 访问的原因和业务有关
- 例如: 当发现某个题答案出错了,需要对每个学生的成绩都加上几分,这时就需要对每个元素进行遍历
- 在线性结构下,遍历是极其容易的
- 在树结构下,也没有那么难
遍历方式:
- 深度优先遍历:
- 前序遍历: 根->左->右
- 中序遍历: 左->根->右
- 后序遍历: 左->右->根
- 后序遍历的应用: 手动释放内存,先处理孩子节点
- 广度优先遍历:
- 层序遍历
- 广度优先的意义:
- 更快的找到对应的元素
- 更多应用于搜索策略上
- 常用于算法设计-最短路径
- 删除节点的情况:
- 删除的节点左子树为null
- 删除的节点右子树为null
- 删除节点的左右子树都不为null(两种思路:1.删除当前节点后找前驱节点,2.删除当前节点后找后继节点)
集合的特点:去重
回忆二分搜索树,是不能存放重复的元素的,所以二分搜索树是实现集合非常好的底层数据结构
Set<E>
- void add(E) //不能添加重复元素
- void remove(E)
- void boolean contains(E)
- int getSize()
- boolean isEmpty()
- 客户统计
- 词汇量的统计
- 增 add LinkedListSet:O(n) , BSTSet:O(h)=O(logn)
- 查 contains LinkedListSet:O(n) , BSTSet:O(h)=O(logn)
- 删 remove LinkedListSet:O(n) , BSTSet:O(h)=O(logn)
- 存储(键,值) 数据对的数据结构(key,value)
- 非常容易使用链表或者二分搜索树来实现
- Map<K,V>
- void add(K,V)
- V remove(K)
- boolean contains(K)
- V get(K)
- void set(K,V)
- int getSize()
- boolean isEmpty()
- 链表实现Map映射
- 二分搜索树实现Map映射
- 词频统计
- 有序映射:键具有顺序
- 无序映射:键没有顺序
- 多重映射:键可以重复
常见的底层实现:基于映射的底层实现直接包装出集合来
util包中的HashSet的底层实现就是通过HashMap来实现的
-
普通队列: 先进先出;后进后出
-
优先队列: 出队顺序和入队顺序无关;和优先级相关
-
为什么使用优先队列?
- 动态选择优先级最高的任务执行
- 游戏中的AI攻击最近目标
-
Interface Queue <---implement---- PriorityQueue<E>
- void enqueue(E)
- E dequeue() //出队为优先级最高的元素
- E getFront()
- int getSize()
- boolean isEmpty()
-
时间复杂度分析:
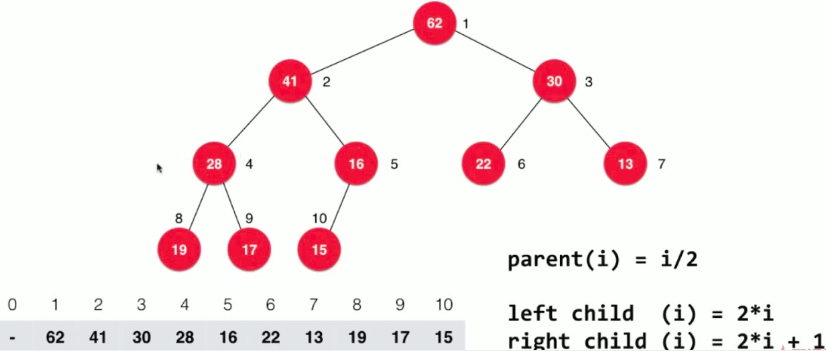
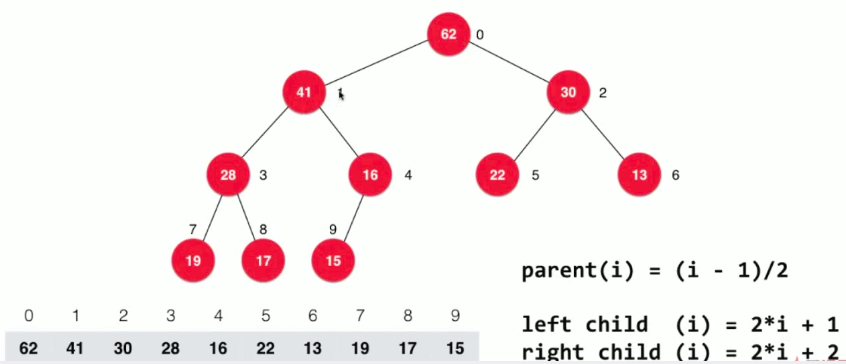
- 二叉堆是一棵完全二叉树
- 完全二叉树: 把元素顺序排列成树的形状
- 区别于满二叉树:满二叉树是有多少层就确定了有多少个节点
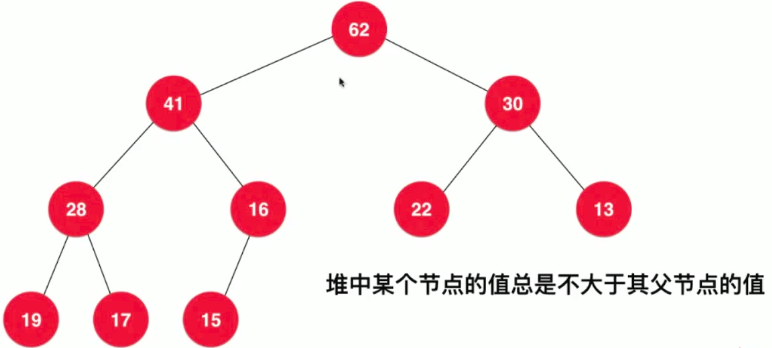
- 最大堆: 根节点值大于等于其所有子节点的值
- 最小堆: 与最大堆相反,根节点小于等于其所有子节点的值
- 注意: 层次低的节点的值不一定大于层次高的节点的值,所以节点大小与层次无关
- 存放方式1:
- 存放方式2:
- 将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn)
- heapify的过程,算法复杂度为O(n)
- 在1000000个元素中嗯如何选出前100名?
- 在N个元素中选出前M个元素
- 使用排序的时间复杂度--> NlogN
- 使用有限队列时间复杂度--> NlogM
- 使用优先队列,维护当前看到的前M个元素
- 需要使用最小堆
- LeetCode-347题,使用自定义的优先队列来求前k个频次最高的元素
- LeetCode-347题,使用java中的优先队列来求前k个频次最高的元素
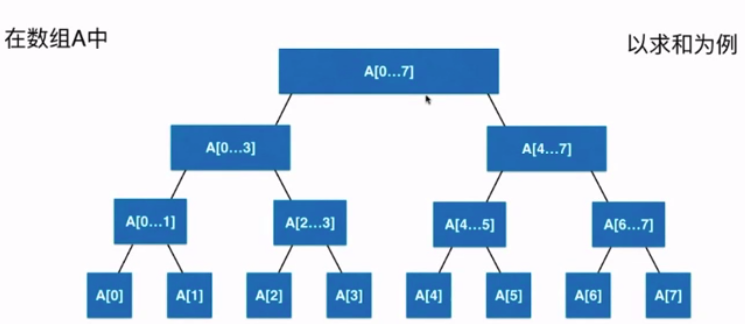
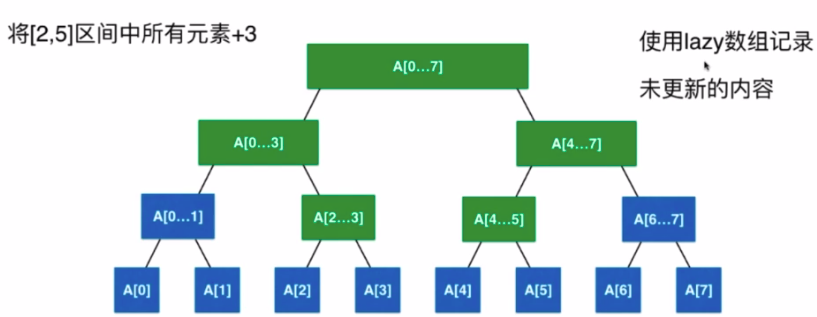
- 经典的区间染色问题?
- 另一类经典问题:区间查询
- 例如:2017年注册用户中消费最高的用户?
- 消费最多的用户?
- 学习时间最长的用户?
- 线段树不是完全二叉树
- 线段树是平衡二叉树
- 定义: 对于整棵树来说,最大深度与最小的深度之间相差最多只能为1
- 堆也是平衡二叉树(完全二叉树,一定满足平衡二叉树)
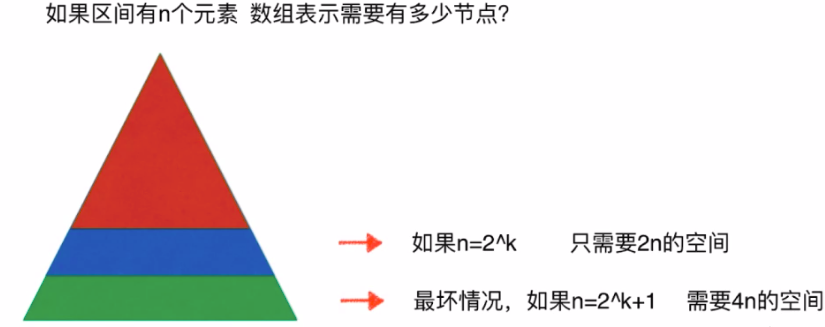
- 如果区间有n个元素,数组表示需要多少个节点? 需要4n的空间
- 我们的线段树不考虑添加元素,即区间固定,使用4n的静态空间即可
- 对于一组数据,主要支持两个动作:
- union(p,q) , 将这两个数据和这两个数据的集合连接起来
- isConnected(p,q) , 查询这两个数据是否属于同一个集合 ----> find(p) == find(q)
- Quick Find 数组结构实现并查集
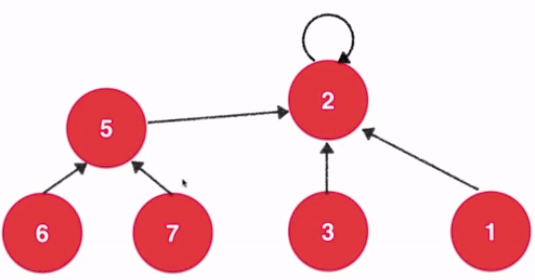
- Quick Union 树结构实现并查集
- 并查集基于size的优化,即元素少的向元素多的合并
- 并查集基于rank的优化,即深度低的向深度高的合并
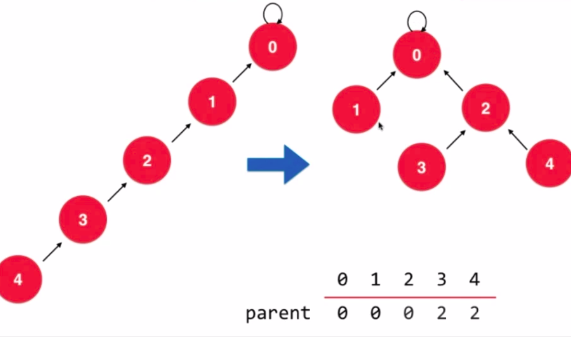
- 并查集基于路径压缩的优化,即降低树的高度
- 并查集路径压缩,使用递归压缩至一层
并查集实现:
路径压缩:
- 网络中节点间的连接状态
- 网络是一个抽象的概念: 用户之间形成的网络
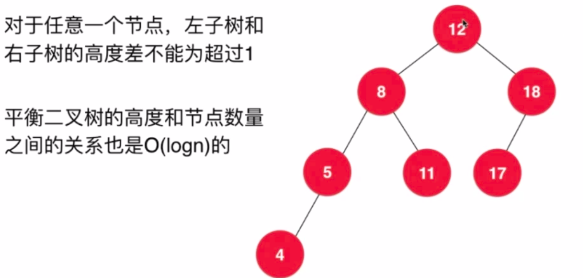
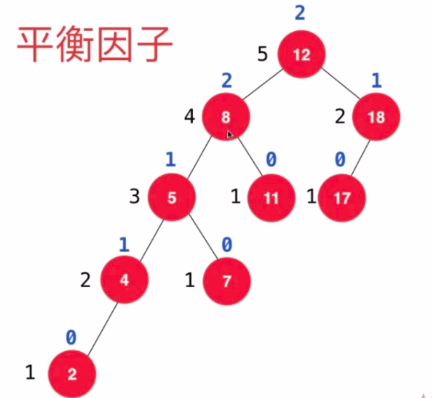
- 定义: 对于任意一个节点,左子树和右子树的高度差不能超过1
- 是一种能够实现自平衡的树
- 维护平衡思路:
- 平衡被破坏只可能发生在插入元素的过程中,导致父节点的高度改变
- 所以应该在加入节点后,沿着节点向上维护平衡性
- 判断条件: 左右子树的平衡因子做差再取绝对值 <= 1 ,则表示是平衡二叉树,否则不是
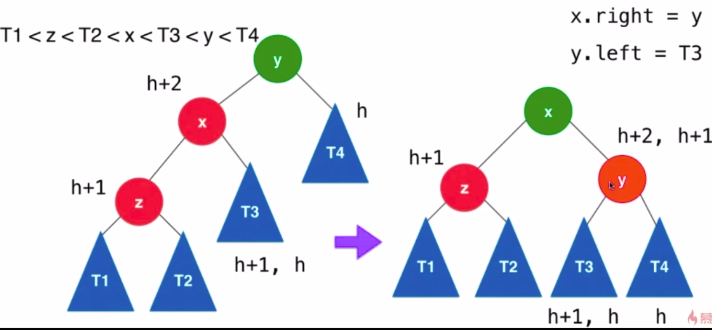
- LL : 插入节点为不平衡节点的左孩子的左孩子
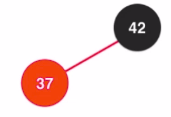
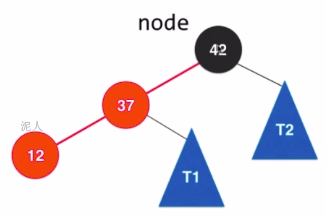
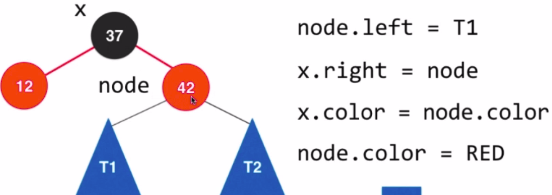
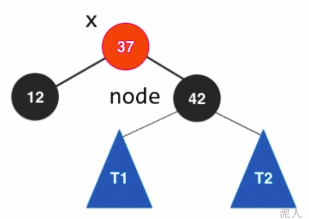
- 解决方法 : 右旋转 rightRotate(node)
- RR : 插入节点为不平衡节点的右孩子的右孩子
- 解决方法 : 左旋转 leftRotate(node)
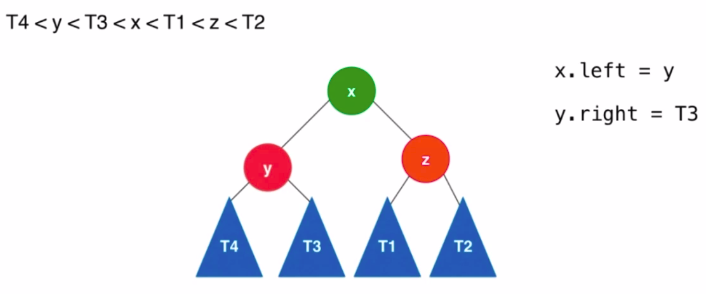
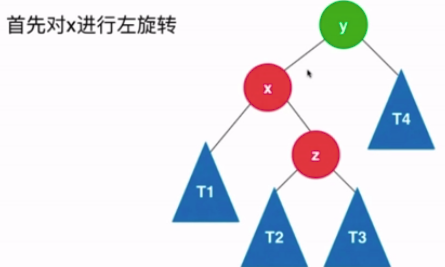
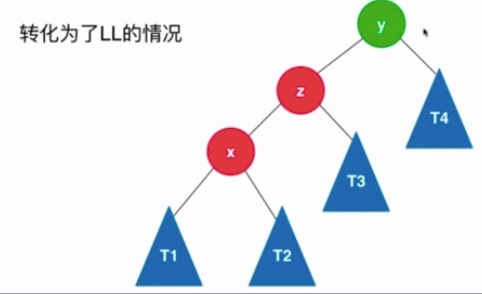
- LR : 新插入的节点为不平衡节点的左孩子的右孩子
- 解决方法 : 先对x进行左旋转得到LL的情况,然后再参照LL的处理方式对y进行右旋转
- RL : 新插入的节点为不平衡的节点的右孩子的左孩子
- 解决方法 : 先对x进行右旋转得到RR的情况,然后再参照RR的处理方式对y进行左旋转
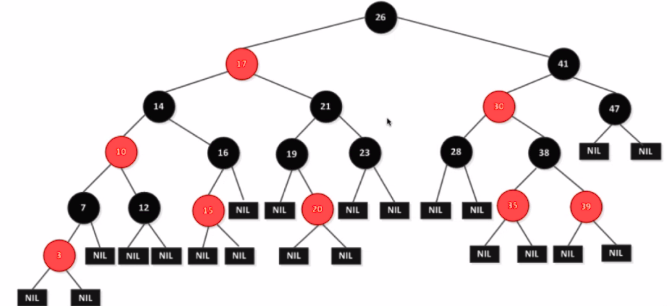
- 每个节点或者是红色的,或者是黑色的
- 根节点是黑色的
- 每个叶子节点(最后的空节点)是黑色的
- 如果一个节点是红色的,那么他的孩子节点都是黑色的
- 从任意一个节点到叶子节点,经过的黑色节点是一样的
- 满足二分搜索树的基本性质
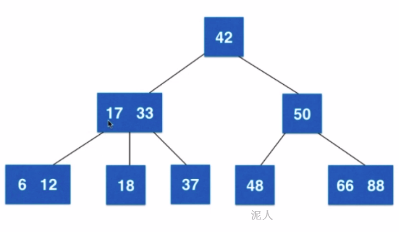
- 节点可以存放一个元素或两个元素
- 每一个节点或者有2个孩子或者有3个孩子---2-3树由来
- 2-3树是一种绝对平衡的树,即左右子树的高度是一定相等的
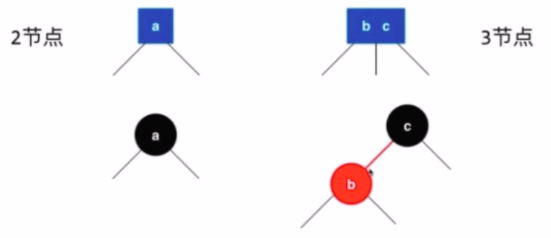
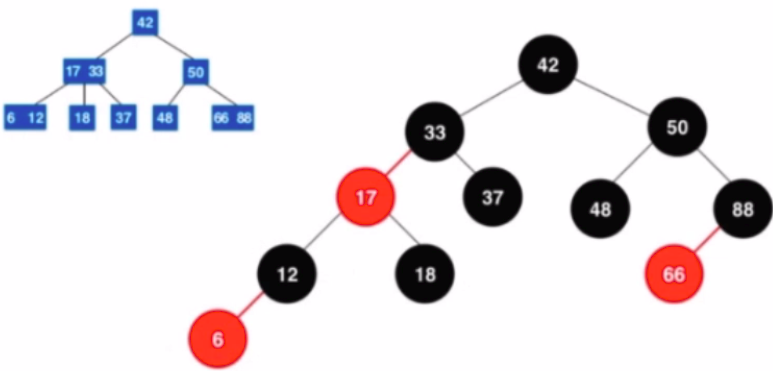
- 对节点进行标为红色表示该节点和父亲节点是一个并列的关系,一起存放在3节点中
- 所有红色节点都是左倾斜的
- 红黑树是保持"黑平衡"的二叉树,严格意义上,不是平衡二叉树
- 添加新元素可能发生的情况:
- 2-3树中添加一个新元素
- 或者添加进2-节点,形成一个3-节点
- 或者添加进3-节点,暂时形成一个4-节点
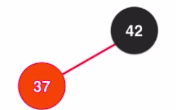
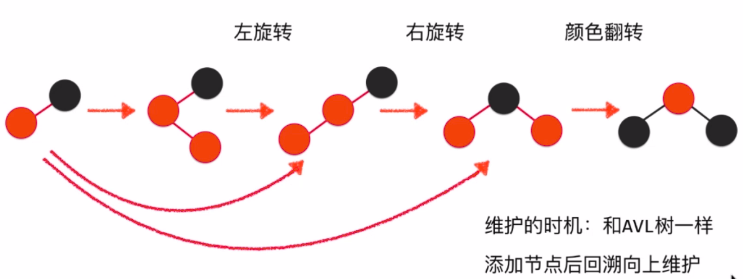
- 永远添加红色节点
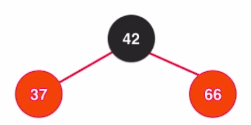
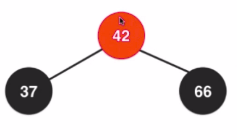
- 颜色的翻转
step1:
step2:
step3:
- 右旋转
step1:
step2:
step3:
step4:
- 左旋转(类似右旋转)
- 总体流程
- 本质:多个键值对
- 通过哈希函数将"键"转换为"索引"
- 复杂度为O(1)
- 整型
- 小范围的正整数直接使用
- 小范围的负整数进行偏移 -100
100----> 0200 - 大整数
- 通常做法:取模
- 一个简单的通用的解决办法:模一个素数
- 浮点型
- 在计算机中都是32位或64位的二进制表示
- 所以可以将浮点数转成整型处理
- 字符串
- 转成整型处理
- 设计原则
- 一致性: 如果a==b,则hash(a) == hash(b)
- 高效性: 计算高效便捷
- 均匀性: 哈希值均匀分布
-
链地址法
- 注:TreeMap的底层实现就是红黑树
- 总共有M个地址
- 如果放入哈希表的元素为N
- 如果每个地址是链表: O(N/M)
- 如果每个地址是平衡树: O(log(N/M))
- 改进:
- 和静态数组一样
- 固定地址空间是不合理的
- 需要resize
- 设计:
- 平均每个地址承载的元素多过一定的程度,即扩容--> N / M >= upperTol
- 平均每个地址承载的元素少过一定的程度,即缩容--> N / M < lowerTol
- 平均复杂度O(1)
- 每个操作在O(lowerTol) ~ O(upperTol)
- 扩容后续问题
- 扩容会是M = 2 * M,即M不再是素数了
- 参考方案,引入常量素数数组
- 哈希表:均摊复杂度为O(1),牺牲了什么? 顺序性
-
开放地址法
- 每一个地址都对添加的元素进行开放,只是必须按照规则进行添加
- 采用开放地址法的检测方式
- 线性探测法: 每次+1进行探测
- 平方探测法: +1 +4 +9 +16...
- 二次哈希
- 再哈希法: 当一个哈希函数产生的索引冲突,就使用另外一个哈希函数产生索引
- 即当发生冲突时就将添加在冲突元素后面的第一个空
- 有序的集合和有序的映射
- 平衡树: AVL树,红黑树,即标准库中的TreeMap和TreeSet
- 无序的集合和无序的映射
- 哈希表
- 线性结构
- 动态数组
- 普通队列
- 栈
- 链表
- 哈希表(开放地址法)
- 树形结构
- 二叉树:
- 二分搜索树
- AVL树: 破坏平衡时以旋转方式进行维护
- 红黑树: 以2-3树的结构进行维护;统计性能更高
- 堆
- 线段树
- 多叉树:
- Trie
- 并查集
- 二叉树:
- 图结构
- 邻接表
- 邻接矩阵
- 抽象数据结构
- 线性表: 动态数组,链表
- 栈,队列
- 集合,映射
- 有序集合,有序映射
- 无序集合,无序映射