P2D_model

LIONSIMBA provides a simulation environment for Li-ion cells. The specific modelling approach lies on the so-called electrochemical pseudo two-dimensional (P2D) model which is represented by means of Partial Differential and Algebraic Equations (PDAEs).

In this section a brief description of numerical approach used to implement the P2D model is provided.

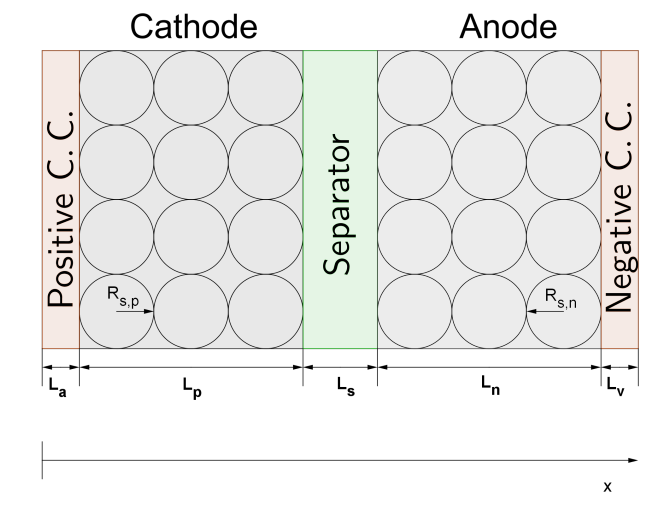
As shown in the figure below, the Li-ion cell is composed of five main sections: the positive current collector (a), the cathode (p), the separator (s), the anode (n), and the negative current collector (v). The index $z \in \{a, p, s, n,v\}$ is used to indicate the different sections. The thickness of each battery section is defined by $L_z$ and $L:=\sum_{z}L_z$ represents the overall battery thickness. The electrodes and the porous separator of the Li-ion cell are placed in contact with an electrolyte solution, facilitating the flow of ions during charging and discharging processes. During a charging process, the ions deintercalate from the positive electrode and, passing through the porous media of the separator, intercalate into the negative electrode. The inverse process occurs when discharging the cell. li_ion The diffusion of ions within the electrodes are modeled by

$\frac{\partial}{\partial t} c_s^{*}(x,t) - c_s^{\textrm{avg}}(x,t) = - \frac{R_s}{5 D_{\textrm{eff}}^s} j(x,t)$

where $t \in \mathbb{R}^{+}$ represents the time, $x \in \mathbb{R}$ is the one-dimensional spatial variable, $c_s^{*}(x,t)$ and $c_s^{\textrm{avg}}(x,t)$ are the surface and average concentration of solid particles respectively, the function $j(x,t)$ represents the ionic flux, and $R_s$ and $D_{\textrm{eff}}^{s}$ account for the particle radius and effective diffusion coefficients of the solid phases. The bulk State of Charge (SOC) of the anode is defined as

$\textrm{SOC}(t) := \frac{1}{L_n\,c_s^{\textrm{max,n}}}\,\int_{0}^{L_n} c_s^{\textrm{avg}}(x,t)\,dx,$

where $c_s^{\textrm{max,n}}$ represents the maximum concentration of Li-ions in the negative electrode. The flow of ions inside the electrolyte solution is modeled by a diffusion equation,

$\epsilon \frac{\partial}{\partial t}c_e(x,t) = \frac{\partial}{\partial x} \left[ D_{\textrm{eff}} \frac{\partial c_e(x,t)}{\partial x}\right] a (1-t_{plus}) j(x,t),$

where $c_{e}(x,t)$ represents the electrolyte concentration of ions, $t_{plus}$ defines the transference number, $a$ is the particle surface area to volume ratio, $D_{\textrm{eff}}$ accounts for the effective diffusion coefficients in the electrolyte, and $\epsilon$ represents the material porosity. According to Ohm's law, the conservation of charge in the electrodes can be defined as

$\frac{\partial}{\partial x}\left[\sigma_{\textrm{eff}} \frac{\partial}{\partial x} \Phi_{s}(x,t) \right] = a F j(x,t),$

where $\Phi_s(x,t)$ is the solid potential, $\sigma_{\textrm{eff}}$ is the electrodes effective conductivity, and $F$ is the Faraday's constant. The potential of the Li-ion cell is obtained as

$V_{\textrm{out}}(t) := \Phi_s(0,t) - \Phi_s(L,t).$

Similarly, a modified Ohm's law is used to represent the charge conservation within the electrolyte:

$aFj(x,t) = -\dfrac{\partial}{\partial x}\left[\kappa_{\textrm{eff}} \frac{\partial}{\partial x}\Phi_{e}(x,t) \right] + \dfrac{\partial}{\partial x}\left[\dfrac{2 \kappa_{\textrm{eff}} \textrm{R} T(x,t)}{F}(1-t_{plusx})\frac{\partial}{\partial x}\ln c_e(x,t) \right]$

where $\Phi_e(x,t)$ is the electrolyte potential, $T(x,t)$ represents the temperature, $\textrm{R}$ defines the universal gas constant, and $\kappa_{\textrm{eff}}$ is the effective conductivity of the liquid phase. The temperature dynamics are modeled by an energy balance,

$\rho C_p \frac{\partial}{\partial t} T(x,t) = \frac{\partial}{\partial x}\left[ \lambda \frac{\partial}{\partial x} T(x,t)\right] + Q_{\textrm{ohm}}(x,t) + Q_{\textrm{rxn}}(x,t) + Q_{\textrm{rev}}(x,t),$

where $\rho$ is the material density, $C_p$ is the specific heat, $\lambda$ is the heat diffusion coefficient, and the terms $Q_{\textrm{ohm}}(x,t)$ , $Q_{\textrm{rev}}(x,t)$ , and $Q_{\textrm{rxn}}(x,t)$ account for ohmic, reversible, and reaction heat sources as shown in Kumaresan et.al, 2008.

The above equations are coupled by means of the ionic flux, which is defined by the Butler-Volmer equation

$j_{\textrm{int}}(x,t) = 2 \frac{i_{0,\textrm{int}}}{F} \sinh \left[\frac{0.5 F}{\textrm{R} T(x,t)} \eta_{\textrm{int}}\right],$

where the exchange current density is given by

$i_{0,\textrm{int}}= F k_{\textrm{eff}} \sqrt{c_e(x,t)(c_s^{\textrm{max}}-c_s^*(x,t))c_s^*(x,t)}.$

The overpotential at the anode side is defined as

$\eta_{\textrm{int}} := \Phi_s(x,t) - \Phi_e(x,t) - U_n,$

while at the cathode side as

$\eta_{\textrm{int}} := \Phi_s(x,t) - \Phi_e(x,t) - U_p$

where the terms $U_p$ and $U_n$ represent the cathode and anode OCV respectively, and $k_{\textrm{eff}}$ represents the effective kinetic reaction rate. The intercalation flux $j_{\textrm{int}}(x,t)$ is zero inside the separator.

A more detailed explanation of the model, parameters and its numerical implementation are give in the related LIONSIMBA article.

Copyright (C) - LIONSIMBA - Lithium-ION SIMulation BAttery Toolbox

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

P2D_model

Clone this wiki locally