Create readme.md

2024/LSD/readme.md

@@ -0,0 +1,53 @@
+# Read Notes: LSDs for Neuron Segmentation
+
+Here are linshey's Read Notes for <Sheridan, A., Nguyen, T.M., Deb, D. *et al.* (2023): Local shape descriptors for neuron segmentation[^1]>.
+
+## Auxiliary-Task Learning
+
+A major challenge in neuron segmentation is the paucity of labeled data. Auxiliary-Task Learning (ATL) has emerged as a promising technique to address this challenge, which improves the generalization of target tasks by leveraging the useful signals provided by some related auxiliary tasks (which is label-accessible and simple to train)[^2]. For example, single-image depth estimation can be utilized as ATL for semantic segmentation[^3].
+
+Given the target task $\mathcal{T}_{\mathrm{tgt}}$ and the auxiliary task $\mathcal{T}_{\mathrm{aux}}$, then the objective is to optimize[^2]:
+$$
+\min_{\theta} 
+\mathbb{E}_{\mathcal{T}_{\mathrm{tgt}}}\mathcal{L}_{\mathrm{tgt}}(\theta)+
+\lambda\mathbb{E}_{\mathcal{T}_{\mathrm{aux}}}\mathcal{L}_{\mathrm{aux}}(\theta)
+$$
+The hyper parameter $\theta$ is critical to control the gradient/distribution of $\mathcal{T}_{\mathrm{tgt}}$ and $\mathcal{T}_{\mathrm{aux}}$ in appropriate relationship, and to avoid gradient conflicts and negative transfer[^2].
+
+In this article[^1], the auxiliary learning task is to predict Local Shape Descriptors (LSDs), a $\mathbb{R}^{10}$ vector denoting some local object statistics. For every voxel $v$, let $S_v$ be a subset of voxels $\{v'|\mathrm{InTheSameSegment}(v,v')\and |v-v'|<\sigma\}$. The $\mathrm{lsd}(v)\in \mathbb{R}^{10}$ is defined as [the size of $S_v$, the offset between $v$ and the mean coordinates of $S_v$, the covariance of $S_v$].
+
+An interesting fact is that the conventional ATL architecture in LSDs paper, MtLSD, in which LSDs and nearest neighbor affinities are output in one pass, does not work well. The best-performance network architecture AcRLSD are auto-context setup in which the LSDs from one U-net are fed into a second U-net to produce the affinities.[^1]
+
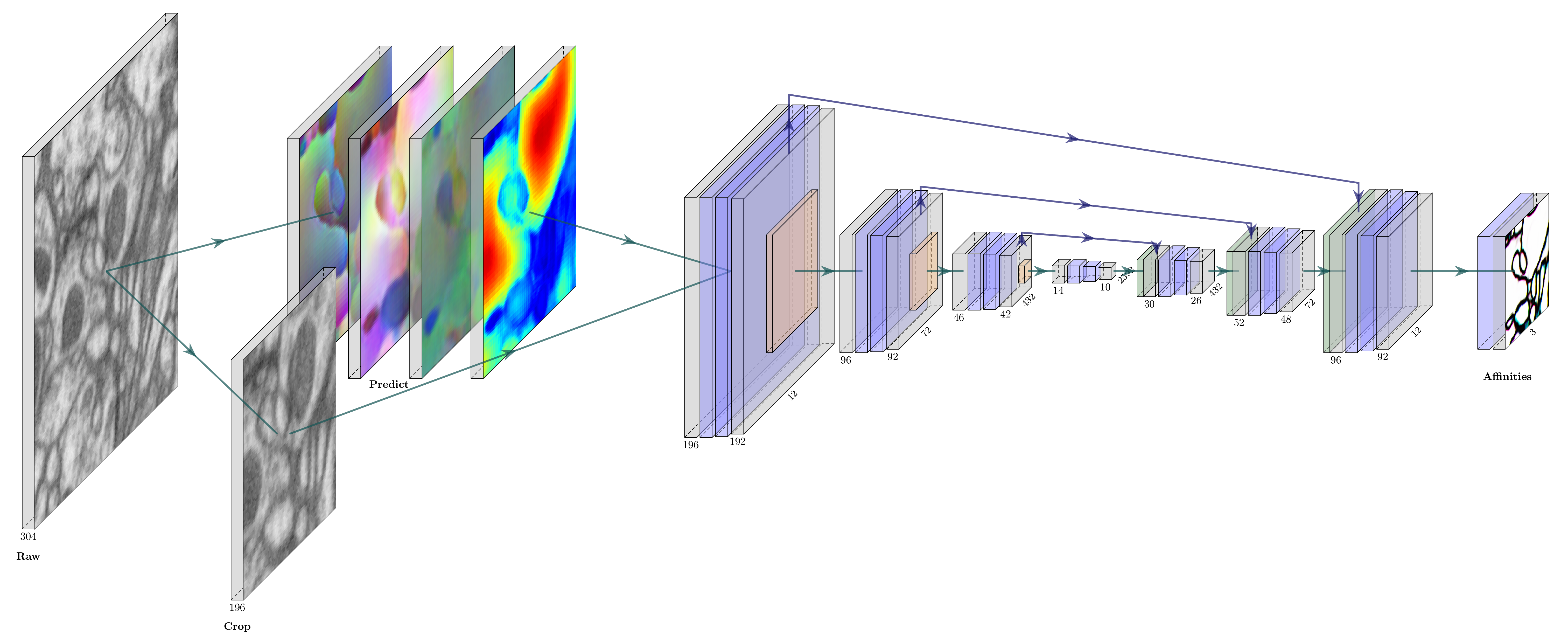+![![img](https://localshapedescriptors.github.io/assets/img/acrlsd.png)](https://localshapedescriptors.github.io/assets/img/lsd.png)
+
+![img](https://localshapedescriptors.github.io/assets/img/acrlsd.png)
+
+## 3D U-net
+
+Intuitively, 3D U-net is quite easy to understand, as you can simply imagine a U-net, in which planar input is replaced by 3D input, and `conv2d` is replaced by `conv3d`. So 3D U-net is a network for volumetric segmentation that learns from sparsely annotated volumetric images and generates dense segmentation.[^3]It is suitable for tasks of sample scarcity due to good generalization performance. The network structure of 3D U-net has nothing special than a up-dimension version of U-net. Here are two figures from 3D U-Net paper.[^4]
+
+<img src="C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20241124165731318.png" width = "500" alt="fig.2" align=center /><img src="C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20241124170218020.png" width = "500" alt="fig.2" align=center />
+
+## Post Processing
+
+How to reconstruct the neurons after receiving affinities from 3D U-net? Funke *et al* (2019)[^5]proposes a solution combining watershed and agglomeration which is also adopted by LSDs.[^1]
+
+First, extract fragments running a watershed algorithm on the predicted affinities. The fragments are then represented in a region adjacency graph (RAG), where edges are scored to reflect the predicted affinities between adjacent fragments: edges with small scores will be merged before edges with high scores.[^5] (Note: fragment is called supervoxel in LSDs paper).
+
+![image-20241124195054260](C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20241124195054260.png)
+
+So the reconstruction of neuron is a 2-stage process, prediction of affinities, post processing (such as, watershed + agglomeration). The optimization of the reconstruction process can be categorized by this thinking:
+
+1. To optimize the prediction of affinities, such as applying 3D U-net[^6], introducing ATL task for U-net[^1] and Dense Voxel Embeddings[^7].
+2. To optimize the training target of prediction network so as to better satisfy the need of post processing, such as utilization of MALIS loss[^5] and min-cut metric[^1].
+3. To optimize the the merging of fragments. This part is closely correlated to topology, parallelization and computer graphics.
+
+## Refs
+
+[^1]: Sheridan, A., Nguyen, T.M., Deb, D. *et al.* (2023). Local shape descriptors for neuron segmentation. *Nat Methods* **20**, 295–303 . https://doi.org/10.1038/s41592-022-01711-z
+[^2]: Jiang, J., Chen, B., Pan, J., Wang, X., Dapeng, L., Jiang, J., & Long, M. (2023). ForkMerge: Mitigating Negative Transfer in Auxiliary-Task Learning. https://arxiv.org/abs/2301.12618
+[^3]: Liebel, L., & Körner, M. (2018). Auxiliary Tasks in Multi-task Learning. https://arxiv.org/abs/1805.06334
+[^4]: Çiçek, Ö., Abdulkadir, A., Lienkamp, S. S., Brox, T., & Ronneberger, O. (2016). 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. https://arxiv.org/abs/1606.06650
+[^5]: Funke, J., Tschopp, F., Grisaitis, W., Sheridan, A., Singh, C., Saalfeld, S., & Turaga, S. C. (2019). Large Scale Image Segmentation with Structured Loss Based Deep Learning for Connectome Reconstruction. IEEE Transactions on Pattern Analysis and Machine Intelligence, 41(7), 1669–1680. https://doi.org/10.1109/TPAMI.2018.2835450
+[^6]: Lee, K., Zung, J., Li, P., Jain, V., & Seung, H. S. (2017). Superhuman Accuracy on the SNEMI3D Connectomics Challenge. https://arxiv.org/abs/1706.00120
+[^7]: Lee K, Lu R, Luther K, Seung HS. (2021). Learning and Segmenting Dense Voxel Embeddings for 3D Neuron Reconstruction. IEEE Trans Med Imaging. https://pmc.ncbi.nlm.nih.gov/articles/PMC8692755/