Algorithms and Data Structures

Written in Python, Golang, Node and Java

Vin Colgin (Summer/Fall 2019)

https://github.com/marvincolgin

https://linkedin.com/in/mcolgin

Table of Contents:

• Algorithms
  • Bubble Sort
  • Insertion Sort
  • Merge Sort
  • Quick Sort
• Data Structures
  • Arrays
    • Reverse Elements
    • Insert and Shift Array Elements
    • Binary Search
  • Singly Linked Lists
  • Stack (LIFO)
    • Balanced Brackets
  • Queue (FIFO)
    • Queue: Animal Shelter
  • Binary Tree (BT)
    • Breadth-first Traversal
    • Find the Maximum Value
    • FizzBuzzTree
    • Tree Intersection
  • Binary Search Tree (BST)
  • Hash Table
    • Repeated Words
    • Left Join
  • Graphs
    • Get Graph Edges
    • Depth-First Traversal

CI/CD

CircleCi for Tests:

Algorithms

Bubble Sort

Source Code:

Python

Source: Github

def bubble_sort(arr):
    # BigO == n^2

---

Insertion Sort

Source Code:

Python

Source: Github

def insertion_sort(arr):
    # BigO = O(2n)

---

Merge Sort

Source Code:

Python

Source: Github

def merge_sort(arr):
    # BigO (n log n)
    # :: log n, as this is a divide algo
    # :: n, as we need to merge the halfs back

def merge_split(arr):
    # actual merge_sort function, without error handling
    # :: recursivily called

def merge_array(arr, left, right):
    # combine left and right sides

---

Quick Sort

Source Code:

Python

Source: Github

def quick_sort(arr):
    # BigO (n log n)
    # :: log n, as this is a divide algo
    # :: n, as we need to merge the halfs back

Data Structures

Arrays

In Python, arrays are dynamic lists of pointers to memory addresses, Big O Time == 0(1)

Reverse Elements

Create a function, which reverses an array/linked-list, as passed via a parameter and pass the new array back as the return() for the function.

Approach & Efficiency My initial approach was to utilize the list.insert() and list.pop() to rebuild the list in reverse order. However, my white boarding partner showed me a more pythonic method utilizing slices with a -1 stride.

Solution Two solutions were used, one that utilizes a while() loop and is destructive on the inbound array. The second is "pythonic" and utilizes an index slice and a -1 stride.

Whiteboard

Source Code:

Python

Source: Github

def reverse_array(orig):
def reverse_array2(orig):

---

Insert and Shift Array Elements

Write a function which takes in an array and the value to be added. Without utilizing any of the built-in methods available to your language, return an array with the new value added at the middle index.

Solution Create an index into the array where the value will be inserted, utilize slice and .append/.extend to construct a return array

Whiteboard

Source Code:

Python

Source: Github

def insert_shift_array_sorted(arr, val):
def insert_shift_array(arr, val):

---

Binary Search

Write a function which takes in an array and the value to be searched. Return -1 if the value is not found, otherwise return the index (0 based). Incoming array is sorted.

Solution Divide and Conquer! Look at the middle element, is it the middle element? Return. If not, create a new middle from either the smaller side or larger side. Repeat.

Whiteboard

Source Code:

Python

Source: Github

def array_binary_search(arr, val):

---

Singly Linked Lists

Linked-Lists (singly) are dynamic data-structures which resembles a length of chain, where the entire length of chain is the list and the individual links of the chain are nodes. A singlarly linked list is only traversable in one direction, but utilizing a head element that points to the first node in the list, the second node in the list points to the next link in the chain, and finally the last element in the list points to "none"

Whiteboard

Insert()

KthFromEnd(): Iterative Approach

KthFromEnd(): Recursive Approach

MergeList()

Source Code:

Python

Source: Github

class LinkList()

    def __init__(self):
        # constructor

    def toJSON(self):
        # dump object to JSON and return as String

    def insert(self, value):
        # insert value at the head of the list

    def includes(self, value):
        # traverse list and determine if a value exists
        # return bool

    def count(self):
        # count the number of nodes and return count

    def append(value):
        # adds a new node with the given value to the end of the list
        # BigO == O(n)

    def insertBefore(value, newVal):
        # add a new node with the given newValue immediately before the first value node
        # BigO == O(n)

    def insertAfter(value, newVal):
        # add a new node with the given newValue immediately after the first value node
        # BigO == O(n)

class ListNode()
    def __init__(self, value, next=None, prev=None):
         # constructor

Golang

Source: Github

type LinkNode struct {
    value interface{}
	next  *LinkNode
	prev  *LinkNode
}
func (node *LinkNode) Init(value interface{}) {
    head *LinkNode
	// @TODO: comparison_func func
}

type LinkList struct {
	head *LinkNode
	// @TODO: comparison_func func
}
func (list *LinkList) Init() {}
func (list *LinkList) toJSON() string {}
func (list *LinkList) toStr() string {}
func (list *LinkList) Insert(value interface{}) bool {}
func (list *LinkList) Includes(value interface{}) bool {}
func (list *LinkList) Get(value interface{}) interface{} {}
func (list *LinkList) Count() int {}
func (list *LinkList) Append(value interface{}) bool {}
func (list *LinkList) Remove(value interface{}) bool {}
func (list *LinkList) Peek() (bool, interface{}) {}
func (list *LinkList) InsertBefore(targetVal, newVal interface{}, afterInstead bool) bool {}
func (list *LinkList) InsertAfter(targetVal, newVal interface{}) bool {}
func (list *LinkList) KthFromEnd(k int) (bool, interface{}) {}
func (list *LinkList) MergeList(listA, listB LinkList) LinkList {}

Node

Source: Github

// LinkNode this is the internal object for individual link-nodes
class LinkNode {
	constructor(value) {
}

// LinkList is the internal data-structure
class LinkList {
	constructor() {}

   toStr() {}
   count() {}
   peek() {}
   append(value) {}
   insert(value) {}
   includes(value) {}
   remove(value) {}
   insertBefore(targetVal, newVal, afterInstead=false)  {}
   insertAfter(targetVal, newVal) {}
   kthFromEnd(k) {}
   mergeList(listA, listB) { }

Java

Source: Github

public class LinkList {

   public class RetObj {}

   public Node head;

   private BiFunction<String, String, Boolean> comparisonFunc;
   public void setComparisonFunc(BiFunction f) {}

   public LinkList(BiFunction cf) {}

   class Node {}

   public void insert(String value) {}
   public int count() {}
   public Boolean includes(String value) {}
   public RetObj peek() {}
   public String toStr() {}
   public Boolean append(String value) {}
   public Boolean remove(String value) {}
   public String get(String value) {}
   private Boolean insertBeforeOrAfter(String targetVal, String newVal, Boolean afterInstead) {}
   public Boolean insertBefore(String targetVal, String newVal) {}
   public Boolean insertAfter(String targetVal, String newVal) {}
   public void traverse(Consumer actionFunc) {}
   public String kthFromEnd(int k) {}
   public LinkList mergeList(LinkList listA, LinkList listB) {}
}

---

Stack (LIFO)

Source Code:

Python

Source: Github

class Stack():
    def push(val) -> bool:
    def pop() -> str:
    def peek() -> str:

Golang

Source: Github

type Stack struct {
	_data linklist.LinkList
}
func (stack *Stack) Init() {}
func (stack *Stack) Count() int {}
func (stack *Stack) Pop() (bool, interface{}) {}
func (stack *Stack) Push(val interface{}) bool {}
func (stack *Stack) Peek() (bool, interface{}) {}

Node

Source: Github

// Stack implementation of LIFO
class Stack {
   constructor() {}
   count() {}
   pop() {}
   push(val) {}
   peek() {)
}

Java

Source: Github

public class Stack {
   private LinkList _data = null;

   public Stack() {}
   public int count() {}
   public Boolean push(String val) {}
   public String pop() {}
   public LinkList.RetObj peek() {}
   public String toStr() {}
}

---

Balanced Brackets

Create a function, which takes in a string and tests it to make sure that any open brackets ('{','(','[') are balanced with their corresponding closing-brackets ('}',')',']').

Whiteboard

Source Code:

Python

Source: Github

def multi_bracket_validation(input : str) -> boolean:

---

Queue (FIFO)

Whiteboard

Source Code:

Python (queue)

Source: Github

class Queue():

    def enqueue(val) -> bool:
        # Add a value to the queue

    def dequeue(val) -> bool:
        # Remove entry from queue with a given value

    def peek() -> str:
        # Get value from the head of the queue (without removing it)

Python (stack)

Source: Github

class PseudoQueue(object):

    def __init__(self):
        # create Stack for internal data-struct

    def count(self):
        # pass through method to underlying data struct
        # BigO == O(n)

    def enqueue(self, val: str) -> bool:
        # enqeue a value at the end queue
        # BigO == O(1)

    def dequeue(self) -> (str, bool):
        # dequeue from head of queue
        # BigO == O(n)
        # Algo: use a second stack, as we need the bottom element on the first stack
        # so we are going to unload the first stack, into a temp stack, in order to
        # get at the bottom element of the first, then rebuild it from temp to first-stack

Node

Source: Github

class Queue {
   constructor() {}
   count() {}
   toStr() {}
   enqueue(val) {}
   dequeue(val) {}
   peek() {}

Golang

Source: Github

// Queue implementation of LIFO
type Queue struct {
	_data linklist.LinkList
}

// Init inistantiate the stuct
func (queue *Queue) Init() {}

// Count the number of items in linklist
func (queue *Queue) Count() int {}

// ToStr return the Queue as a String
func (queue *Queue) ToStr() string {}

// Enqueue to add a value to the queue
func (queue *Queue) Enqueue(val interface{}) bool {}

// Dequeue to remove a specific value from the Qeueue
func (queue *Queue) Dequeue(val interface{}) bool {}

// Peek at the front value in the Queue
func (queue *Queue) Peek() (bool, interface{}) {}

Java

Source: Github

public class Queue {
   private LinkList _data = null;

   public Queue() {}
   public int count() {}
   public Boolean enqueue(String val) {}
   public Boolean dequeue(String val) {}
   public LinkList.RetObj peek() {}
   public String toStr() {}
}

---

Queue: Animal Shelter

create a class called AnimalShelter which holds only dogs/cats. The shelter operates as first-in / first-out

Whiteboard

Source Code:

Python

Source: Github

class AnimalType(IntEnum):

class Animal(object):

    def __init__(self, animaltype : AnimalType):
        # create internal data structs

    def serialize(self):
        # return json for obj

    def Factory(jsonstr : str): # -> Animal
        # create Animal class Dog|Cat for Json

class Cat(Animal):
    def __init__(self):
        # create internal data structs

class Dog(Animal):
    def __init__(self):
        # create internal data structs

class AnimalShelter():
    def __init__(self):
        # create internal data structs

    def enqueue(self, animal : Animal):
        # add animal to shelter

    def dequeue(self, pref : AnimalType=None) -> Animal:
        # grab animal that has been in queue the longest, optionally provide parameter

---

Binary Tree (BT)

Source Code:

Python

Source: Github

class TraverseMethod(IntEnum):
    # enum class for traversal and processing order

class Node:
    # class for nodes within Tree

    def __init__(self, value):
        # constructor for creating Node

class BinaryTree:

    def __init__(self):
        # constructor for creating BinaryTree

    def traverse(self, method : TraverseMethod, action_func):
        # visit each node in atree, using a specified method and call action_func() for each node

        def _visit(node):
            # recusive function for visiting each node

    def returnAsArr(self, method : TraverseMethod):
        # return the enter tree as an array using a specified method

Node

Source: Github

// enum class for traversal and processing order
var TraverseMethod = {
   PRE_ORDER: 1,
   IN_ORDER: 2,
   POST_ORDER: 3
}

// enum class for comparisons, gt, lt and equal
var ComparisonSign = {
    LESS: 1,
    GREATER: 2,
    EQUAL: 3
}

// class for nodes within Tree
class Node {
   constructor(value) {
      this.value = value
      this.left = null
      this.right = null
   }
}

// BinaryTree Implementation
class BinaryTree {
   constructor() {}
   traverse(method, action_func) { }
   returnAsArr(method) {}
}

class BinarySearchTree extends BinaryTree {
   constructor(comparison_func=null) { }
   comparison_func_default(val1, val2, CS) {}
   add(new_value) {}
   contains(target_value) {}
}

---

Breadth-first Traversal

Breadth first traversal method which takes a Binary Tree as its unique input.

Whiteboard

Source Code:

Python

Source: Github

def breadth_first(tree, action_func):

---

Find the Maximum Value

Function called find_maximum_value which takes binary tree as its only input

Whiteboard

Source Code:

Python

Source: Github

def find_max(tree : BinaryTree) -> (bool,int):

---

FizzBuzzTree

Write a function called FizzBuzzTree which takes a tree as an argument. Determine weather or not the value of each node is divisible by 3, 5 or both, and change the value of each of the nodes:

• value is divisible by 3, replace the value with "Fizz"
• value is divisible by 5, replace the value with "Buzz"
• value is divisible by 3 and 5, replace the value with "FizzBuzz"
• Return the tree with its new values.

Whiteboard

Source Code:

Python

Source: Github

def fizzBuzzTree(tree: BinaryTree) -> BinaryTree:
    # traverse tree, value = value%3==0 ? 'Fizz, value = value%5==0 ? 'Buzz' (set value to 'FizzBuzz' if both conditions met)

---

Tree Intersection

tree_intersection(): given two binary-trees, return an array containing shared values

Whiteboard

Source Code:

Python

Source: Github

def tree_intersection(tree1, tree2: BinaryTree) -> list:
    # return an array with all the values in both tree1 and tree2
    # BigO Time==O(2n)  Space==0(1.3n) 30% for hashtable
    # assumption: No Duplicates within Trees

---

Binary Search Tree (BST)

Source Code:

Python

Source: Github

class BinarySearchTree(BinaryTree):
    # class for binary-search-tree

    def add(self, new_value):
        # adds new value to the tree

        def _find_and_insert(node):
            # recursive method for evaluating a node and calling itself depending on the value

    def contains(self, target_value) -> bool:
        # accepts a value, and returns a boolean indicating whether or not the value is in the tree at least once.

        def _visit(node):
            # recursive function for isiting each node

---

Hash Table

Source Code:

Python

Source: Github

class HashTable():

    def __init__(self, hashtableSize = 1024):
        # create with hashTableSize

    def _makePayload(self, name, value):
        # return dict of name/value pair

    def _makeHash(self, name) -> int:
        # create a hash based on the name to be added to hashtable
        # this is a silly hash, as it's just for experiment and
        # gives us the ability to easily create collisions. Live
        # code should use something more sophisticated

    def _getHashIndex(self, hash: int) -> int:
        # get the index into the hash-table for a given hash value

    def _hashtable_compare_func(self, payload1, payload2) -> bool:
        # func passed to LinkList compare

    def add(self, name, value):
        # accepts name/value pair and adds them to the hashtable
        # if there are collisions, then they will be handled
        # by using a linked-list

    def get(self, name):
        # returns value in hashtable for a given name
        # if the value is not found, and exception will be raised

    def contains(self, name) -> bool:
        # returns true|false if the name is in the hashtable

---

Repeated Words

repeated_words(): search the longstr for complete words, return the first word that has more than one occurrence

Whiteboard

Source Code:

Python

Source: Github

def repeated_word(longstr: str) -> str:
    # search the longstr for complete words
    # return the first word that has more than
    # one occurrence
    # BigO Time==O(n) Space==O(n*1.3)

---

Left Join

left_join(): given two hash-tables, return a list of all items from the first h1 and the value that exists in h2, if no value exists return None

• LEFT JOINs two hashmaps into a single data structure.
• 1st param is hashmap with words and synonyms
• 2nd param is hashmap with words and antonyms
• Combine the key and corresponding values (if they exist) into a new data structure according to LEFT JOIN logic.
• Code Styling: PEP8

Whiteboard

Source Code:

Python

Source: Github

def left_join(h1, h2: HashTable) -> list:
    # perform a left-join on h1 against h2
    # - returns a list of dict:{word,syntonym,antonym)
    # - BigO time==O(n) space==0(n)
    # -      worst: time==O(3n)

---

Graphs

Source Code:

Python

Source: Github

class Vertex:
    def __init__(self, value: Any):

class Edge:
    def __init__(self, vertex: Vertex, weight=0):

class Graph:
    def __init__(self):
    def __len__(self) -> int:
    def add_vertex(self, value) -> Vertex:
    def add_edge(self, vert1: Vertex, vert2: Vertex, weight=0.0):
    def get_neighbors(self, vertex: Vertex) -> List[Edge]:
    def get_vertexes(self) -> Optional[List[Vertex]]:
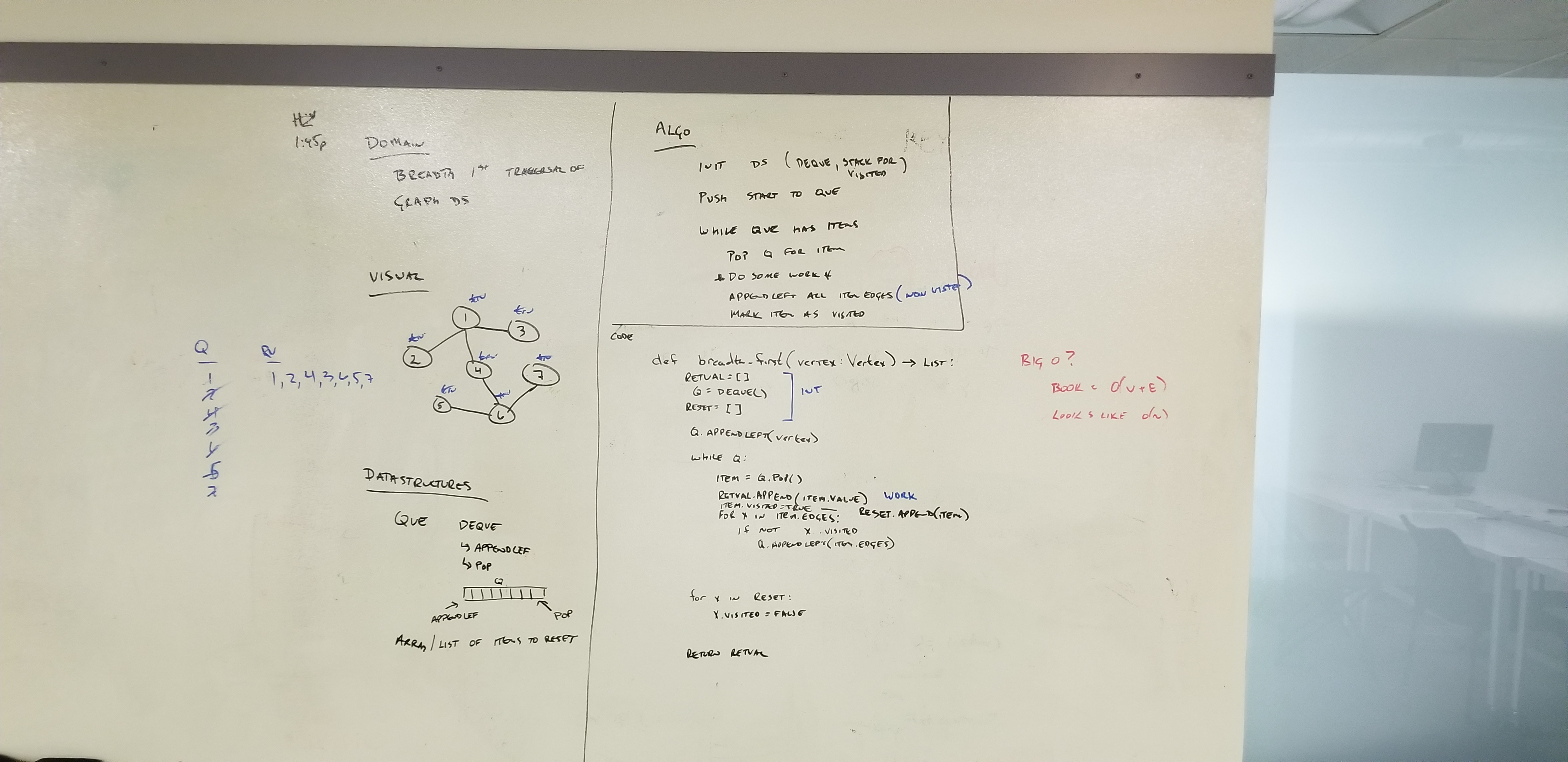
    def breadth_first(self, root, action_func):

---

Get Graph Edges

Overall: Identify if a given path exists through the Graph where path is a given list of values Use Case: Given a complete Graph data-structure, containing a variety of Vertexes/Edges containing city-names and costs, (Flight Routes) and a list of cities (Flight Plan), return True|False if the flight-plan can be performed and the cost.

Whiteboard

Source Code:

Python

Source: Github

def get_edges(graph: Graph, path_ro: List) -> Tuple[bool, float]:
    # identify if a given path exists through the Graph
    # where path is a given list of values
    # @path_ro will be treated as read-only
    # BigO time==O(V+P*E) .. where p is len(path_ro)
    # BigO space==O(1)

---

Depth-First Traversal

• breadth first traversal method which takes a Binary Tree as its unique input.
• print every node encountered

Whiteboard

Source Code:

Python

Source: Github

def depth_first_recursive(self, root: Vertex, action_func: Any) -> None:
def depth_first(self, root: Vertex, action_func: Any) -> None: