2. Specifications
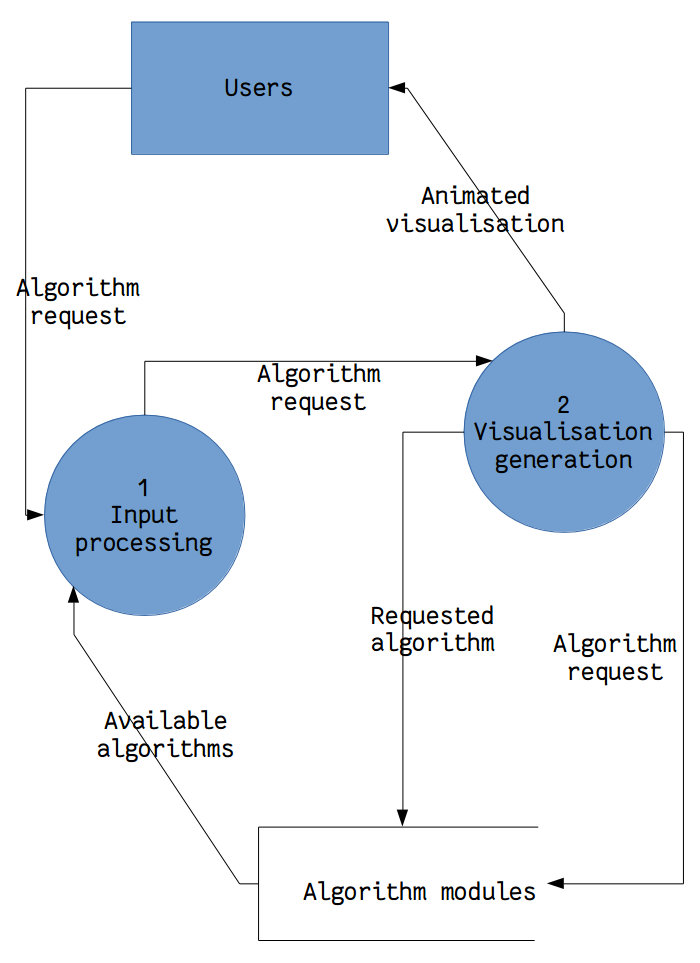
Source files for diagrams can be found by cloning the full wiki repository, or directly from here.
resources/specs/diag-dfdlv0.png
| Input | Process | Output |
|---|---|---|
| Requested Algorithm | Located required module with requested algorithm | |
| Data to sort, view settings | Generate visual elements | Unsorted visual elements |
| Sort command | Sort visual elements | Sorted visual elements |
| Identifier | Type | Size | Description | Example |
|---|---|---|---|---|
| Visualizations | Array of Strings | 256 | List of possible visualizations as a constant | [“Bogosort”, “Bogobogosort”, “Quicksort”] |
| Visualization | String | 256 | Selected visualization | “Bogobogosort” |
| Inputs | Array of Integers or Strings | 256 | Array to be sorted in the visualization, determined by type of user-provided | [0, 21, 42, 4, 3, 6, 9, 33 ] |
| IsAscending | Boolean | 2 | Whether or not to sort in ascending order | True |
All examples sort in ascending order, and are all code snippets from established algorithms.
FOR i = 1 TO LEN(List) - 1
j = i
WHILE j > 0 AND List[j - 1] > List[i] DO
List[j] = List[j - 1]
j -= 1
END WHILE
List[j] = List[i][3]
NEXT
FOR i = 0 TO LEN(List) - 1
SWAP(List[i], List[INDEXOF(MIN(List from i to LEN(List)))])
NEXT
SUB MergeSort(List)
Left = {}
Right = {}
Middle = LEN(List) / 2
FOR EACH i IN List BEFORE Middle
ADD i to Left
FOR EACH i IN List AFTER OR EQUAL Middle
ADD i to Right
Left = MergeSort(Left)
Right = MergeSort(Right)
RETURN MERGE(Left, Right)
END SUB
# Build the heap in array a so that largest value is at the root
HEAPIFY(List, LEN(List))
# The following loop maintains the invariants that List[0:end] is a heap and every element
# beyond end is greater than everything before it (so List[end:LEN(List)] is in sorted order)
End = LEN(List) - 1
WHILE End > 0 DO
# List[0] is the root and largest value. The swap moves it in front of the sorted elements.
SWAP(List[End], List[0])
# the heap size is reduced by one
End -= 1
# the swap ruined the heap property, so restore it
SIFTDOWN(List, 0, End)
SUB Quicksort(List, Lo, Hi)
# Lo is the index of the leftmost element of the subarray
# Hi is the index of the rightmost element of the subarray (inclusive)
IF Lo < Hi THEN
PivotIndex = ChoosePivot(List, Lo, Hi)
PivotValue = List[PivotIndex]
# put the chosen pivot at List[Hi]
SWAP(List[PivotIndex], List[Hi])
StoreIndex = Low
# Compare remaining array elements against PivotValue = List[Hi]
FOR i = Lo TO Hi−1 THEN
IF List[i] < PivotValue THEN
SWAP(List[i], List[StoreIndex])
StoreIndex += 1
END IF
NEXT
SWAP(List[StoreIndex], List[Hi]) # Move pivot to its final place
END IF
Quicksort(List, Lo, StoreIndex - 1)
Quicksort(List, StoreIndex + 1, Hi)
END SUB
n = LEN(List)
REPEAT UNTIL n = 0
NewN = 0
FOR i = 1 TO n-1 DO
IF List[i-1] > List[i] THEN
SWAP(List[i-1], List[i])
NewN = i
END IF
END FOR
n = NewN
LOOP
Gaps = [701, 301, 132, 57, 23, 10, 4, 1] # Marcin Ciura’s gap sequence
# Start with the largest gap and work down to a gap of 1
FOR EACH Gap IN Gaps
# Do a gapped insertion sort for this gap size.
# The first gap elements List[0..Gap-1] are already in gapped order
# keep adding one more element until the entire array is gap sorted
FOR i = gap TO LEN(List) - 1 DO
# add List[i] to the elements that have been gap sorted
# save List[i] in temp and make a hole at position i
Temp = List[i]
# shift earlier gap-sorted elements up until correct location is found
j = i
WHILE j >= Gap AND List[j - Gap] > Temp DO
List[j] = List[j - Gap]
j -= Gap
END WHILE
# put temp (the original List[i]) in its correct location
List[j] = Temp
NEXT
NEXT
Gap = LEN(List)
Shrink = 1.3
REPEAT UNTIL Gap = 1 AND NOT Swapped
# update the gap value for a next comb
Gap = Gap DIV Shrink
IF Gap < 1 THEN
Gap = 1 # minimum gap is 1
END IF
i = 0
Swapped = False
# a single "comb" over the input list
REPEAT UNTIL i + Gap > LEN(List)
IF List[i] > List[i+Gap] THEN
SWAP(List[i], List[i+gap])
Swapped = True
END IF
i += 1
LOOP
LOOP
Count = Array of length LEN(List) with all values 0
Output = Array of length LEN(List)
# calculate the histogram of key frequencies:
FOR Item IN List DO
Count[INDEXOF(Item)] += 1
NEXT
# calculate the starting index for each key:
Total = 0
FOR i = 0 TO LEN(List) DO
OldCount = Count[i]
Count[i] = Total
Total += OldCount
NEXT
# copy to output array, preserving order of Lists with equal keys:
FOR EACH Item IN List DO
Output[Count[KEY(Item)]] = Item
Count[KEY(Item)] += 1
NEXT
# put items into buckets
FUNCTION SignificantBits(x, k) # returns k most significant bits of x
RETURN FLOOR(x/2^LEN(x)-k)
END FUNCTION
Buckets = Array of LEN(List) empty lists
FOR i = 0 TO LEN(List) - 1 DO
INSERT List[i] into Buckets[SignificantBits(List[i], k)]
NEXT
# sort each individual bucket with an arbitrary sorting function
# can be sorted with BucketSort itself, and if so, becomes a kind of Radix sort
FOR i = 0 TO LEN(List) - 1 DO
SORT(Buckets[i])
NEXT
RETURN concatenation of buckets[0], ...., buckets[n-1]
WHILE List is not sorted
SHUFFLE(List)
END WHILE
i = 1
WHILE i != Length of List DO
IF List is not sorted THEN i = 1 # reset if not sorted
IF List[Items 0 to i] are not sorted THEN SHUFFLE(List[Items 0 to i])
END FOR
SUB StoogeSort(List)
IF List[0] < List[LEN(List) - 1] THEN
SWAP(List[0], List[LEN(List)-1])
END IF
IF Length of List >= 3 THEN
ThirdMark = LEN(List) - 3
StoogeSort(List from 0 to ThirdMark) # first third of list
StoogeSort(List from ThirdMark to LEN(List)) # last 2/3 of list
StoogeSort(List from 0 to ThirdMark) # first third of list
END IF
RETURN List
END SUB
Wireframe prototypes for the initial webapp interface are reproduced below. A minimal style is going to be taken, with information summed up in a simple and compact way allowing for fewer required pages. Source files for the wireframes can be found by cloning the wiki, or by downloading the OpenOffice Draw source files from here.
