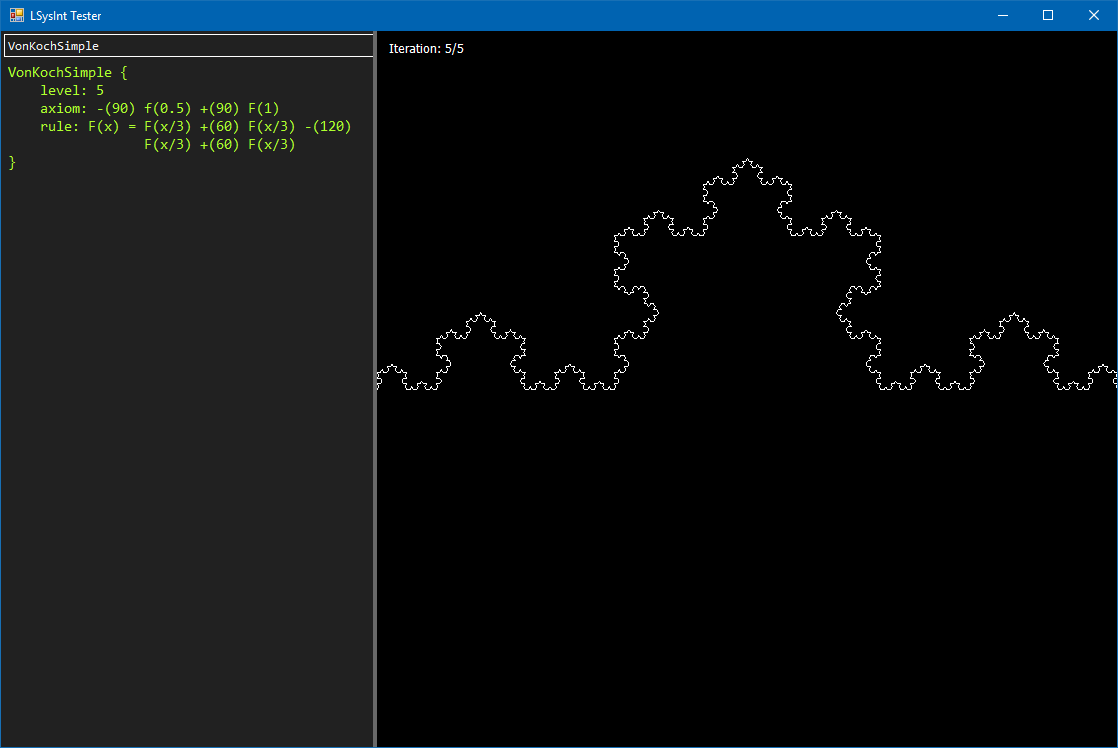
A simple L-System parser, interpreter and renderer, written in VB.NET
This is, in fact, a very rough and simple interpreter to render L-system formulas.
The grammar is very similar to that of the more mature project LILiS, with a few distinctions:
- A curve is defined using a name with its body enclosed between curly brackets.
- Parameters names must always end with a colon.
- So far, only eigth parameters are supported:
- level: indicates the maximum recursion level
- axiom: indicates the initial conditions
- rule: indicates one or more rules to be applied to the axiom
- angle: defines the default angle when none is specified
- offsetX: defines a rendering origin offset in the horizontal direction
- offsetY: defines a rendering origin offset in the vertical direction
- length: defines the default length of a segment when none is specified
- constant: defines a simple string-based substitution (no function support yet)
- Although LSysInt does not currently support "definitions", most of the time these can be represented through one or more rules.
- These are the currently supported internal functions:
- F(x): move forward and draw
xamount of pixels - B(x): move backwards and draw
xamount of pixels - f(x): move forward
xamount of pixels - +(x): increase the angle by
xamount - -(x): decrease the angle by
xamount - [: save current vector state
- ]: restore saved vector state
- %(r, g, b, a): set vector color
- F(x): move forward and draw
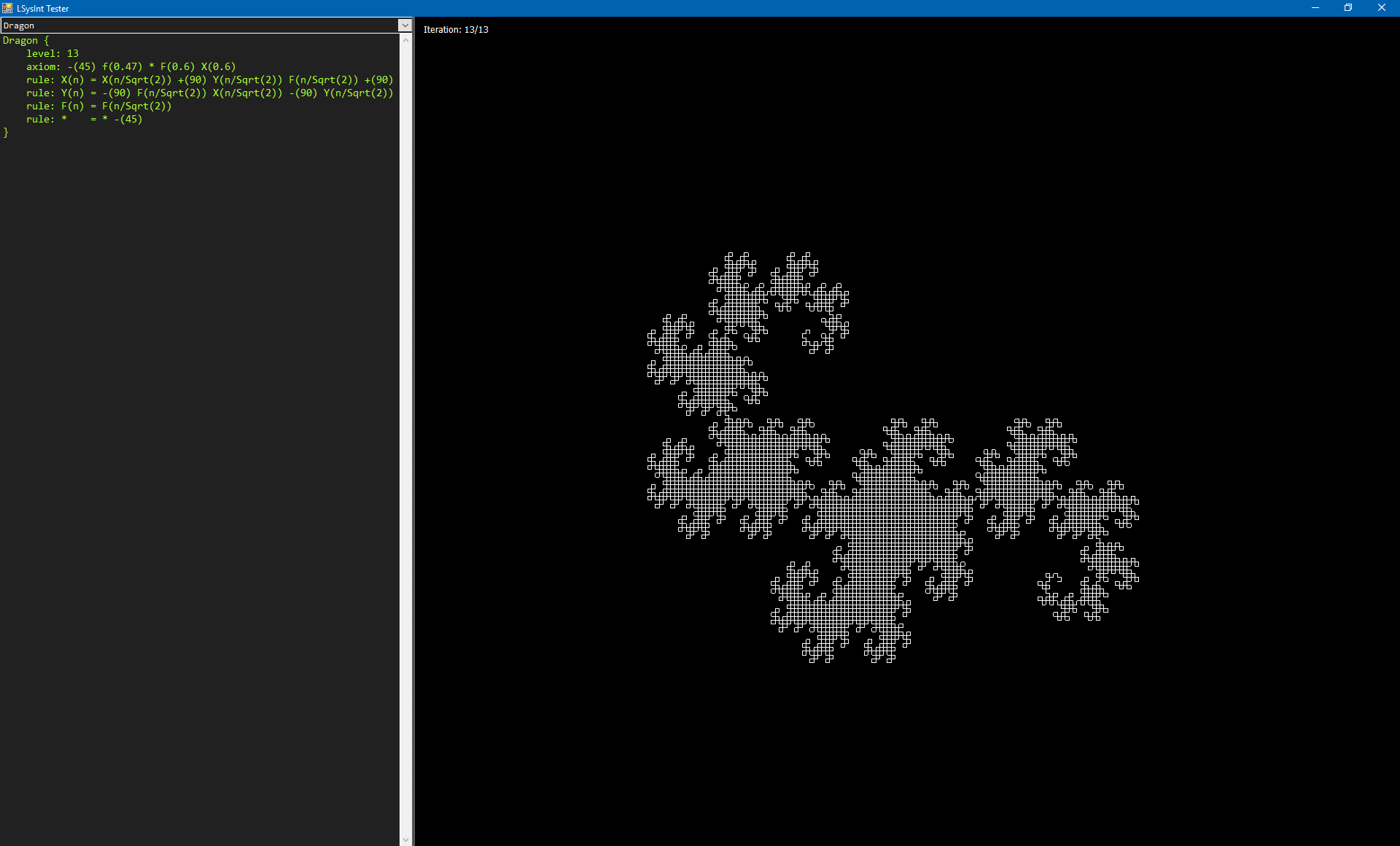
Here's a sample code to render the dragon curve up to its 13th iteration:
Dragon {
level: 13
axiom: -(45) f(0.47) * F(0.6) X(0.6)
rule: X(n) = X(n/Sqrt(2)) +(90) Y(n/Sqrt(2)) F(n/Sqrt(2)) +(90)
rule: Y(n) = -(90) F(n/Sqrt(2)) X(n/Sqrt(2)) -(90) Y(n/Sqrt(2))
rule: F(n) = F(n/Sqrt(2))
rule: * = * -(45)
}