DistMesh is a simple Julia code for automatic generation of unstructured 2D triangular and 3D tetrahedral volume meshes using (level set) distance functions for describing geometries and domains.
This repository is a Julia port of the consolidated 2D/3D DistMesh implementation for MATLAB and Octave.
 |
 |
 |
The original DistMesh MATLAB algorithm was invented by Per-Olof Persson and Gilbert Strang in the Department of Mathematics at MIT. More detailed descriptions of the DistMesh algorithm and the original MATLAB mesh generation code can be found in the SIAM Review paper and other references linked below.
The simplicity of the DistMesh algorithm is due to using signed distance functions (level sets) to specify and describe domains, geometries, and regions to mesh. Distance functions specify the shortest distance from any point in space to the boundary of the domain, where the sign of the function is positive outside the region, negative inside, and zero on the boundary. This definition is used to identify if a point is located in or outside of the geometry. Moreover, the gradient of the distance function points in the direction of the boundary, allowing points outside to be efficiently moved back to the domain.
A simple example is the unit circle in two dimensions, which has the distance function d(r) = r-1, where r = sqrt(x^2+y^2) is the distance from the origin. For more complicated geometries the distance function can be computed by interpolation between values on a grid, which is a common representation for level set methods.
For the mesh generation procedure, DistMesh uses the Delaunay triangulation routine in the VornoiDelaunay Julia module and tries to optimize the node locations by a force-based smoothing procedure. The topology is regularly updated by Delaunay. The boundary points are only allowed to move tangentially to the boundary by projections using the distance function. This iterative procedure typically results in very uniform and well-shaped high quality meshes.
To use the this mesh generation code, simply download the stand alone distmesh source code and run it in Julia (tested under Julia v6.2). The function syntax is as follows
(P, T, STAT) = DISTMESH( FD, FH, H0, BBOX, P_FIX, E_FIX, IT_MAX, FID)
where FD is a function handle to the geometry description that
should take evaluation coordinates and points as input. For example
fd = p -> sqrt.(sum(p.^2,2)) - 1 specifies the distance
function for a unit circle (both function handles, string function
names, and anonymous functions are supported). Similar to FD, FH
a function describing the desired relative mesh size distribution. For
example fh = p -> ones(size(p,1),1) specifies a uniform
distribution where FH evaluates to 1 at all points. H0 is a
numeric scalar specifying the initial edge lengths, and BBOX is a
2 by 2 in 2D (or 2 by 3 in 3D) bounding box of the domain (enclosing
the zero contour/level set of FD). P_FIX optionally specifies a
number of points that should always be present (fixed) in the
resulting mesh. E_FIX can be sets of edge vertex indices to
constrain, or alternatively a cell array with function handle to call.
IT_MAX sets the maximum number of grid generation iterations
allowed (default 1000). Finally, FID specifies a file
identifies for output (default 1 = terminal output).
The DistMesh-Julia function returns the grid point vertices in P, triangulated simplices in T, as well as an optional statistics struct STAT including timings and convergence information.
Input:
FD: Distance function d(x,y,(z))
FH: Scaled edge length function h(x,y,(z))
H0: Initial edge length
BBOX: Bounding box [xmin ymin (zmin); xmax,ymax,(zmax)]
P_FIX: Fixed node positions [N_P_FIX x 2/3]
E_FIX: Constrained edges [N_E_FIX x 2]
IT_MAX: Maximum number of iterations
FID: Output file id number (default 1 = terminal)
Output:
P: Grid vertex/node coordinates [N_P x 2/3]
T: Triangle indices [N_T x 3]
STAT: Mesh generation statistics (struct)
To automatically run the collection of basic mesh generation examples described below, type distmesh_demo into the Julia command prompt from the directory where the distmesh files can be found.
-
Example 1: (Uniform mesh on unit circle)
fd = p -> sqrt.(sum(p.^2,2)) - 1 fh = p -> ones(size(p,1)) (p, t) = distmesh( fd, fh, 0.1, [-1 -1;1 1] ) plotgrid( p, t ) -
Example 2: (Uniform mesh on ellipse)
fd = p -> p[:,1].^2/2^2 + p[:,2].^2/1^2 - 1 fh = p -> ones(size(p,1)) (p, t) = distmesh( fd, fh, 0.2, [-2 -1;2 1], [], [], 200 ) plotgrid( p, t ) -
Example 3: (Uniform mesh on unit square)
fd = p -> -minimum([minimum([minimum([p[:,2] 1-p[:,2]],2) p[:,1]],2) 1-p[:,1]],2) fh = p -> ones(size(p,1)) (p, t) = distmesh( fd, fh, 0.2, [-1 -1;1 1], [-1 -1;-1 1;1 -1;1 1] ) plotgrid( p, t ) -
Example 4: (Uniform mesh on complex polygon)
pv = [-0.4 -0.5;0.4 -0.2;0.4 -0.7;1.5 -0.4;0.9 0.1; 1.6 0.8;0.5 0.5;0.2 1;0.1 0.4;-0.7 0.7;-0.4 -0.5] fd = p -> dpolygon( p, pv ) fh = p -> ones(size(p,1)) (p, t) = distmesh( fd, fh, 0.1, [-1 -1;2 1], pv ) plotgrid( p, t ) -
Example 5: (Rectangle with circular hole, refined at circle boundary)
fd = p -> maximum( [dpolygon(p,[-1 -1;1 -1;1 1;-1 1;-1 -1]) -(sqrt.(sum(p.^2,2))-0.5)], 2 ) fh = p -> 0.05 + 0.3*(sqrt.(sum(p.^2,2))-0.5) plotgrid( p, t ) -
Example 6: (Square, with size function point and line sources)
dcircle = (p,xc,yc,r) -> sqrt.((p[:,1]-xc).^2+(p[:,2]-yc).^2)-r fd = p -> -minimum([minimum([minimum([p[:,2] 1-p[:,2]],2) p[:,1]],2) 1-p[:,1]],2) fh = p -> minimum([minimum(hcat(0.01+0.3*abs.(dcircle(p,0,0,0)), 0.025+0.3*abs.(dpolygon(p,[0.3 0.7;0.7 0.5;0.3 0.7]))),2) 0.15*ones(size(p,1),1)],2) (p, t) = distmesh( fd, fh, 0.01, [0 0;1 1], [0 0;1 0;0 1;1 1] ) plotgrid( p, t ) -
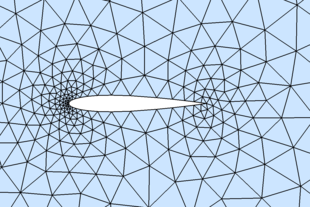
Example 7: (NACA0012 airfoil)
hlead = 0.01; htrail = 0.04; hmax = 2; circx = 2; circr = 4 a = 0.12/0.2*[0.2969 -0.126 -0.3516 0.2843 -0.1036] dcircle = (p,xc,yc,r) -> sqrt.((p[:,1]-xc).^2+(p[:,2]-yc).^2)-r fd = p -> maximum(hcat( dcircle(p,circx,0,circr), -((abs.(p[:,2])-polyval([a[5:-1:2];0],p[:,1])).^2-a[1]^2*p[:,1]) ), 2 ) fh = p -> minimum([minimum([hlead+0.3*dcircle(p,0,0,0) htrail+0.3*dcircle(p,1,0,0)],2) hmax*ones(size(p,1),1)],2) fixx = 1 - htrail*cumsum(1.3.^(0:4)') fixy = a[1]*sqrt.(fixx) + polyval([a[5:-1:2];0],fixx) pfix = [[circx+[-1 1 0 0]*circr; 0 0 circr*[-1 1]]'; 0 0; 1 0; fixx' fixy'; fixx' -fixy'] bbox = [circx-circr -circr; circx+circr circr] h0 = minimum([hlead htrail hmax]) (p, t) = distmesh( fd, fh, h0, bbox, pfix ) plotgrid( p, t ) -
Example 8: (Uniform mesh on unit sphere)
fd = p -> sqrt.(sum(p.^2,2)) - 1 fh = p -> ones(size(p,1),1) (p,t) = distmesh( fd, fh, 0.2, [-1 -1 -1;1 1 1] ) plotgrid( p, t ) -
Example 9: (Uniform mesh on unit cube)
fd = p -> -minimum([minimum([minimum([minimum([minimum([p[:,3] 1-p[:,3]],2) p[:,2]],2) 1-p[:,2]],2) p[:,1]],2) 1-p[:,1]],2) fh = p -> ones(size(p,1),1) pfix = [-1 -1 -1;-1 1 -1;1 -1 -1;1 1 -1; -1 -1 1;-1 1 1;1 -1 1;1 1 1] (p,t) = distmesh( fd, fh, 0.2, [-1 -1 -1;1 1 1], pfix ) plotgrid( p, t ) -
Example 10: (Uniform mesh on cylinder)
fd = p -> -minimum([minimum([p[:,3] 4-p[:,3]],2) 1-sqrt.(sum(p[:,1:2].^2,2))],2) fh = p -> ones(size(p,1),1) pfix = [-1 -1 -1;-1 1 -1;1 -1 -1;1 1 -1; -1 -1 1;-1 1 1;1 -1 1;1 1 1] (p,t) = distmesh( fd, fh, 0.5, [-1 -1 0;1 1 4] ) plotgrid( p, t )
- VornoiDelaunay.jl
- Plots.jl
-
3D is technically supported by DistMesh-Julia, but Julia is missing a 3D Delaunay triangulation functionality.
-
Proper module bundling not implemented.
[3] P.-O. Persson's DistMesh website
[4] Consolidated 2D/3D DistMesh for MATLAB and Octave
[5] libDistMesh - A Simple Mesh Generator in C++
[6] PyDistMesh - A Simple Mesh Generator in Python
[7] Mesh generator - Java implementation of DistMesh
[8] DistMesh - Wolfram Language Implementation
[9] J. Burkardt's DistMesh repository
[10] KOKO Mesh Generator
The DistMesh-Julia code is copyrighted by J.S. Hysing and Precise Simulation Limited and licensed under the GNU GPL License; see the License and Copyright notice for more information.