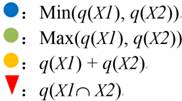Geodetector

A note for understanding and review the great work of geodetector, some paragraphs and figures are copied directly from original file. Source: Wang JF-{Geodetector}

Define

Spatial Stratified Heterogeneity (SSH) refers to the difference within strata less than between strata. Such as landuse types and climate zones in spatial data, seasons and years in time series, occupations, age groups, incomes strata.

SSH occurs in all scales from universe to DNA.

Tasks

All tasks can be accomplished by the Geodetector q-statistic

where N and σ2 stand for the number of units and the variance of Y in study area, respectively;

Geodetector: measure SSH and to make attribution for/by SSH (Fig. 1)

1. measure and find SSH among data;
2. test the coupling between two variables Y and X, according to their SSHs, without assumption of linearity of the association;
3. investigate interaction between two explanatory variables X1 and X2 to a response variable Y, without any specific form of interaction such as the assumed product in econometrics (Fig. 2).

Interpretation of q value (Fig.1).

The value of q is strictly within [0, 1].

1. If Y is stratified by Y itself:

• q = 0 indicates that Y is absent of SH
• q = 1 indicates that Y is SH perfectly
• 100q% measures the degree of SH of Y.

2. If Y is stratified by an explanatory variable X

• then q = 0 indicates that there is no coupling between Y and X
• q = 1 indicates that Y is completely determined by X
• X explains 100q% of Y.

q-statistic measures the association between X and Y (or X1 and X2), both linearly and nonlinearly.

Geodetector q statistic helps understand spatial confounding, sample bias and overfitting.

1. Confounding arises if a global model was applied to a SH population, leading to statistical insignificance. The problem can be simply avoided if SH is identified (by Geodetector q statistic) then modelling in the strata, separately.
2. A sample would be biased if a population is SH and the sample do not cover all strata. The problem can be solved if SH is identified (by Geodetector q statistic) then apply bias remedy models such as Heckman regression and Bshade method.
3. Local models aim to overcome heterogeneity but often suffer overfitting and too many parameters to interpret. The problems can be avoided if modelling in strats or stratifying the outputs of a local model then interpreting the stratified parameters.

Functions of Geodetector:

1. The risk detector maps response variable in strata: Y(X);
2. The factor detector q-statistic measures the degree of SH of a variable Y; and the determinant power of an explanatory variable X of Y;
3. The ecological detector identifies the difference of the impacts on Y between two explanatory variables X1 ~ X2;
4. The interaction detector reveals whether the risk factors X1 and X2 (and more X) have an interactive influence on a response variable Y (Fig.2).

Tutorial of Geodetector

Note: Y is numerical; X MUST be categorical, e.g. landuse types, seasons. If X is numerical it should be transformed to be categorical, e.g. GDP per capita is stratified into 5 strata

script

1. R package: {geodetector}
2. R package: {GD}
3. Excel file: (http://www.geodetector.cn/#_Download,_with_Datasets_1)

output

Geodetector output 4 files:

1. risk detector
2. factor detector
3. ecological detector
4. interaction detector.

1.Risk detector

The results of each environmental risk factor are presented in two table:

1. The first table gives the average Y in each stratum of a risk factor.
2. The second table gives the statistically significant difference in the average Y between two strata of X; if there is a significant difference, the corresponding value is “Y”, else it is “N”.

2.Factos detector

Present the each environmental risk factor's q values and p values.

3.Ecological detector

Present the statistically significant differences between two environmental risk factors. If Y(X1) (risk factor names in row) was significantly bigger than Y(X2) (risk factor names in column), the associated value is “Y”, while “N” expresses the opposite meaning.

4.Interaction detector

“Interaction relationships” represent the interaction relationship for the two factors. The relationship is defined in a coordinate axis. It has 5 intervals, including

• “( -∞，min(q(x), q(y)) )”
• “( min(q(x), q(y)), max(q(x), q(y)) )”
• “( max(q(x), q(y)), q(x) + q(y) )”
• “ q(x) + q(y) ”
• “( q(x) + q(y), +∞ )”

The interaction relationship is determined by the location of q(xÇy) in the 5 intervals.

FAQs

Q1. How to make a partition (stratification; classification) for a variable x?

1. If x is categorical, e.g. landuse types, do nothing;
2. If x is numerical

• Stratification according to some industry consensus, e.g. UN standard for the GDP per capita: poor, middle, …; or
• Ordered then equally divided 2~7 strata. Use the stratification with bigger q and interpretable; or
• Try different stratifications, use the one with biggest q. The philosophy like regression (OLS), in which try different {b} and use the one maximizing R2.

Q2. Will stratification vary with variables?

Yes, like regression in which coefficient b value varies with variables;

Q3. Software reports error or abnormal result

Numerical x has to be stratified (see Q1), no less than 2 sample units in each stratum.

Q4. When p value should be reported?

1. When measuring SSH of a variable y: 100q% SSH degree, at p sig. level
2. When attributing y to x: x explains 100q% of y, no need to report p value.

Q5. Should Sqi = 1? where i stands for i-th variable

No, because of nonlinear coupling between y and xi; or interaction between xi. For example, U shape association between human mortality (y) and temperature (x)

Q6. Direction of q?

No directions for nonlinearity, e.g. Kuznets curve; U shape association between human mortality (y) and temperature (x). But, you may check linear direction in each of strata.

Q7. Big sample, say a remote sensing image composed by 1024´1024 pixels

1. Resampling, 100 sample units in each of strata are usually enough
2. Use R-Geodetector software