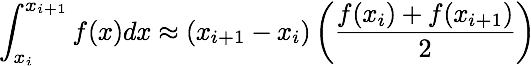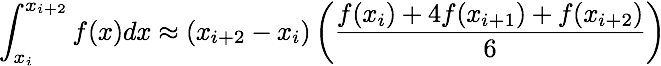In Homework #3 we will write come OpenMP code to numerically evaluate integrals using various integration algorithms.
Repository layout:
-
homework3/:Python wrapper of your C library. The functions defined here allow you to use your C code from within Python. The test suite calls these functions which, in turn, call your C functions. DO NOT MODIFY. Any modifications will be ignored / overwritten when the homework is submitted.
Please read the docstrings in this file to see how to call the wrapper and what kind of information is expected to be returned. Compare with the signature of the underlying C function.
-
include/:The library headers containing (1) the C function prototypes and (2) the C function documentation. Document your C functions here.
-
lib/:The compiled C code will be placed here as a shared object library named
libhomework3.so. -
report/:Place your
report.pdfhere. See the "Report" section below. -
src/:C library source files. This is where you will provide the bodies of the corresponding functions requested below.
Do not change the way in which these functions are called. Doing so will break the Python wrappers located in
homework3/wrappers.py. You may, however, write as many helper functions as you need.Aside from writing your own tests and performing computations for your report, everything you need to write for this homework will be put in the files here.
-
ctests/:Directory in which to place any optional C code used to debug and test your library as well as practice compiling and linking C code. See the file
ctests/example.cfor more information and on how to compile. -
Makefile: See "Compiling and Testing" below. -
test_homework3.py: A sample test suite for your own testing purposes.
The makefile for this homework assignment has been provided for you. It will
compile the source code located in src/ and create a shared object library
lib/libhomework3.so. You can also use this Makefile to compile all of the
scripts you write in the directory, ctests.
Run,
$ make lib
to create lib/libhomework3.so. This library must exist in order for the Python
wrappers to work. As a shortcut, running
$ make test
will perform
$ make lib
$ python test_homework3.py
Run,
$ make example.out
to compile the script ctests/example.c into an executable called
example.out. Copy the syntax of the corresponding make command if you would
like to write more C scripts.
In this assignment we will implement several numerical integration techniques in serial and in parallel. Given a function, f, and some x-data points, form the arrays
x = [x_0, x_1, ..., x_{N-1}]
fvals = [f(x_0), f(x_1), ..., f(x_{N-1})]
Using these data one can approximate the integral of f from x_0 to x_{N-1}
using the following formulae
Scipy has built-in functions
scipy.linalg.trapz
and
scipy.linalg.simps
which, given an x-data set and function evaluations, will use these rules to
estimate the integral. For example,
>>> from numpy import linspace, sin, pi
>>> from sicpy.integrate import trapz, simps
>>> x = linspace(-1,pi,8) # eight, equally-spaced points between -1 and pi
>>> fvals = sin(x)
>>> integral_trapz = trapz(fvals, x)
>>> integral_simps = simps(fvals, x, even='first') # see simps documentationIn this assignment we will write serial and parallel versions of these algorithms. Additionally, we will perform some parameter tuning on our parallel implementation of Simpson's rule. In particular, you are to provide the definitons of the below functions.
In each of these functions, fvals is a length N array of function
evaluations of type double on the elements of x, a length N array of
domain points of type double. These are fed in from either Python via Numpy
arrays or your test scripts in the directory ctests.
-
double trapz_serial(double* fvals, double* x, int N)Approximates the integral of f using the trapezoidal rule.
-
double trapz_parallel(double* fvals, double* x, int N, int num_threads)Approximates the integral of f using the trapezoidal rule in parallel. The number of threads to be used should be an argument to the function.
-
double simps_serial(double* fvals, double* x, int N)Approximates the integral of f using Simpson's rule. Note that there are two cases to consider: the "nice" case when
Nis odd and the "not nice" case whenNis even. Once you understand why there is an issue in theNis even case resolve the issue by taking a single trapezoidal rule approximation at the end of the data array to capture the "missing" part of the integral.(Hint: read the
scipy.linalg.simpsdocumentation. In particular, read about theevenkeyword.) -
double simps_parallel(double* fvals, double* x, int N, int num_threads)Approximates the integral of f using the trapezoidal rule in parallel. The number of threads to be used should be an argument to the function.
-
double simps_parallel_chunked(double* fvals, double* x, int N, int num_threads, int chunk_size)Approximates the integral of f using the trapezoidal rule in parallel. The number of threads to be used should be an argument to the function. In this implemenation you should use a
#pragma omp forconstruct so you can pass in a chunk size to the loop thread scheduler. (Or write one manually. See Lecture 11 and 12.)You do not need to use
#pragma omp forin your implementation ofsimps_parallelbut you may if you want to.
Your implementations will be run through the following test suite. Tests will
use an x where distance betweeen subsequent points, x[i+1]-x[i], is not
necessarily uniform.
trapz Tests:
- (1pt) Check the definition of
trapz_serialusing data arrays of length two. - (1pt) Test if
trapz_serialmatches (up to close to machine precision) the output ofscipy.integrate.trapzfor variousN. - (1pt) Check the definition of
trapz_parallelusing data arrays of length two. - (1pt) Test if
trapz_parallelmatches (up to close to machine precision) the output ofscipy.integrate.trapzfor variousN.
simps Tests:
- (1pt) Check the definition of
simps_serialusing data arrays of length three. - (1pt) Test if
simps_serialmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNodd. (This is the "nice" case.) - (1pt) Test if
simps_serialmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNeven. (This is the "not nice" case where an extra trapezoidal rule approximation needs to be done at the end of the data. See thescipy.linalg.simpsdocumentation.) - (1pt) Check the definition of
simps_parallelusing data arrays of length three. - (1pt) Test if
simps_parallelmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNodd. - (1pt) Test if
simps_parallelmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNeven.
Chunked simps Tests:
- (1pt) Check the definition of
simps_parallel_chunkedusing data arrays of length three. - (1pt) Test if
simps_parallel_chunkedmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNodd and various values ofchunk_size. - (1pt) Test if
simps_parallel_chunkedmatches (up to close to machine precision) the output ofscipy.integrate.simpsfor variousNeven and various values ofchunk_size.
Total: (13 / 13pts)
Note that in this homework assignment we will manually verify that the
parallel versions of your algorithms indeed implement some sort of parallel
structure. You will recieve zero points on the parallel tests if you only
implement the serial version of the code.
Produce a PDF document named report.pdf in the directory report of the
repository. Please write your name and UW NetID (e.g. "cswiercz", not your
student ID number) at the top of the document. The report should contain
responses to the following questions:
-
(12/20) Create a plot of parallel loop chunk sizes vs. corresponding runtime using chunked parallel Simpson's method. In particular, create a
semilogxplot of timings ofsimps_parallel_chunkedwith chunk size on horizontal axis and runtime on the vertical axis, usinghomework3.time_simps_parallel_chunkedwith the following data:N = 2**20 x = numpy.linspace(-1,3,N) y = sin(exp(x)) chunk_sizes = [2**0, 2**2, 2**4, 2**6, 2**8, ..., 2**20]- (2pt) In black, timings with
num_threads = 1. - (2pt) In green, timings with
num_threads = 2. - (2pt) In blue, timings with
num_threads = 4. - (2pt) In red, timings
num_threads = 8. - (2pt) Plot uses a logarithmic scale on the x-axis.
- (1pt) Both x- and y-axes are labeled appropriately.
- (1pt) Plot has a meaningful title.
Note that you may want to start with a smaller value of
Nwhile you're experimenting with getting the plot just right. Also, try generating several versions of the plot in case there is some system noise causing erradic timing behavior. - (2pt) In black, timings with
-
(8/20) Let's analyze this plot. In particular, provide comments on the following questions.
- (2pt) What can be attributed to the
nthreads = 8behavior when thechunk_sizeis small? - (2pt) What happens when the
chunk_sizeis equal to the problem size (i.e. whenchunk_size = 2**20 = N) and why does this affect the timings in the way that the plot suggests? - (2pt) Why is
chunk_sizerelevant to this implementation of Simpson's rule as opposed to the simple example we did in class during Lecture 12? (5 May, 2016?) - (2pt) What range of chunk values appear to be optimal for this particular
value of
Nin parallel Simpson? Can you conjecture an ideal chunk value as a function ofN. If so, why? If not, why not? Note that this "optimal" chunk size may not be the same for non-Simpson's rule problems.
- (2pt) What can be attributed to the
Provide documentation for the function prototypes listed in all of the files in
include following the formatting described in the
Grading document.
We will time your implementation of the function simps_parallel via the
function time_simps_parallel with num_threads = 4 for some value N between
1e7 and 1e18.
N = # approximately 1e7 and approximately 1e18
x = numpy.linspace(-1,3,N)
y = sin(exp(x))