-
Notifications
You must be signed in to change notification settings - Fork 30
Lorenz equations
The Lorenz' equations system [1] is a non linear system of pure ODEs that retains a reasonable-complex behaviour: such a system, for a certain parameters-region exhibits a chaotic dynamics useful for testing FOODIE solvers.
The Lorenz' ODEs system can be written as:
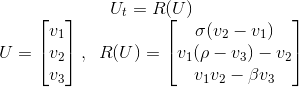
The parameters set is constant and it is here selected as:
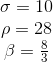
These values are chaos-inducing thus they magnify the eventual numerical inaccuracies of FOODIE solvers, see [2].
[1] Deterministic Nonperiodic Flow, Lorenz E.N., Journal of the Atmospheric Sciences, 1963, vol. 20, pp. 130--141, doi: http://dx.doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
[2] Scientific software design: the object-oriented way, Rouson, Damian, Jim Xia, and Xiaofeng Xu, Cambridge University Press, 2011
Before apply a FOODIE solver for solving the above system the system itself must be defined accordingly to FOODIE's type_integrand abstract type (upon which each FOODIE's solver is based).
The proposed FOODIE-compatible Lorenz' system definition is:
type, extends(integrand) :: lorenz
!< Lorenz equations field.
!<
!< It is a FOODIE integrand class.
private
integer(I_P) :: dims=0 !< Space dimensions.
integer(I_P) :: steps=0 !< Number of time steps stored.
real(R_P), dimension(:,:), allocatable :: state !< Solution vector, [1:state_dims,1:time_steps_stored].
real(R_P) :: sigma=0._R_P !< Lorenz \(\sigma\).
real(R_P) :: rho=0._R_P !< Lorenz \(\rho\).
real(R_P) :: beta=0._R_P !< Lorenz \(\beta\).
contains
! auxiliary methods
procedure, pass(self), public :: init !< Init field.
procedure, pass(self), public :: output !< Extract Lorenz field.
! type_integrand deferred methods
procedure, pass(self), public :: t => dLorenz_dt !< Time derivate, resiuduals function.
procedure, pass(self), public :: update_previous_steps !< Update previous time steps.
procedure, pass(lhs), public :: integrand_multiply_integrand => lorenz_multiply_lorenz !< Lorenz * lorenz operator.
procedure, pass(lhs), public :: integrand_multiply_real => lorenz_multiply_real !< Lorenz * real operator.
procedure, pass(rhs), public :: real_multiply_integrand => real_multiply_lorenz !< Real * Lorenz operator.
procedure, pass(lhs), public :: add => add_lorenz !< Lorenz + Lorenz oprator.
procedure, pass(lhs), public :: assign_integrand => lorenz_assign_lorenz !< Lorenz = Lorenz.
procedure, pass(lhs), public :: assign_real => lorenz_assign_real !< Lorenz = real.
endtype lorenzThis Lorenz type embeds:
- the 5 parameters values;
- the Lorenz' state variable vector;
- 2 auxiliary (helper) methods, not detailed here they being of minor interest;
- all the
type_integranddeferred methods that are necessary for the definition of a valid concrete extension oftype_integrand.
We chose to define the Lorenz' state vector as a rank 2 array. In the first subscript there is the state space dimension, namely it has dimension equals to 3 containing the dependent state variables v1, v2, v3. In the second subscript are stored the current and the (eventually) previous time steps solution. The current time step solution is always the upper bound element of the second subscript. For example, let us consider to use a 2 time steps solver, the Lorenz' state vector has the following meaning:
-
lorenz%state(:, 1)=> solution at timen-1 -
lorenz%state(:, 2)=> solution at timen
It is worth to note that this definition allow us also to use a solver that involves only 1 time step, e.g. Runke-Kutta methods. In this case, the state array is allocated with only 1 time element that automatically corresponds to the upper bound of the second subscript. This is automatically accomplished by the init method.
The time derivative method lorenz%t => dLorenz_dt, namely the residuals function, depends only on the state vector at time step considered, thus it is very simple to implement:
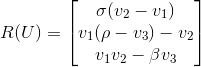
Using the above lorenz type definition it simply corresponds to:
pure function dLorenz_dt(self, n) result(dState_dt)
!---------------------------------------------------------------------------------------------------------------------------------
!< Time derivative of Lorenz field.
!---------------------------------------------------------------------------------------------------------------------------------
class(lorenz), intent(IN) :: self !< Lorenz field.
integer(I_P), optional, intent(IN) :: n !< Time level.
class(integrand), allocatable :: dState_dt !< Lorenz field time derivative.
type(lorenz), allocatable :: delta !< Delta state used as temporary variables.
integer :: dn !< Time level, dummy variable.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
! preparing temporary delta
allocate(delta)
delta%dims = self%dims
delta%steps = self%steps
allocate(delta%state(1:self%dims, 1:self%steps))
delta%sigma = self%sigma
delta%rho = self%rho
delta%beta = self%beta
! Lorenz equations
dn = self%steps ; if (present(n)) dn = n
delta%state(1, dn) = self%sigma * (self%state(2, dn) - self%state(1, dn))
delta%state(2, dn) = self%state(1, dn) * (self%rho - self%state(3, dn)) - self%state(2, dn)
delta%state(3, dn) = self%state(1, dn) * self%state(2, dn) - self%beta * self%state(3, dn)
call move_alloc(delta, dState_dt)
return
!---------------------------------------------------------------------------------------------------------------------------------
endfunction dLorenz_dtHere delta is our residuals values that is finally copied into the class(integrand) :: dState_dt returning variable. As you can see, the residuals implementation has a very-high level syntax that is easy understand and maintain.
For multi-step (level) time solver (like the Adams-Bashforth class) it is important to provide a method for update the previous time steps solution each time the current solution is integrated over one time step.
Using the above lorenz type definition it simply corresponds to:
pure subroutine update_previous_steps(self)
!---------------------------------------------------------------------------------------------------------------------------------
!< Update previous time steps.
!---------------------------------------------------------------------------------------------------------------------------------
class(lorenz), intent(INOUT) :: self !< Lorenz field.
integer :: s !< Time steps counter.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
do s=1, self%steps - 1
self%state(:, s) = self%state(:, s + 1)
enddo
return
!---------------------------------------------------------------------------------------------------------------------------------
endsubroutine update_previous_stepsIt a simple round-cycle that copy the solution of step n-s+1 into the n-s index, the solution of step n-s+2 into the n-s+1 index and so on until the current step n, s being the time steps used.
In the case you plan to not used multi-step solvers this method is not used, nevertheless it must be always implemented otherwise your Lorenz' definition is not a valid extension of the abstract type type_integrand. A simple implementation could be a do nothing method:
pure subroutine update_previous_steps(self)
!---------------------------------------------------------------------------------------------------------------------------------
!< FAKE update previous time steps for only non multi-step solvers.
!---------------------------------------------------------------------------------------------------------------------------------
class(lorenz), intent(INOUT) :: self !< Lorenz field.
!---------------------------------------------------------------------------------------------------------------------------------
!---------------------------------------------------------------------------------------------------------------------------------
return
!---------------------------------------------------------------------------------------------------------------------------------
endsubroutine update_previous_stepsODE solvers typically involve operation between your integrand field (the Lorenz' system here) and numbers (in general reals) and other integrand field instances. This means that you must implement an almost complete set of operators methods for performing summation, multiplication, division, etc... Here we not provide more details on these methods, the interested readers can see the tests suite sources.
Let us now assume to integrate the above Lorenz' system by means of the Adams-Bashforth-Schemes class of solvers. The steps to this aim are very few:
...
real(R_P), parameter :: sigma=10._R_P !< Lorenz' \(\sigma\).
real(R_P), parameter :: rho=28._R_P !< Lorenz' \(\rho\).
real(R_P), parameter :: beta=8._R_P/3._R_P !< Lorenz' \(\beta\).
real(R_P), parameter :: initial_state(1:3)=[1., 1., 1.] !< Initial state.
type(lorenz) :: attractor !< Lorenz field.
...
call attractor%init(initial_state=initial_state, sigma=sigma, rho=rho, beta=beta, steps=3)The Adams-Bashforth solvers class must be initialized selecting the time steps used:
...
type(adams_bashforth_integrator) :: ab_integrator !< Adams-Bashforth integrator.
...
call ab_integrator%init(steps=3)do while(.not.finished)
...
call ab_integrator%integrate(field=attractor, dt=0.01)
...
enddoFor a complete example see the Lorenz' test.