PDEs examples

In the PDEs category there are examples of integration of Initial Values Problems (IVP) mixed with Boundary Values Problems (IBP) where the integrand state is a function of time and space. The mathematical problem can be always formulated as

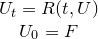
where:

• U_t = dU/dt;
• U is the vector of state variables being a function of the time-like independent variable t;
• R is the (vectorial) residual function;
• F is the (vectorial) initial conditions function.

In the PDEs category the time derivative residual function R is, in general, a function of U(t,x), x being the independent space vector field. In general, a PDEs system is re-conducted to an algebraic system of ODE by the application of the method of lines: the space operator if firstly discretized obtaining a semi-discrete form where the residual function is a system of algebraic equations.

The provided examples of PDEs integration are:

• Burgers' equation;
• 1D Euler's equations;