Skip to content

[statistics] Maximum Likelihood and Maximum Entropy

Jump to bottom
Myungchul Shin edited this page Mar 11, 2017 · 2 revisions

Conditional Density Estimation

model parameter estimation에서 아주 중요한 컨셉에 대해 설명한 자료라고 생각되어서 번역을 해볼까한다.(필요없는 부분은 스킵)

번역을 하기 전에, 우선 probability theory의 기본적인 용어(terminology)에 대해 알아보도록 하자.

사전지식

  • likelihood function
    likelihood function

    • 보면 알겠지만, likelihood는 P(X=x;θ)로 표현되는데 이것은 random variable X가 특정한 x일때 확률값이다. 여기서 θ는 어떤 모델 파라미터인데 probability distribution는 θ에 종속적(dependent)이다. 예를 들면, 동전던지기에서 앞면이 나올 확률값이 0.4라고 한다면 이것을 θ로 생각할 수 있다. 이 상태에서 동전이 앞면이 나온 결과 혹은 뒷면이 나온 결과에 대한 likelihood를 계산해보자.
      • L(θ|X=H) = P(X=H;θ) = 0.4, L(θ|X=T) = P(X=T;θ) = 0.6
        참 쉽죠잉
    • 위와 같이 observed sample 사이즈가 1일때가 아니라 n일때도 생각해보자.
      • sample이 X~P(X;θ)로부터 독립적으로(i.i.d) 생성되었다고 하면
      • L(θ|X=x1,X=x2,...,X=xn) = P(X=x1,X=x2,...,X=xn;θ) = Product{P(X=xi;θ)}
      • 이 형태는 NLP에서 매우 자주 등장한다. language model의 corpus 확률 혹은 sentence의 확률
    • 결국 likelihood는 random variable P(X;θ)로부터 생성된 sample 자체의 확률값이라고 볼 수 있다.

  • maximum likelihood

    • 앞에서 모델 파라미터 θ에 대해서 언급했었는데, θ값을 바꿀때마다 L(θ|X=x1,X=x2,...,X=xn)값도 변할 것이다. 그렇다면 어떤 θ가 더 좋은 것일까? likelihood는 [0,1] 사이의 값을 갖는 확률이므로 당연히 더 큰 값을 갖게 하는 θ가 좋다고 할 수 있다.(what θ makes sample data most likely?)
    • likelihood를 최대로 하는 θ를 찾는 방법이 바로 maximum likelihood estimation이다.

  • MLE for Bernoulli distribution

    • why sample mean is equal to maximum likelihood estimator in case Bernoulli distribution?
    • reference
    • Bernoulli distribution을 따르는 random variable X, 이 분포로부터 생성된(drawn) 사이즈가 n인 sample이 있다고 하자.
      • sample = { x1,x2,...,xn }
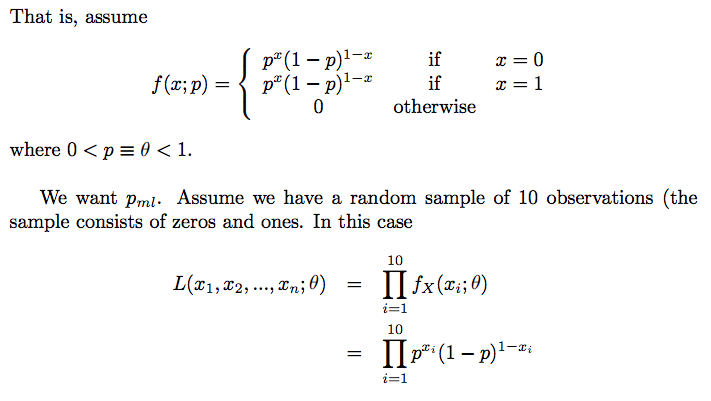
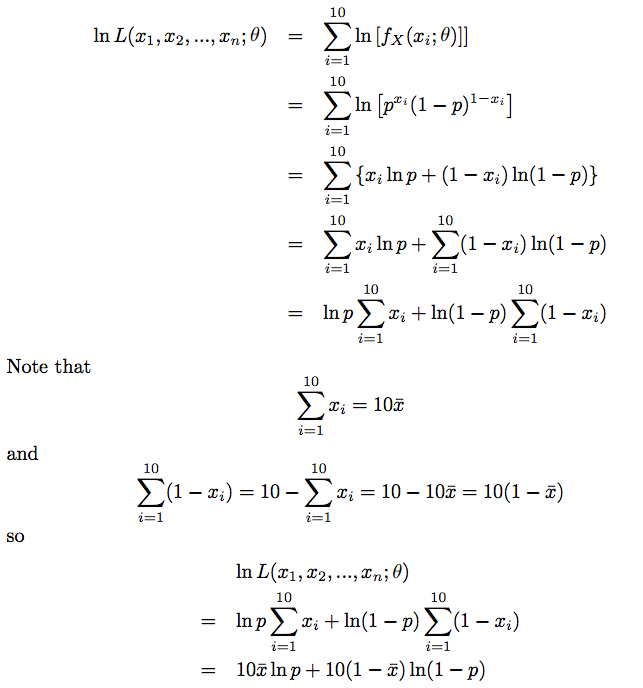
    • 이 sample로부터 Bernoulli distribution의 파라미터 θ=p (즉, success의 확률)를 추정해보자(estimation) Bernoulli estimation 1 Bernoulli estimation 2
    • likelihood는 보통 ln을 취해서 log likelihood로 계산하는데, 위 수식도 그러하다.
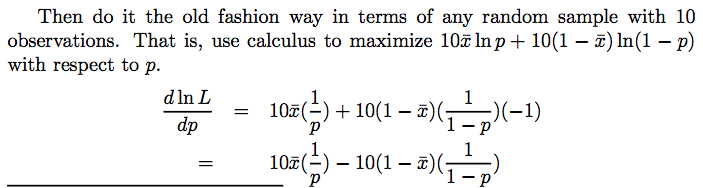
    • 위 수식에서 log likelihood가 최대가 되는 파라미터 p를 찾으면 되는데, 이것은 미분을 통해 해결할 수 있다. Bernoulli estimation 3 Bernoulli estimation 4
    • 따라서, θ=p=sample mean

  • MLE for binomial distribution

    • reference
    • Bernoulli distribution에서의 MLE 방법과 비슷하게 추정 가능하다.
    • binomial distribution을 따르는 random variable X, 이 분포로부터 생성된(drawn) 사이즈가 m인 sample이 있다고 하자.
      • sample = { x1,x2,...,xm }
    • 이 sample로부터 파라미터 θ=p (즉, success의 확률)를 추정해보자(estimation)
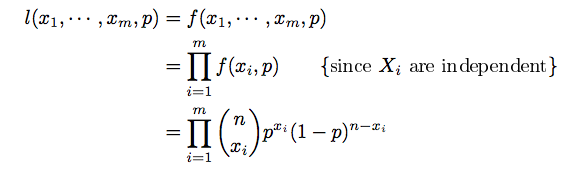
      binomial estimation 1
    • 양변에 로그를 취하면
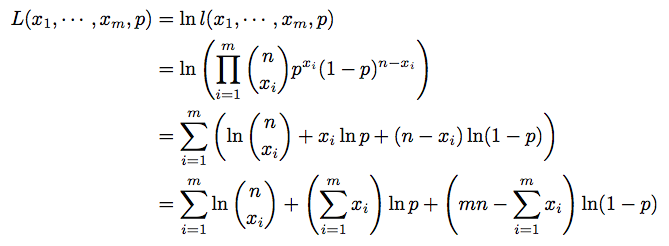
      binomial estimation 2
    • logarithm function은 monotonically increasing이므로 최대값이 존재한다. p에 대해 미분하면
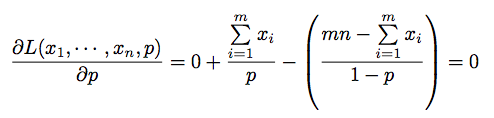
      binomial estimation 3
    • 수식을 정리하면
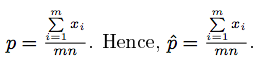
      binomial estimation 4
    • 이 결과를 잘 들여다보면, 결국 p는 sample로부터 계산된 success의 비율(proportion)과 정확히 같다는 것을 알 수 있다.
n = 7일때, 사이즈가 m인 ramdom sample이 아래와 같다고 하자. 

x1 = 1  '1000000' 
x2 = 4  '1010101'
...
xm = 7  '1111111'

여기서 p를 MLE방법으로 추정하면  

p' = (x1+x2+..+xm)/nm = (1+4+..+7)/7m

그런데, sample에서 1의 비율을 단순히 계산하면  
1의 개수 = x1 + x2 + ... + xm = 1+4+..+7
전체 개수 = n * m = 7m
따라서, 1의 비율 = (1+4+..+7)/7m = p'

  • MLE for multinomial distribution

    • reference
    • 앞에서 binomial distribution에 대한 파라미터 추정을 할때, size가 m인 샘플을 사용했었다. 하지만, 여기서는 size가 1이지만 매우 큰 n값을 갖는 sample이 하나 있다고 보고 계산해보자. category의 수는 k개.
      • multinomial distribution의 pmf은 아래와 같이 정의된다.
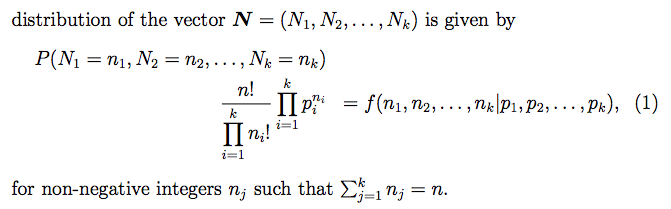
        multinomial estimation 1
      • sample의 사이즈가 1이므로, likelihood는 정확히 pmf과 같다.
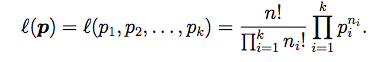
        multinomial estimation 2
      • 이 식을 최대화시키기는 parameter vector를 찾기 위해서는 앞서 binomial distribution에서 사용했던 방법을 그대로 사용할수는 없다. 왜냐하면 변수가 k개나 존재하고 각 변수끼리는 상호연관되어 있기 때문이다. 따라서, constraint optimization에서 자주 사용하는 Lagrange multiplier를 적용해본다. 그리고나서 좌변을 0으로 만드는 parameter vector를 편미변을 사용해서 찾는다. multinomial estimation 3
      • 여기에서도 비슷하게 추정된 pj 값은 sample에서 j의 상대 빈도수 혹은 비율(proportion)과 같다는 것을 알 수 있다.

  • maximum likelihood estimation for other distributions

번역

Summary. 이번 강의에서는 random sample(관측데이터)로부터 probability density function(pdf)을 추정하는 방법 대해 알아보기로 하자. 이러한 추정은 probability modeling 혹은 density estimation이라고도 하는데, 두가지 표준적인 방법인 maximum likelihood와 maximum entropy에 대해 소개한다.

Maximum Likelihood

x1,x2,...,xm example은 어떤 'distribution D over X'로부터 생성된 sample이라고 하자. 우리의 목표는 data에 가장 적합한(best fit) model을 찾는 것이다. 이런 문제는 풀때는 항상 model의 quality를 측정하는 어떤 measure가 필요한데, 바로 likelihood. likelihood of x1,x2,...,xm under q, log likelihood는 아래와 같이 정의된다.
ml 1
log likelihood가 최대가 되는 q를 찾는 문제는 수식 (3)을 최소화시키는 문제와 같다. 이것은 error라고 볼수 있기 때문에, 'log loss function'이라고도 부른다. 즉, log likelihood를 최대화시키는 것은 log loss를 최소화시키는 문제와 같다. ml 2
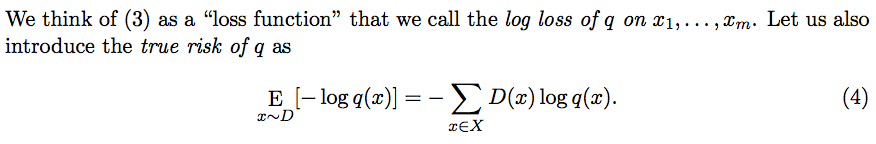
또한, 추정된 q가 있을 때, 이것과 실제 distribution D와의 차이를 true risk라고 부르는데, 이것은 수식 (4)와 같이 정의된다. ml 3
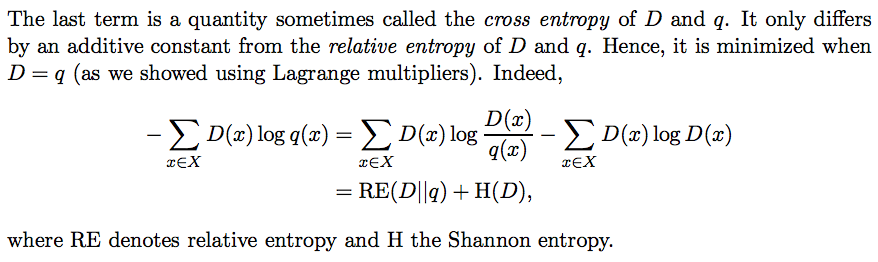
수식 (4)의 좌변은 cross entropy of D and q라고 부르는데, 위 수식과 같이 relative entropy와 entropy of D의 합으로 표현 가능하다. 직관적으로 이 수식이 최소값을 가지려면 'D=q'. 위 수식이 어째서 저렇게 되는지는 log의 성질을 이용해서 간단하게 증명 가능하다.

-log A = log 1/A = log (1/B) / (A/B) = log 1/B - log A/B = log B / A - log B

우리가 추정하려고 하는 q(x)는 xi를 n개의 feature function fj로 표현가능하다면 아래와 같이 exponential familiy로 만들 수 있다. 이 부분은 솔직히 잘 이해가 안됨
ml 4
따라서, q(x)를 위와 같이 표현할때 log likelihood를 최대화시키는 문제를 풀면 된다.

Maximum Entropy

앞에서와 같은 문제를 해결하는 또다른 접근방법은 maximum entropy. 이 방법은 기본적으로 아래와 같은 가정에서 출발한다. me 1

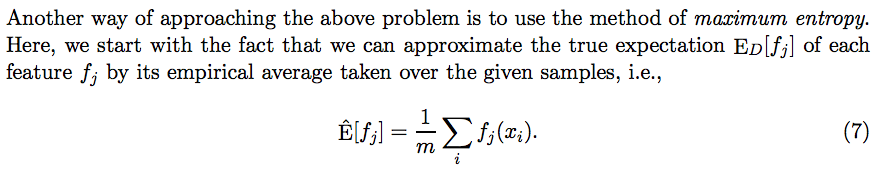
어떤 feature function fj에 대해서 sample에서 계산된 empirical everage는 true distribution D에서 계산된 fj의 expectation과 같다.

me 2

모든 j(j=1,2,...,n)에 대해서 수식 (8)을 만족하는 distribution p를 찾으면 되는데, 이런 p는 아주 많을 것이다. 이것들 중에서 uniform distribution과의 relative distance가 최소인 p를 찾으면 결국 H(p)를 최대화시키는 p를 찾는 문제와 같다. 따라서, 수식 (9)와 같이 표현할 수 있다.

Duality between Maximum Entropy and Maximum Likelihood

사실 maximum entropy는 maximum likelihood와 같은 '해'를 찾는다. du 1 즉, entropy를 최대화시키는 distribution p를 찾는 것과 log likelihood를 최대화시키는 distribution q를 찾는 것은 같은 문제인 것이다. 어째서 같은 문제인지는 아래와 같이 식을 전개하면 알 수 있다. du 2

Clone this wiki locally