Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
adding BetaBernoulli distribution with LogScore #132
base: master
Are you sure you want to change the base?
adding BetaBernoulli distribution with LogScore #132
Changes from 1 commit
98b5f94c30c64e98c9508ef7c60fFile filter
Filter by extension
Conversations
Jump to
There are no files selected for viewing
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
How did you derive this? In my derivation the Fisher Information is not diagonal.
Here's what I have; it'd be great if you could paste your independent derivation so that we can double check.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I made a mistake not including the other diagonal. My calculation was based on the definition of the FI matrix as the variance of the score. Therefore I just simply squared the gradient (but forgot that it's actually a vector and the square should be S*S.T).
Can we use the double derivative? Are we using this:
Claim: The negative expected Hessian of log likelihood is equal to the Fisher Information Matrix F.
https://wiseodd.github.io/techblog/2018/03/11/fisher-information/
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
As per my calculation the last row is different, it's
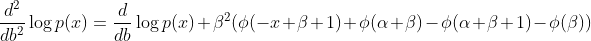
However when I use that formula the model doesn't work - it drops the singular matrix error again. And when I include the full FI matrix from the variance definition it also drops the singular matrix error. When I use the diagonal matrix from the Hessian definition it simply doesn't learn.
So the only working solution is the diagonal matrix from the variance definition. I have no clue why.
If you want to try the different approaches I have updated the code. All you need to do is to comment out the other diagonal or to comment out the other metric definition. For now I keep the working version as my pull request, but please check my code as I'm not sure I didn't miss something or didn't do a typo again.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Can we clean this function up a bit? In particular it's not clear what impressions / clicks are supposed to be. If
impressionsis going to be a vector of ones in all cases maybe we can remove it as an argument?Also it'd be great if we could apply
blackformatting.There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Cleared the function